Evolution will occur unless certain restrictive conditions exist
In 1908, the British mathematician Godfrey Hardy and the German physician Wilhelm Weinberg independently deduced the conditions that must prevail if the genetic structure of a population is to remain the same over time. If the conditions they identified do not exist, then evolution will occur. The resulting principle is known as Hardy–Weinberg equilibrium. Hardy–Weinberg equilibrium describes a model in which allele frequencies do not change across generations and genotype frequencies can be predicted from allele frequencies (Figure 20.11). The principles of Hardy–Weinberg equilibrium apply only to sexually reproducing organisms. Several conditions must be met for a population to be at Hardy–Weinberg equilibrium. Note that the following conditions correspond inversely to the five principal processes of evolution (discussed in Key Concept 20.2):
There is no mutation. The alleles present in the population do not change, and no new alleles are added to the gene pool.
There is no selection among genotypes. Individuals with different genotypes have equal probabilities of survival and equal rates of reproduction.
There is no gene flow. There is no movement of individuals into or out of the population or reproductive contact with other populations.
Population size is infinite. The larger a population, the smaller will be the effect of genetic drift.
Mating is random. Individuals do not preferentially choose mates with certain genotypes.
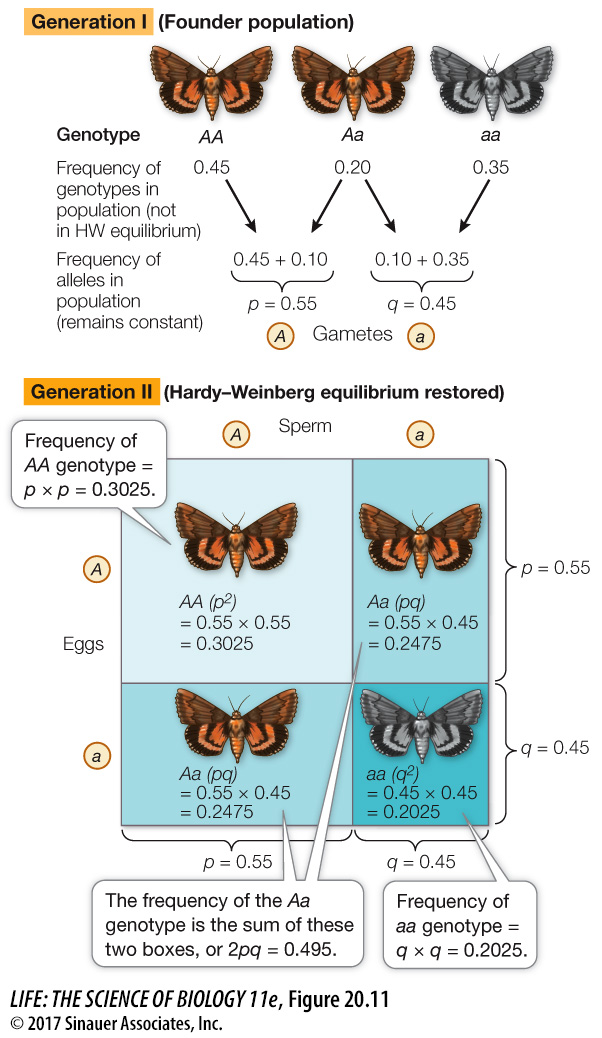
Figure 20.11 One Generation of Random Mating Restores Hardy–Weinberg Equilibrium Generation I of this population is made up of migrants from several source populations and so is not initially in Hardy–Weinberg equilibrium. After one generation of random mating, the allele frequencies are unchanged, and the genotype frequencies return to Hardy–Weinberg expectations. The lengths of the sides of each rectangle are proportional to the allele frequencies in the population; the areas of the rectangles are proportional to the genotype frequencies.
If these idealized conditions hold, two major consequences follow. First, the frequencies of alleles at a locus remain constant from generation to generation. Second, following one generation of random mating, the genotype frequencies occur in the following proportions:
Page 436
| Genotype |
AA |
Aa |
aa |
| Frequency |
p2
|
2pq |
q2
|
To understand why these consequences are important, start by considering a population that is not in Hardy–Weinberg equilibrium, such as generation I in Figure 20.11. This could occur, for example, if the initial population is founded by migrants from several other populations, thus violating the Hardy–Weinberg assumption of no gene flow. In this example, generation I has more homozygous individuals and fewer heterozygous individuals than would be expected under Hardy–Weinberg equilibrium (a condition known as heterozygote deficiency).
Even with a starting population that is not in Hardy–Weinberg equilibrium, we can predict that after a single generation of random mating, and if the other Hardy–Weinberg assumptions are not violated, the allele frequencies will remain unchanged, but the genotype frequencies will return to Hardy–Weinberg expectations. Let’s explore why this is true.
In generation I of Figure 20.11, the frequency of the A allele (p) is 0.55. Because we assume that individuals select mates at random, without regard to their genotype, gametes carrying A or a combine at random—that is, as predicted by the allele frequencies p and q. Thus in this example, the probability that a particular sperm or egg will bear an A allele is 0.55. In other words, 55 out of 100 randomly sampled sperm or eggs will bear an A allele. Because q = 1 – p, the probability that a sperm or egg will bear an a allele is 1 – 0.55 = 0.45.
To obtain the probability of two A-bearing gametes coming together at fertilization, we multiply the two independent probabilities of their occurrence:
p × p = p2 = (0.55)2 = 0.3025
Therefore 0.3025, or 30.25 percent, of the offspring in generation II will have homozygous genotype AA. Similarly, the probability of two a-bearing gametes coming together is
q × q = q2 = (0.45)2 = 0.2025
which means that 20.25 percent of generation II will have the aa genotype.
There are two ways of producing a heterozygote: an A sperm may combine with an a egg, the probability of which is p × q; or an a sperm may combine with an A egg, the probability of which is q × p. Consequently, the overall probability of obtaining a heterozygote is 2pq, or 0.495. The frequencies of the AA, Aa, and aa genotypes in generation II of Figure 20.11 now meet Hardy–Weinberg expectations, and the frequencies of the two alleles (p and q) have not changed from generation I.
Under the assumptions of Hardy–Weinberg equilibrium, allele frequencies p and q remain constant from generation to generation. If Hardy–Weinberg assumptions are violated and the genotype frequencies in the parental generation are altered (say, by the loss of a large number of AA individuals from the population), then the allele frequencies in the next generation will be altered. However, based on the new allele frequencies, another generation of random mating will be sufficient to restore the genotype frequencies to Hardy–Weinberg equilibrium.
Activity 20.4 Hardy–Weinberg Equilibrium
