Logistic growth occurs as a population approaches its carrying capacity
What would happen if all the offspring produced by a population survived and reproduced? The prospects are alarming. In 1911 L. O. Howard, then chief entomologist of the U.S. Department of Agriculture, estimated that if all the offspring of the common house fly (Musca domestica) were to survive, a pair of flies beginning to reproduce on April 15 would produce a population of 5,598,720,000,000 adults by September 10 of the same year. Given such amazing reproductive capacities, it is clear that forces exist to limit the growth of fly populations (and populations of every other organism).
No real population can maintain exponential growth for long periods of time. As a population increases in density, the resources it requires—
focus: key figure
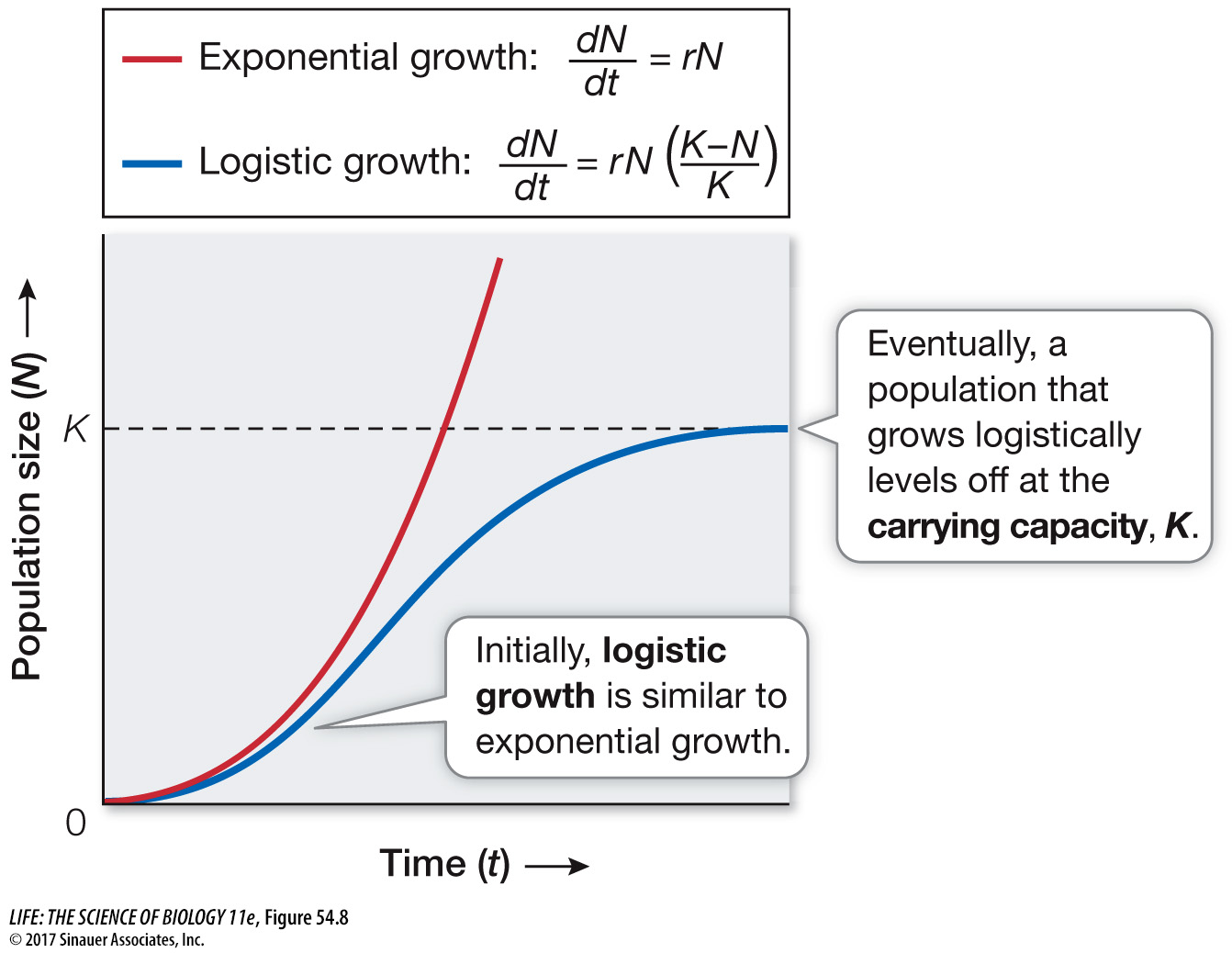
Q: How does exponential growth differ from logistic growth?
Exponential growth occurs when the rate of change in population size is multiplicative but constant over time. Logistic growth occurs when resources are limited and intraspecific competition slows growth of the population to its maximum size (carrying capacity).
Activity 54.3 Logistic Population Growth Simulation
To model logistic growth, the exponential growth equation is modified by adding a term, (K – N0)/K, which represents the fraction of the carrying capacity (K) that is available for population growth. As long as the population size is less than the carrying capacity (i.e., N0 < K), only a fraction of the available resources are being used. As the population size approaches the carrying capacity, however, the fraction of resources available for any new individual becomes smaller. The logistic growth equation is simply the exponential growth rate rN0 multiplied by (K – N0)/K to get

Population growth should stop when N0 = K because at that point, K – N0 = 0, so (K – N0)/K = 0, and thus dN/dt = 0 and the population will remain at a constant size.
Just as you saw with Equation 54.5, we can integrate Equation 54.6 to allow us to predict the population size at some later time, assuming logistic growth. When we do this we get
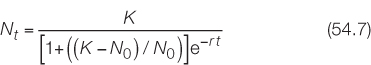
where Nt = the population size at time t, N0 = the population size at time 0, e = a constant, the base of the natural log (e = 2.718), r = per capita growth rate, K = carrying capacity, and t = the time interval between time 0 and time t. In this case, knowing the starting population size, the per capita growth rate, and the carrying capacity of the population, we can use Equation 54.7 to forecast population size at some later time, assuming logistic growth.
Activity 54.2 Population Growth