Logarithms

Logarithms can be used to solve problems involving exponential functions, such as the half-life of a radioactive substance or the pH of a solution.

A logarithm is an exponent and is abbreviated log. For example, log10 x is the exponent you put on 10 to get x. So, if x = 100, then log10 x = 2 because 102 = 100. In the same way, log10 1000 = 3, log10 10 = 1, 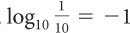image . Ten is a common base for logarithms, so log x is called a common logarithm and is shorthand for log10x. Check out these log equivalents on your calculator, and use your calculator to determine the logs of numbers that are not multiples of 10.

A-18

Because logarithms are exponents, they follow the properties of exponents.

Product property am · an = am+n log xy = log x + log y
Quotient property am/an = am–n log x/y = log x – log y
Power property log xn = n log x

In some problems you know what the logarithm is, but you want to find the number that has that logarithm. What you are looking for is called the antilogarithm, abbreviated antilog. Use the 10x key on your calculator to find an antilog.

Example 1

Comparing Logarithms

Find the values a–f. Which values are equal?

a = log 18 b = log 71 c = a + b d = antilog c e = 18 · 71 f = log(8 · 71)

Solution

a ≈ 1.255; b ≈ 1.851; c ≈ 3.106; d = 1278; e = 1278; f ≈ 3.106

d = e, or antilog (log 18 + log 71) = 18 · 71

c = f, or log 18 + log 71 = log (8 · 71)

Example 2

pH

What is the pH of a solution in which [H1] is 5.3 × 10−4?

Solution

Start with the definition of pH.

pH = –log [H+]
Substitute the value of [H1]. = –log [ 5.3 × 10–4]
Find the log, then change the sign. = 3.3 5

Practice Exercises

  1. Find the log.

    1. 456

    2. image

    3. 3.4 × 10–6

  2. Find the antilog

    1. 2

    2. –3

    3. 3.4

  3. The pH of a solution is 8.2 5. What is the concentration of hydrogen ions in the solution?

Show Answers

Answers

1a. 2.659 1b. log x – 1.176 1c. 5.469
2a. 100 2b. 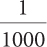image 2c. 2512 3. 5.62 × 10–9