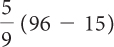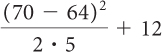Order of Operations
Math expressions and equations often involve several operations. For example, to convert from Celsius to Fahrenheit, you first multiply the number of Celsius degrees by the fraction  and then add 32 degrees. To convert from Fahrenheit to Celsius, you subtract 32 degrees from the number of Fahrenheit degrees and then multiply the result by
and then add 32 degrees. To convert from Fahrenheit to Celsius, you subtract 32 degrees from the number of Fahrenheit degrees and then multiply the result by  . A rule called the order of operations is used to write math expressions clearly so that anyone seeing the formula or equation would know whether multiplication was the first step or the second step.
. A rule called the order of operations is used to write math expressions clearly so that anyone seeing the formula or equation would know whether multiplication was the first step or the second step.
Order of Operations
Evaluate all expressions within parentheses.
Evaluate all terms with exponents.
Multiply and divide from left to right.
Add and subtract from left to right.
Example 1
Temperature Conversions
Convert these temperatures.
37 °C to degrees Fahrenheit
48 °F to degrees Celsius
Solution
Substitute the known value into each equation and then solve using the order of operations.
| a. Substitute 37° into the equation. |
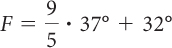
|
| Multiply. | F = 66° + 32° |
| Add. | F = 98 °F |
| b. Substitute 48° into the equation. |

|
| Subtract. |
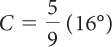
|
| Multiply. | C = 9 °C |
Example 2
Parentheses, Exponents, and Fractions
Evaluate these expressions.
Solution
Evaluate the expression in the parentheses first.
| a. Original expression |
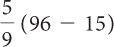
|
| Subtract the numbers within the parentheses. |
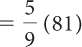
|
Multiply  by 81.
by 81. |
= 45 |
b. The fraction line acts like parentheses. In fact, when the expression is entered into a calculator, parentheses are required around the 2 · 5.
| Original expression. |
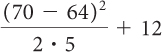
|
| Evaluate the expressions above and below the fraction line. |
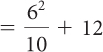
|
| Divide 36 by 10 and then add 12. | = 15.6 |
Practice Exercises
Evaluate these expressions.
3 · 24 ÷ 8
3 + 24 · 8
3 – 24 + 8
(3 + 24) · 8
(3 + 21) ÷ 8
3 – (24 + 8)
Calculate the value of each expression.
–2 + 5– (–8)
(– 52) – (–3)2
–0.3 · 20 + 15
Insert parentheses as needed to make each equation true.
1 5 ÷ 3 + 7 – 4 = –48
1 5 ÷ 3 + 7 – 4 = 8
–42 + –32 = –7
Answers
1a. 9
1b. 195
1c. –13
1d. 216
1e. 3
1f. –29
2a. 11
2b. –34
2c. 9
3a. (15 ÷ 3 + 7)(–4) = –48
3b. 15 ÷ 3 + 7 – 4 = 8
3c. –42 + (–3)2 = –7