More Stoichiometry Practice

Recall from Unit 4: Toxins that stoichiometry involves calculations based on the quantitative relationship between amounts of reactants and products in a chemical reaction. Using mole ratios from a balanced chemical equation, it’s possible to determine amounts of reactants and products that will be used or formed during a reaction.

When the calculations involve amounts in mass, you need to convert given amounts in mass to moles. To do this, you use the molar mass for each substance, because the molar mass is the amount in grams of exactly one mole of that substance.

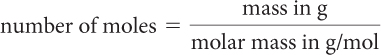
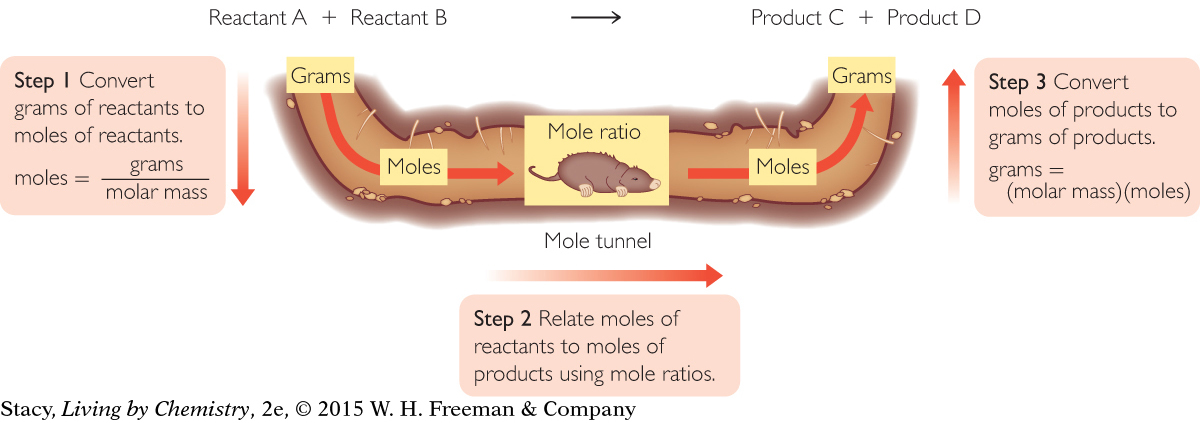
image

Once you convert amounts to moles, you can use mole ratios from the balanced chemical equation to relate reactants to products. The “mole tunnel” is a way to help you remember these steps.

image

B-18

If you are solving a problem that involves a particular volume of gas, you also need to convert to moles. Recall from Unit 3: Weather that at standard temperature and pressure, STP, one mole of gas occupies a volume of 22.4 liters.

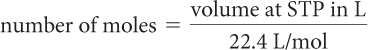
image

If the reaction is not carried out under STP conditions, you can use the ideal gas law, PV = nRT, to solve for the number of moles, n, as long as you are given the temperature, volume, and pressure.

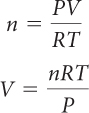
image

In the above equations, the number of moles is represented by n, pressure by P, volume by V, temperature by T, and R is the ideal gas constant.

It is also possible to solve stoichiometry problems in terms of the numbers of particles of each substance because one mole of a substance = 6.02 × 1023 particles (such as atoms, molecules, ions, or formula units).

number of particles 5 6.02 3 1023 particles/mol . (number of moles)

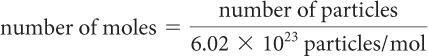
image

Example 1

Volume of Gas Produced in a Reaction at STP

What volume of H2O vapor is produced when 0.35 mol of O2 gas reacts with an excess of H2 gas at STP? How many molecules of H2O is this?

Solution

Step 1: Write the balanced equation for this reaction.

2H2(g) + O2(g) → 2H2O(g)

Step 2:The oxygen gas, O2, is already reported in moles. There is an excess of hydrogen, H2, so oxygen, O2, is the limiting reactant. Use mole ratios to determine the amount of product in moles.

The mole ratio of O2 to H2O is 1:2.

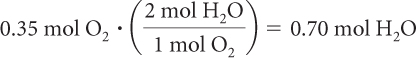
image

So 0.70 mole of H2O(g) is produced in this reaction.

Step 3: Convert moles of H2O(g) to volume of H2O(g). This reaction takes place at standard temperature and pressure, STP.

B-19

volume of H2O at STP = number of moles · (22.4 L/mol)

volume of H2O at STP = 0.70 mol H2O · (22.4 L/mol)

volume of H2O at STP = 15.68 L, rounded to two significant figures, 16 L

Step 4: Convert moles of H2O (g) to number of molecules.

number of molecules H2O = 6.02 × 1023 particles/mol · (number of moles)

number of molecules H2O = 6.02 × 1023 particles/mol · (0.70 mol H2O)

= 4.21 3 1023 molecules H2O, rounded to two

significant figures, 4.2 × 1023 molecules H2O

Recall from Unit 3: Weather that if there is a mixture of nonreacting gases, the pressure exerted by one gas in the mixture is called the partial pressure. Dalton’s law of partial pressures states that the partial pressures of all the gases add up to the total pressure exerted by that mixture of gases. This information can also be helpful in solving stoichiometry problems involving gases.

Dalton’s Law of Partial Pressures

P total = P1 + P2 + P3...

In the above equation, the numbered subscripts refer to each individual gas in the mixture.

Example 2

Stoichiometry with Partial Pressures and the Ideal Gas Law

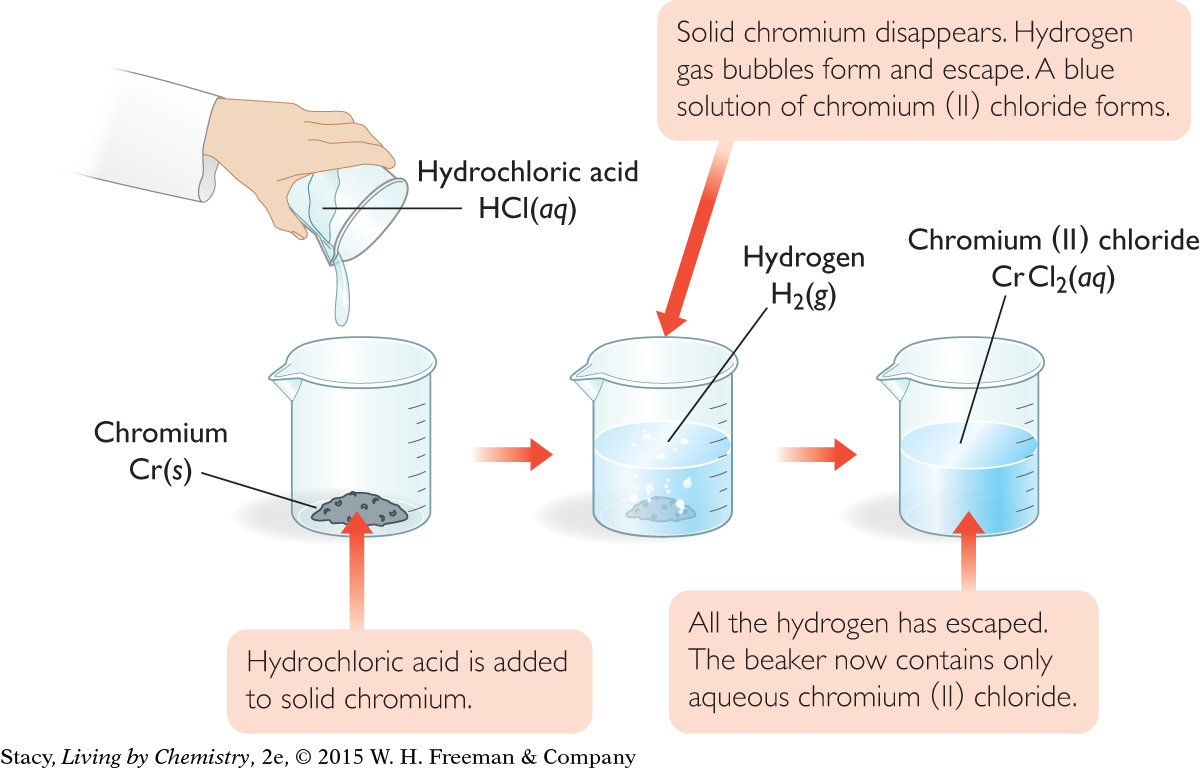
A student carried out the experiment from the illustration with an excess of hydrochloric acid. The student added a step to bubble the hydrogen gas formed through a closed container of water to collect it in the space above the water. When finished, a 75 mL mixture of water vapor and hydrogen gas was above the water. If the temperature in the container was 30 °C, the total pressure of the gas mixture was 1.015 atm, and the pressure of water vapor was 0.042 atm, what mass of chromium must have reacted?

image

Solution

Step 1: Start by writing the balanced chemical equation for the reaction.

B-20

Cr(s) + 2HCl(aq) → H2(g) + CrCl2(aq)

Step 2: To determine the mass of chromium reacted, you need to determine how much hydrogen gas was formed. The problem states the total pressure of the final mixture of gas, the total volume of the mixture of gas, and the partial pressure of water vapor under these conditions. You can use Dalton’s law of partial pressures to determine the pressure of the hydrogen gas in the mixture and then the ideal gas law to determine the amount of hydrogen in moles.

Ptotal = PH2O + PH2

PH2= Ptotal – PH2O

PH2= 1.015 atm – 0.042 atm

PH2= 0.973 atm

Step 3: Use the ideal gas law to calculate the number of moles of hydrogen gas produced.

T = 30 °C + 273 = 303 K

75 mL = 0.075 L

image

=2.9×10–3 mol H2

Step 4: Use mole ratios to work backward to determine the number of moles of chromium that reacted.

The mole ratio of Cr to H2 is 1:1

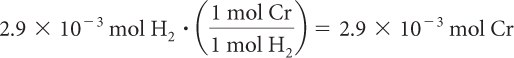
image

Step 5: Convert moles of Cr to grams.

mass of Cr = (52.00 g/mol).(2.9×10–3 mol)

=0.15 g Cr

BASIC STEPS FOR SOLVING STOICHIOMETRY PROBLEMS

In general, you can follow some basic steps to solve stoichiometry problems.

  1. If not given, write a balanced chemical equation.

  2. Convert amounts given in mass, volume, or number of particles to moles.

  3. If needed, determine the limiting reactant using mole ratios.

  4. Use mole ratios to relate reactants to products.

  5. Convert amounts in moles back to mass, volume, or number of particles.

Sometimes, you have to incorporate other chemistry concepts, as in Example 2, before you can solve the problem. So before you begin each problem, determine:

B-21

Practice Exercises

  1. Using the balanced equation from Example 1, determine the volume of O2 gas required to produce 5.50 moles of H2O vapor at STP.

  2. Consider this balanced chemical equation.

    B-22

    2C2H2(g) + 5O2(g) → 4CO2(g) + 2H2O(g)

    1. Find the mole ratio of C2H2 to O2.

    2. Find the mole ratio of C2H2 to CO2.

    3. Suppose you have 2.0 L of ethyne, C2H2. What volume of oxygen gas would be needed to react completely with 2.0 L of ethyne at STP?

    4. What volume of carbon dioxide would be produced from 2.0 L of ethyne at STP?

  3. Consider this balanced chemical equation.

    Mg(s) + 2HCl(aq) → MgCl2(aq) +H2 (g)

    A 120 mL sample of hydrogen gas was collected over water at 24³ C. The vapor pressure of water at 24 ?C is 0.030 atm. The total pressure of gas collected was 1.010 atm. What mass of magnesium must have reacted to produce this amount of hydrogen gas with excess hydrochloric acid?

  4. Consider this balanced chemical equation.

    2KClO3(s) → 2KCl(s) + 3O2(g)

    1. How many moles of KClO3 are needed to produce 0.60 mol of O2?

    2. What mass of KClO3 is needed to produce 0.20 mol of KCl?

    3. How many molecules of O2 are produced from 0.50 mol KClO3?

  5. Consider this balanced chemical equation.

    2Mg(s) + O2(g) → 2MgO(s)

    1. What volume of oxygen gas is needed to burn 0.50 g of magnesium ribbon at STP?

    2. What mass of MgO will be produced from the 0.50 g magnesium ribbon?

  6. Consider this balanced chemical equation.

    4Al(s) + 3O2(g) → 2Al2O3(s)

    What mass of aluminum would be used in the production of 10.2 g of aluminum oxide if aluminum reacted directly with unlimited oxygen?

  7. Consider this balanced chemical equation.

    C(s) + O2(g) → CO2(g)

    1. If 6.00 g of carbon were burned to form CO2, what mass of CO2 would be expected?

    2. If the actual yield of CO2 was measured to be 19.0 g, what is the percent yield?

  8. Consider this balanced chemical equation.

    CH4(g) + 2O2(g) → CO2(g) + 2H2O(g)

    1. If 50.0 g of methane, CH4, were burned, what mass of CO2 would be expected?

    2. If the actual yield of CO2 was measured to be 98.0 g, what is the percent yield?

  9. Consider this balanced chemical equation.

    3Fe(s) + 4H2O(g) → Fe3O4(s) + 4H2(g)

    1. How many moles of Fe3O4 can be obtained by reacting 16.8 g Fe with 10.0 g H2O?

    2. Which substance is the limiting reactant?

    3. Which substance is in excess?

  10. The following reaction was performed with 36.0 g Mg and 0.25 L of a 2.0 M HCl.

    Mg(s) + 2HCl(aq) →MgCl2(aq) + H2(g)

    1. Which compound is the limiting reactant?

    2. What mass of hydrogen gas was produced?

    3. What mass of magnesium chloride was produced?

Show Answers

Answers

  1. 1. 61.6 L O2

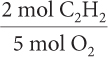
  2. 2a. image

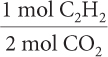
  3. 2b. image

  4. 2c. 5.0 LO2

  5. 2d. 4.0 L CO2

  6. 3. 0.12 g Mg

  7. 4a. 0.40 mol KClO3

  8. 4b. 24.5 g KClO3

  9. 4c. 4.52 × 1023 molecules O2

  10. 5a. 0.23 L O2

  11. 5b. 0.83 g MgO

  12. 6. 5.40 g Al

  13. 7a. 22.0 g CO2

  14. 7b. 86.4%

  15. 8a. 137 g CO2

  16. 8b. 71.5%

  17. 9a. 0.100 mol Fe3O4

  18. 9b. iron, Fe

  19. 9c. water, H2O, is in excess

  20. 10a. HCl

  21. 10b. 0.50 g H2

  22. 10c. 23.8 g MgCl2, rounded to two significant figures, 24 g MgCl2