LESSON 59: Egg in a Bottle
309
THINK ABOUT IT
Gases are trapped in balloons, soda cans, pickle jars, bicycle tires, and in your lungs if you hold your breath. Some of these containers are flexible and can vary in size, while others are rigid. A gas sample can be described by pressure, volume, and temperature. The gas might be heated, cooled, compressed, taken underwater, left outside overnight, or taken up in an airplane.
How does gas pressure change in flexible and rigid containers?
To answer this question, you will explore
Gay-Lussac’s Law
Gas Law Problems
Gay-Lussac’s Law
EXPLORING THE TOPIC
Gay-Lussac’s Law

Gases are sometimes stored in rigid gas containers. For example, underwater divers wear a metal gas tank strapped to their backs. To supply air to the diver for a sufficient amount of time, a lot of air is pushed or compressed into the tank. The result is that the gas inside the tank is at a high pressure.
With rigid containers the pressure of the air inside the container changes if the temperature changes. Indeed, there is a risk of an explosion if you heat the gas inside a pressurized tank.
PRESSURE VERSUS TEMPERATURE
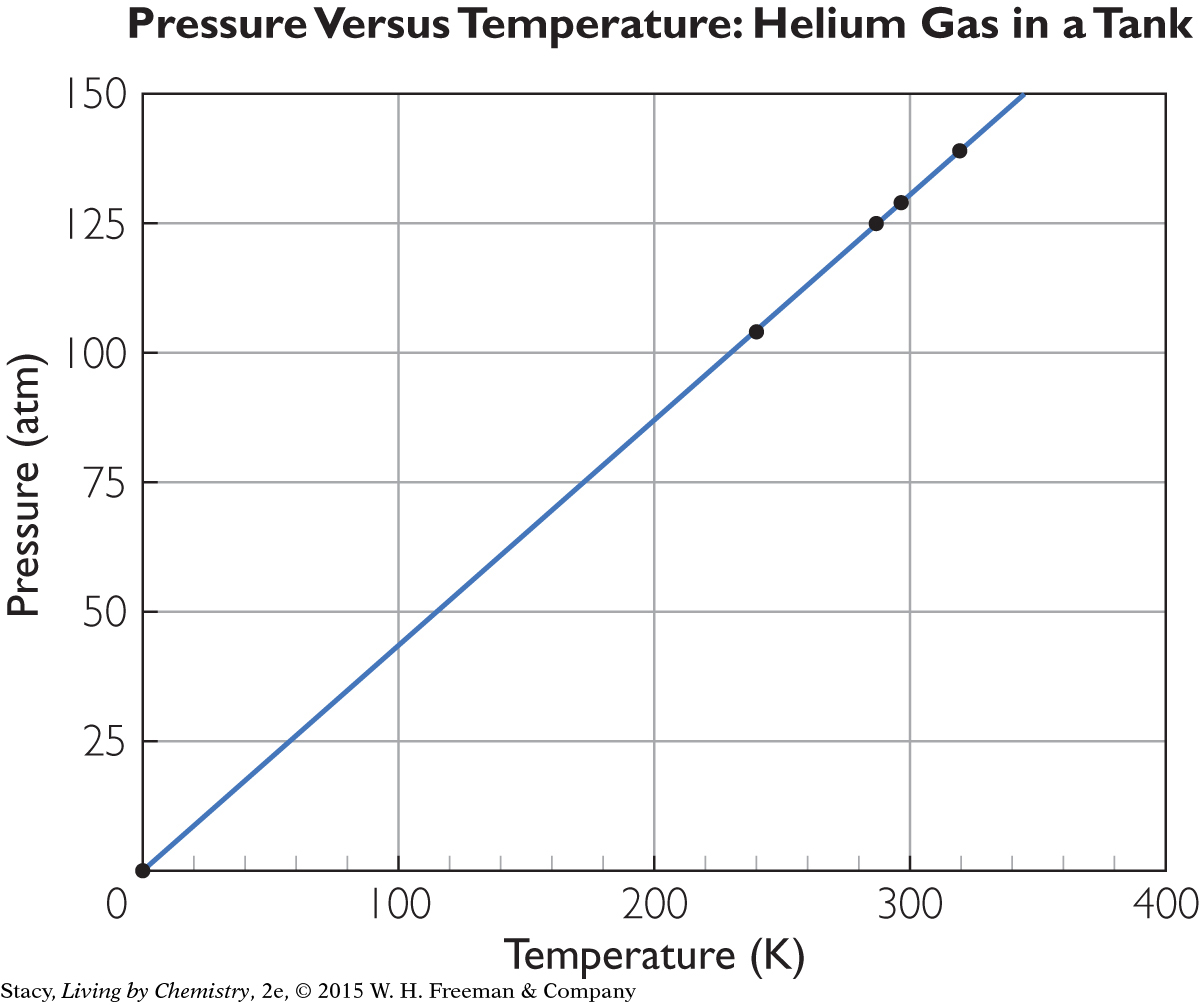
Consider a tank containing helium. If this tank is placed in the sun and the temperature increases, the pressure of the gas inside the tank also increases.

COOKING CONNECTION
COOKING
CONNECTION
A pressure cooker can cook food in a fraction of the time it takes with a regular pot. Because the lid fits tightly, a higher pressure is achieved, resulting in a higher temperature.

310
Big Idea
Big Idea
If you heat a sample of gas in a closed rigid container, its pressure will increase.
If you graph the helium tank data, the points lie on a straight line. The straight line through the data points and the point (0, 0) indicate that there is a proportional relationship between pressure and temperature. Joseph Louis Gay-Lussac, a French scientist, described this proportional relationship in the early 1800s.
Gay-Lussac’s Law The pressure P and the Kelvin temperature T of a gas are proportional when the volume and the amount of gas do not change. The relationship is P = kT. The value of the proportionality constant, k, depends on the specific gas sample.
Example 1
Propane Gas Tank
A 5.0 L propane gas tank on a camping stove contains propane gas at a pressure of 2.0 atm when the temperature is 14 °C (about 57 °F) in the morning. During the day, the tank warms up to a temperature of 34 °C (about 93 °F). What is the pressure of the propane gas inside the tank when the gas temperature is 34 °C?
Solution
The volume of the tank does not change. The temperature of the gas increases, causing the pressure of the gas to increase.
You can use the subscript 1 for the first set of conditions, and subscript 2 for the second set of conditions. These are sometimes called initial conditions and final conditions. You need to find P2, the final pressure.

The variables that are changing are P and T. Use Gay-Lussac’s law: P = kT. Recall that the temperature must be in kelvins.
| Convert the temperature to the Kelvin scale. | K = 273 + C T1 = 273 + 14 = 287 K (in the morning) T2 = 273 + 34 = 307 K (during the day) |
| Determine the value of k using P1 and T1. |
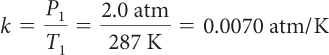
|
| Use k to solve for P2. |
P2 = k T2 = 0.0070 atm/K · 307 K = 2.15 atm |
At 34 °C, the pressure of the propane gas in the tank has increased to 2.15 atm.
Gas Law Problems
Gas Law Problems
311
SPORTS CONNECTION
SPORTS
CONNECTION
The tire pressure of race cars is extremely important. If the tire pressure is too high, the tires won’t have enough contact with the track. If the tire pressure is too low, the cars won’t handle well. But the tires heat up considerably during a race, increasing the pressure. The average temperature of a tire being removed during a pit stop is about 100 °C.

Gas pressure, gas volume, and gas temperature can change depending on the conditions. But no matter what, the gases must obey the gas laws!
There are two general types of containers: rigid and flexible. A rigid container has a volume that doesn’t change. A flexible container can vary in size.
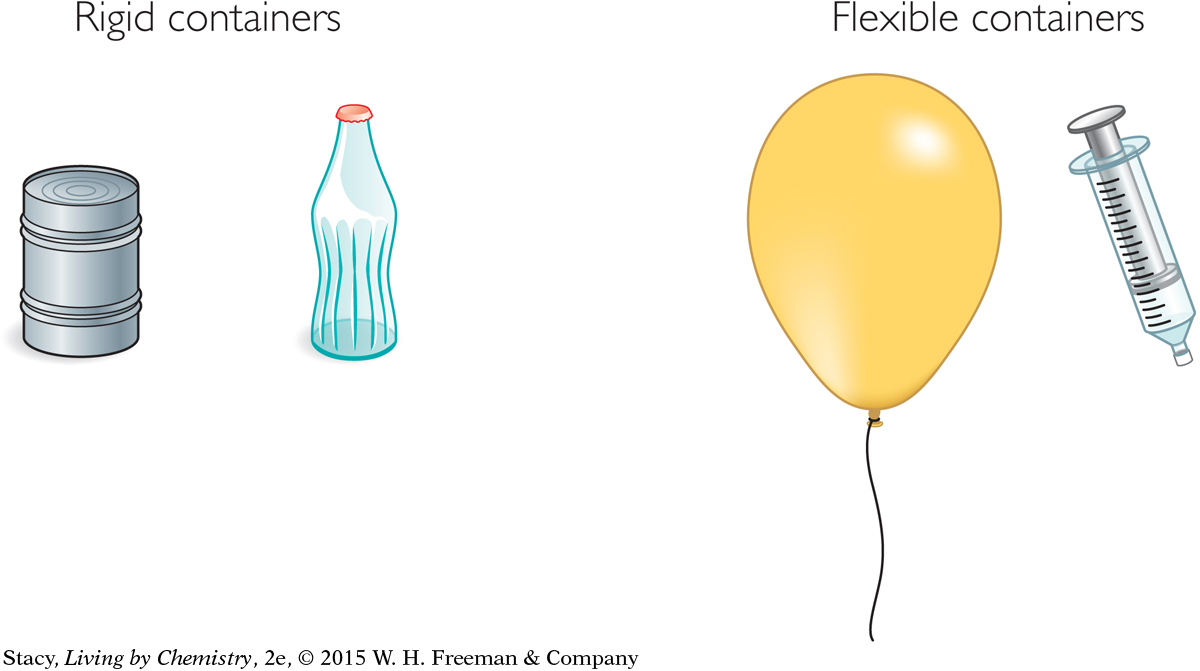
The type of container has an effect on what happens to the gas inside when the conditions change. For example, Boyle’s law and Charles’s law apply when a gas sample is in a flexible container, which can change volume. Gay-Lussac’s law applies for gas samples in rigid containers.
312
Important to Know
All temperatures must be converted to the Kelvin scale when completing gas law problems.
So far you’ve been introduced to three of the gas laws. These gas laws apply when any two of the variables, P, V, or T, are changed and everything else stays the same.
| Charles’s law | V = kT | P and amount of gas do not change. | 
|
| Gay-Lussac’s law | P = kT | V and amount of gas do not change. | 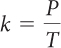
|
| Boyle’s law | 
|
T and amount of gas do not change. | k = PV |
Note that the proportionality constant, k, is a generic symbol and is different for each gas sample and for each gas law.
Example 2
Balloon with Air
Imagine that you fill a balloon with air to a volume of 1.5 L. The air is at a temperature of 20 °C. You place the balloon in a refrigerator for half an hour until the air in the balloon is at a temperature of 10 °C. What is the new volume of the balloon?
Solution
First figure out which gas law to use. The external pressure on the balloon remains the same because the air pressure in the refrigerator is the same as the air pressure outside. Use Charles’s law. You can predict that V will decrease because T decreases.

| Convert temperature to the Kelvin scale. | K = 273 + C T1 = 273 + 20 = 293 K T2 = 273 + 10 = 283 K |
| Determine the value of k. |
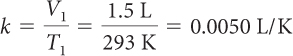
|
| Use k to determine V2. |
V2 = k T2 = 0.0050 L/K · 283 K = 1.4 L |
The balloon has shrunk to a volume of 1.4 L.
LESSON SUMMARY
LESSON SUMMARY
How does gas pressure change in flexible and rigid containers?
KEY TERM
Gay-Lussac’s law
313
Gases can be trapped in an assortment of containers and subjected to various conditions of pressure, temperature, and volume. The gas laws allow you to calculate new values for gas temperature, gas pressure, and gas volume when two of these three variables change while the other remains the same. Charles’s law and Gay-Lussac’s law are proportional relationships: V = kT and P = kT. Boyle’s law is different because P and V are inversely proportional: P = k(1/V). The proportionality constant, k, is the key to solving gas law problems.
Exercises
Reading Questions
Describe three ways in which you can change a gas sample.
Explain the difference between flexible and rigid containers.
Reason and Apply
A scuba-diving tank holds 18 L of air at a pressure of 40 atm. If the temperature does not change, what volume would this same air occupy if it were allowed to expand until it reached a pressure of 1.0 atm?
Imagine you fill a balloon with air to a volume of 240 mL. Initially, the air temperature is 25 °C and the air pressure is 1.0 atm. You carry the balloon with you up a mountain where the air pressure is 0.75 atm and the temperature is 25 °C.
When the balloon is carried up the mountain, what changes? What stays the same?
The air pressure on the outside of the balloon has decreased. Can the air pressure on the inside decrease so that the pressures are equal? Why or why not?
What happens to the volume occupied by the air inside the balloon? Explain your thinking.
Solve for the new volume of the balloon.
The air inside a 180 mL glass bottle is at 1.0 atm and 25 °C when you close it. You carry the glass bottle with you up a mountain where the air pressure is 0.75 atm and the temperature is 5 °C.
The air pressure on the outside of the glass bottle has decreased. What happens to the volume of air inside of the bottle? Explain your thinking.
Do you expect the temperature of the air inside the bottle to cool to 5 °C when you’re at the top of the mountain? Explain your thinking.
What happens to the pressure inside the glass bottle? Explain your thinking.
Solve for the new pressure of the gas.