LESSON 97: Heat versus Temperature
THINK ABOUT IT
Imagine that you want two samples of really hot water. You want a large sample to make soup and a smaller sample for a cup of hot cocoa. Will it take the same amount of heat to get both samples to the same temperature?
What is the difference between temperature and heat?
To answer this question, you will explore
Particle View of Energy
Measuring Heat Transfer
Particle View of Energy
EXPLORING THE TOPIC
Particle View of Energy
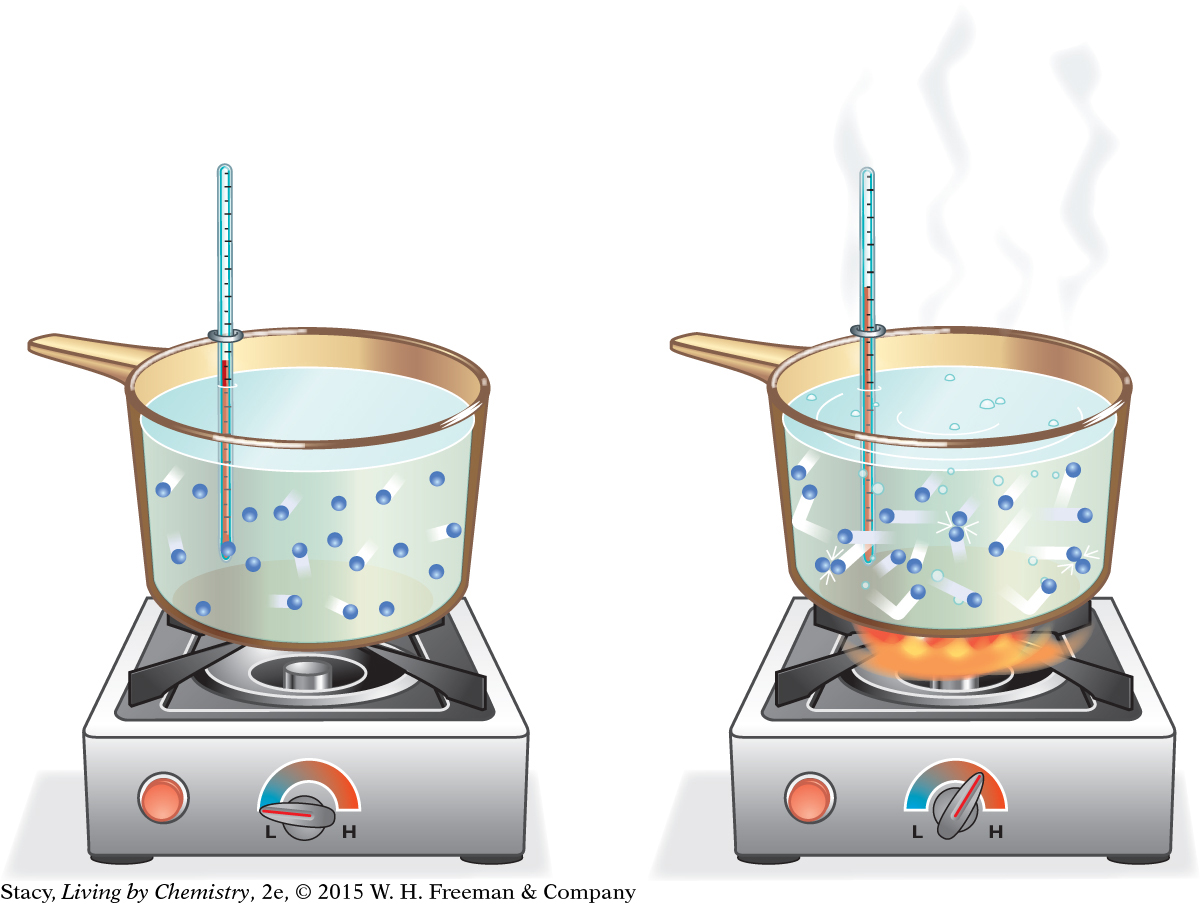
Consider a sample of water molecules that is heated. What happens to the molecules as more energy is transferred to the sample?
As shown in the illustration (left), atoms and molecules move faster as they are heated. As the movement of the molecules increases, the temperature of the sample goes up.
Now consider two samples of water that contain different numbers of molecules. While the temperatures might be identical, the amount of energy represented by the two samples is not the same. In one sample, you have many quickly moving particles. In the other sample, you have fewer particles, even though they are moving just as quickly. There will be more total energy in the larger sample.
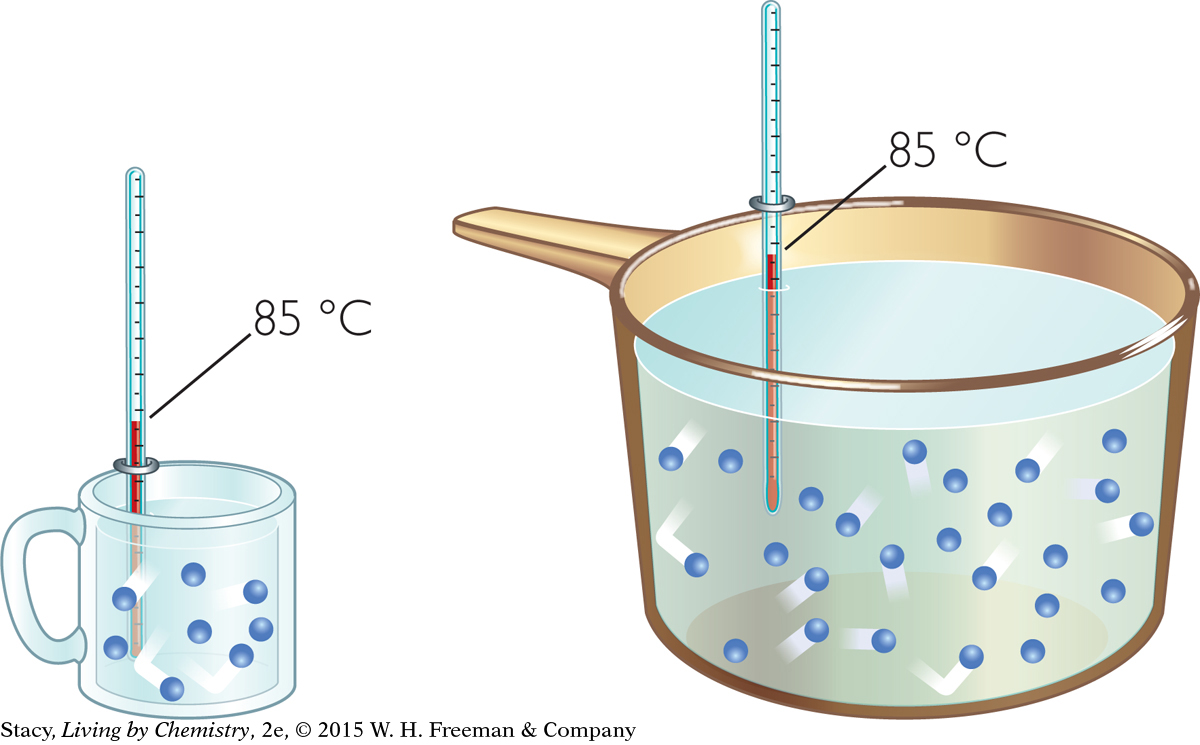
If the water samples in the large pot and the small cup shown in the illustration (bottom left) are both at 85 ºC, you could say that they both have the same “degree of hotness,” or temperature. However, the water in the large pot has a greater total “quantity of hotness” because it is a larger sample. This second concept is referred to as thermal energy. Thermal energy describes the total amount of energy in the particles of a sample. Because the temperature is the same, the gas molecules in both samples are moving with the same average kinetic energy. Because their volumes are different, the two samples have different amounts of thermal energy. So thermal energy is dependent on both the temperature of the sample and on the number of particles in the sample.
Big Idea
Big Idea
Temperature depends on the average kinetic energy of matter. Thermal energy depends on the average kinetic energy and the mass of the sample.
Measuring Heat Transfer
Measuring Heat Transfer
Unfortunately, you cannot measure the thermal energy of a sample of matter directly. A thermometer gives you only an indication of the average kinetic energy. However, changes in thermal energy can be determined using heat transfer.
Imagine that you have three samples of water at different temperatures: a pitcher of water at 80 ºC, a beaker of water at 80 ºC, and a pitcher of water at 50 ºC. Your common sense tells you that the largest 80 ºC sample is the one with the greatest thermal energy. But can that energy be measured or quantified?
You can calculate the amount of thermal energy in each sample by determining how much energy can be transferred from each one. One way to do this is to use the energy in the three samples to warm identical samples of cold water.
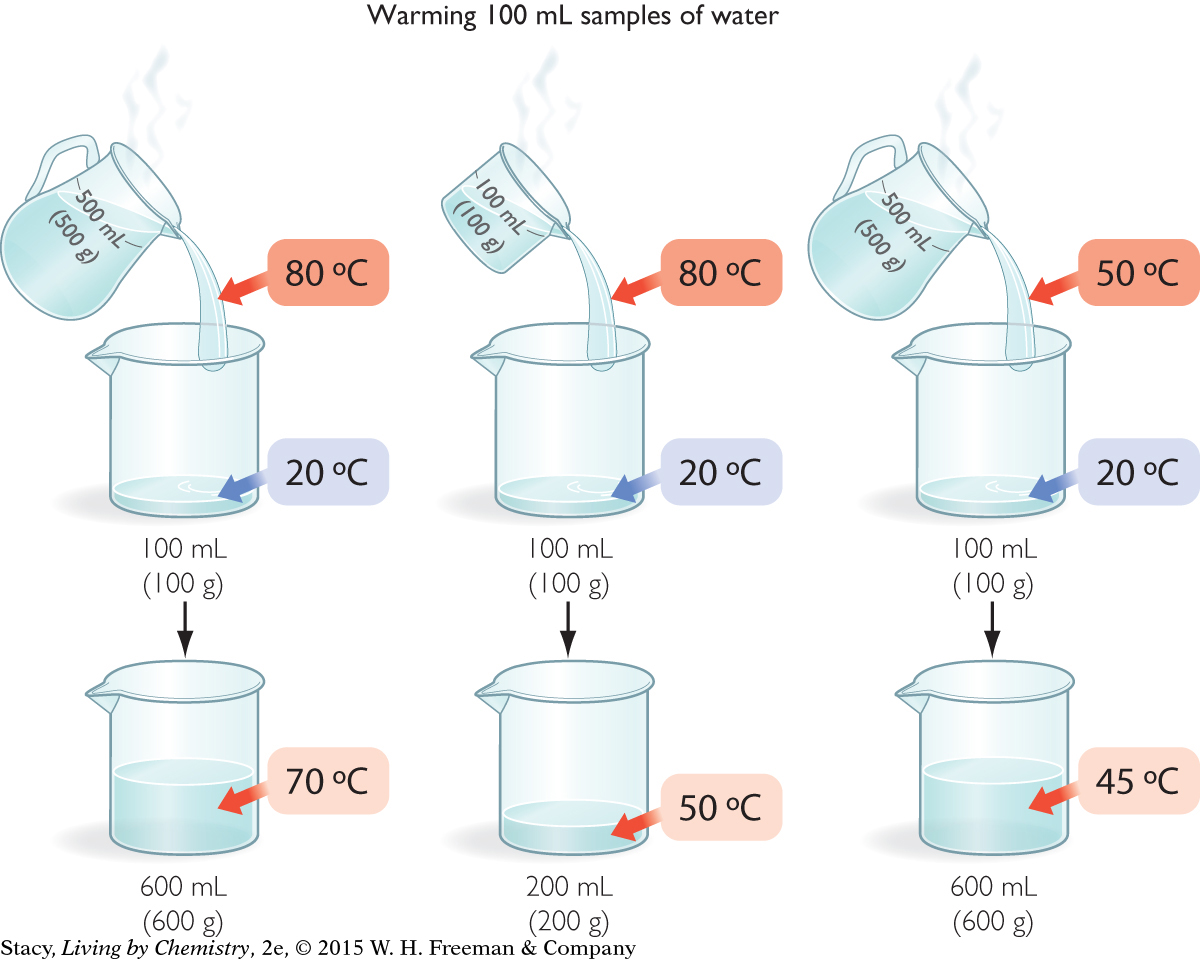
Notice that the large sample of water at 50 ºC warms the cold water sample nearly as much as the small sample of water at 80 ºC.
In each case, the mixture reaches thermal equilibrium. That is, the faster moving molecules in the hot sample slow down and the slower moving molecules in the cold sample speed up until they are all moving with the same average kinetic energy. The transfer of energy happens through collisions of the molecules as the samples mix. The temperature of the final mixture depends on the temperatures and the masses of the samples that were mixed.
A UNIT OF ENERGY: THE CALORIE
Scientists define a unit called a calorie to measure heat transfer. A calorie is the amount of energy needed to raise the temperature of 1 gram of water by 1 Celsius degree. So, this unit of energy is based on heat transfer to or from water. To determine the number of calories needed, you multiply the mass of the water by the temperature increase in Celsius degrees. This can be summarized by the mathematical equation for the heat transfer, q, in terms of the mass of water, m, and the temperature change, ΔT. The uppercase Greek letter delta, Δ, is used to represent a change in quantity.
q = m(1 cal/g · ºC)ΔT
(Remember, 1 g of water is equivalent to 1 mL of water at room temperature.)
So, for example, to raise the temperature of 500 grams of water by 10 ºC, from a temperature of 20 ºC to a temperature of 30 ºC, it would take 5000 calories of energy.
[For a review of this math topic, see MATH Spotlight: Averages on page A-7.]
Example 1
Calories
Suppose that you need to heat some water.
How many calories of energy does it take to heat a 75 mL sample of water for cocoa from 25 ºC to 38 ºC?
How many calories of energy does it take to heat a 2 L sample of water for a footbath from 25 ºC to 38 ºC?
Which sample of water contains more thermal energy: the water for cocoa or the water for the footbath?
Solution
Convert volume to mass in grams. Determine the change in temperature ΔT for both situations. Then use the equation for heat transfer to solve for q.
75 mL water = 75 g water
ΔT = 38 − 25 = 13ºC
q = m(1 cal/g · ºC)ΔT
= 75 g(1 cal/g · ºC)13ºC
= 975 calories
2 L water = 2000 g water
ΔT = 38 − 25 = 13ºC
q = m(1 cal/g · ºC)ΔT
= 2000 g(1 cal/g · ºC)13ºC
= 26,000 calories
The water in the footbath represents a greater amount of thermal energy.
Example 2
Conservation of Energy
You mix 300 mL of water at 60 ºC with 100 mL of water at 20 ºC.
Find the final temperature of the mixture.
Show that the heat transferred from the hot water is equal to the heat transferred to the cold water.
Solution
The final temperature will be a weighted average of the two initial temperatures. (Each temperature is “weighted” by multiplying it by the mass of each sample that is mixed.) The masses of the samples are 300 g and 100 g.
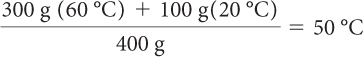
The final temperature is 50 ºC. It makes sense that the final temperature is closer to 60 ºC, since there was more of the 60 ºC water.
The calories of energy transferred is given by this equation:
q = m(1 cal/g · ºC)ΔT
Remember, 300 mL of water = 300 g of water.
Hot water: q = (300 g)(1 cal/g · °C)(50 °C − 60 °C) = − 3000 calories
Cold water: q = (100 g)(1 cal/g · °C)(50 °C − 20 °C) = 3000 calories
The negative sign means that energy is transferred from the hot water. The positive sign for the cold water indicates that energy is transferred to the cold water. Based on the calculated answers, energy is conserved.
LESSON SUMMARY
LESSON SUMMARY
What is the difference between temperature and heat?
KEY TERMS
thermal energy
calorie
Temperature and heat are different, although they are both related to the motion of atoms and molecules. The temperature of a substance is a measure of the average kinetic energy of its particles. Heat is a process of energy transfer to or from a sample of matter. Thermal energy is a term often used to describe the “energy content” of a sample. The thermal energy of a sample depends on the number of particles in a sample, whereas temperature is the same regardless of the size of the sample. A calorie is a unit of energy. It is defined as the energy required to raise the temperature of 1 g of water by 1 ºC. The energy transferred is referred to as heat.
Exercises
Reading Questions
If you heat up a large and a small sample of cold tap water to the same temperature, explain why it takes more energy to heat up the larger sample.
What is the difference between thermal energy and temperature?
Reason and Apply
How many calories of energy do you need to transfer for each of the following changes?
Raise the temperature of 1 g of water by 5 ºC.
Raise the temperature of 2 g of water by 5 ºC.
Raise the temperature of 9 g of water by 35 ºC.
Which will warm a child’s inflatable pool more: adding 500 g of water at 50 ºC or 100 g at 95 ºC? The temperature of the water in the pool is 20 ºC. Explain your reasoning.
Suppose that two water samples are mixed. Copy the data table and fill in the amounts of heat transferred.
How do the values in the last two columns compare?
How does the amount of heat transferred depend on the change in temperature?
How does the amount of heat transferred depend on the mass of each sample?

Suppose that you mix two water samples: 300 g of water at 20 ºC and 200 g of water at 50 ºC. What do you expect the final temperature of the water to be?
From a molecular viewpoint, explain how thermal equilibrium is reached when hot and cold water mix.