LESSON 121: How Balanced
THINK ABOUT IT
One reason that aqueous acidic solutions can be dangerous is because of the sensitivity of the human body to high concentrations of H+, or low pH. Because weak acids only dissociate to a small degree, the molarity of a weak acid solution alone does not provide information about the concentration of H+. So far, you have considered that the equilibrium constant K is a measure of the degree of dissociation. But is there a more specific relationship between K and the solution molarity?
How does K describe the concentrations in an equilibrium mixture?
To answer this question, you will explore
The Equilibrium-Constant Equation for a Weak Acid
The General Form of the Equilibrium-Constant Equation
The Equilibrium-Constant Equation for a Weak Acid
The Equilibrium-Constant Equation for a Weak Acid
INDUSTRY CONNECTION
INDUSTRY
CONNECTION
The main ingredients of soap are sodium hydroxide (pH 14) and vegetable oils. Soap is a salt of a fatty acid. To control the damaging effects of the high pH, soap makers test their soaps to make sure that they range from neutral (pH of 7) to somewhat basic (pH of 10). A soap with a pH above 10 is considered harsh. Soap with a pH less than 10 is suitable for use on skin, which is slightly acidic (pH 4 to 6). It is important that the pH of the soap is slightly basic as this helps to clean off the acid secretions on the skin, along with dirt, oil, and grease.

EXPLORING THE TOPIC
Many parts of the human body can only tolerate a specific range of pH values. For example, the normal pH range of your skin is 4 to 6, due to the presence of lactic acid from perspiration and of the acids that make up the outer skin layer. When you wash your hands with soaps with pH values that are much higher than that of your skin, this can cause skin irritation and harm beneficial microorganisms that reside in the skin. For this reason, small amounts of weak acids such as citric acid are added to hand soaps to adjust their pH.
Because weak acids do not dissociate completely, you might wonder how to determine the pH of a solution for a certain concentration of a weak acid. One way is to prepare solutions of various molarities and measure the pH. Another way is to calculate the pH by using the equilibrium constant K for a specific acid and the equilibrium-constant equation.
RELATIONSHIP BETWEEN K AND EQUILIBRIUM CONCENTRATIONS
In the previous lesson, K was introduced as a number that describes what is present in the equilibrium mixture. The equation below defines K more specifically for an acidic solution. The equation relates the equilibrium constant K, the concentrations of an acid, HA, and the ion products, H+ and A−, in an equilibrium mixture of an acid dissolved in water. The brackets, [ ], indicate the concentrations at equilibrium in moles per liter.
HA(aq) ⇋ H+(aq) + A−(aq)
For a weak acid solution, K is a very small number. There are very few ions in the solution because very few acid molecules dissociate. It is possible to determine the value of K for a specific weak acid by making a solution of known molarity and measuring the solution pH.
[H+] at equilibrium is equal to 10−pH. This relationship is determined by rearranging pH = −log[H+]. For the dissociation of a weak acid, [H+] is a tiny number.
[A−] = [H+] for a weak acid dissolved in water. For every H+ ion, there is one A− ion.
[HA] ≈ solution molarity. The equilibrium concentration of HA is approximately equal (“≈”) to the solution molarity because such a small amount dissociates.
Example 1
Determination of the Value of K
A student prepares a 0.10 M solution of acetic acid. The pH of the solution is 2.9. Determine the equilibrium constant K for lactic acid.
Solution
[H+] = 10–pH = 10−2.9 = 1.3 × 10−3 = 0.0013 M
[A−] = [H+] = 0.0013 M
[HA] ≈ [HA]total ≈ 0.10 M
Substituting the values in the equilibrium-constant equation gives:
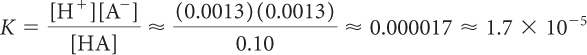
Note that all these calculations are approximate because they use the solution molarity to approximate the concentration of HA at equilibrium. Since very little HA dissociates, the equilibrium concentration of HA does not differ significantly from the solution molarity. In this case, the concentration of HA is ~75 times the concentration of H+.
USING K TO CALCULATE THE pH OF A WEAK ACID SOLUTION
Values of K for various weak acids are listed in the table. If you look up the value of K for a specific weak acid, you can use it to determine the solution pH. (The temperature is assumed to be 25° C.)
Important to Know
The concentration of H+ is so small that you might wonder why it matters at all. It turns out that the human body easily detects even small changes in [H+], for example, as a sour taste, a skin irritation, or as a stinging sensation in your eyes.

First, it is necessary to rearrange the equilibrium-constant equation to solve for [H+].
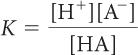
For an acid dissolved in water: [H+] = [A−]
Substituting for [A−] gives
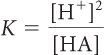
Solving for [H+] gives
[H+]2 = K[HA]
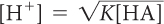
pH = −log[H+]
The next step is to find the value of K in a reference table and decide on a solution molarity.
Important to Know
The same value of K is used for different concentrations of the same acid at the same temperature.
Big Idea
Big Idea
The equilibrium constant K is useful in predicting the pH of a weak acidic solution.
Example 2
Determination of the pH of Artificial Lemon Juice
Citric acid is often added to juice to give it a sour taste. However, if the pH is below 3, many people will find that the juice is too sour to drink. Given that K = 7.2 × 10−4 = 0.00072 for the dissociation of citric acid, determine if the solutions listed below will have a pH that is below 3.
1.0 M
0.50 M
0.10 M
Solution

pH = −log[H+] ≈ −log(0.027) ≈ 1.6

pH = −log[H+] ≈ −log(0.019) ≈ 1.7

pH = −log[H+] ≈ −log(0.0084) ≈ 2.0
All three solutions have a pH less than 3, so they may all be too sour to drink.
The General Form of the Equilibrium-Constant Equation
The General Form of the Equilibrium-Constant Equation
So far, the discussion has centered on reversible processes involving dissociation of a substance into two pieces. However, the form of the equilibrium-constant equation changes depending on the balanced chemical equation for the reversible process. The table shows how the equilibrium-constant equation changes with different types of chemical processes. Examine the table to look for patterns.
HEALTH CONNECTION
HEALTH
CONNECTION
Is a super-sour taste a sign that your food has too much acid? Sour candy has always been popular, but daredevils now savor super-sour candies. Dentists say that foods with a pH below 4.0 have a bad effect on tooth enamel. Some super-sour candy, including super-sour gummy candies, have a pH between 2 and 3. A pH below 2 is approaching the level of sulfuric acid used in car batteries.

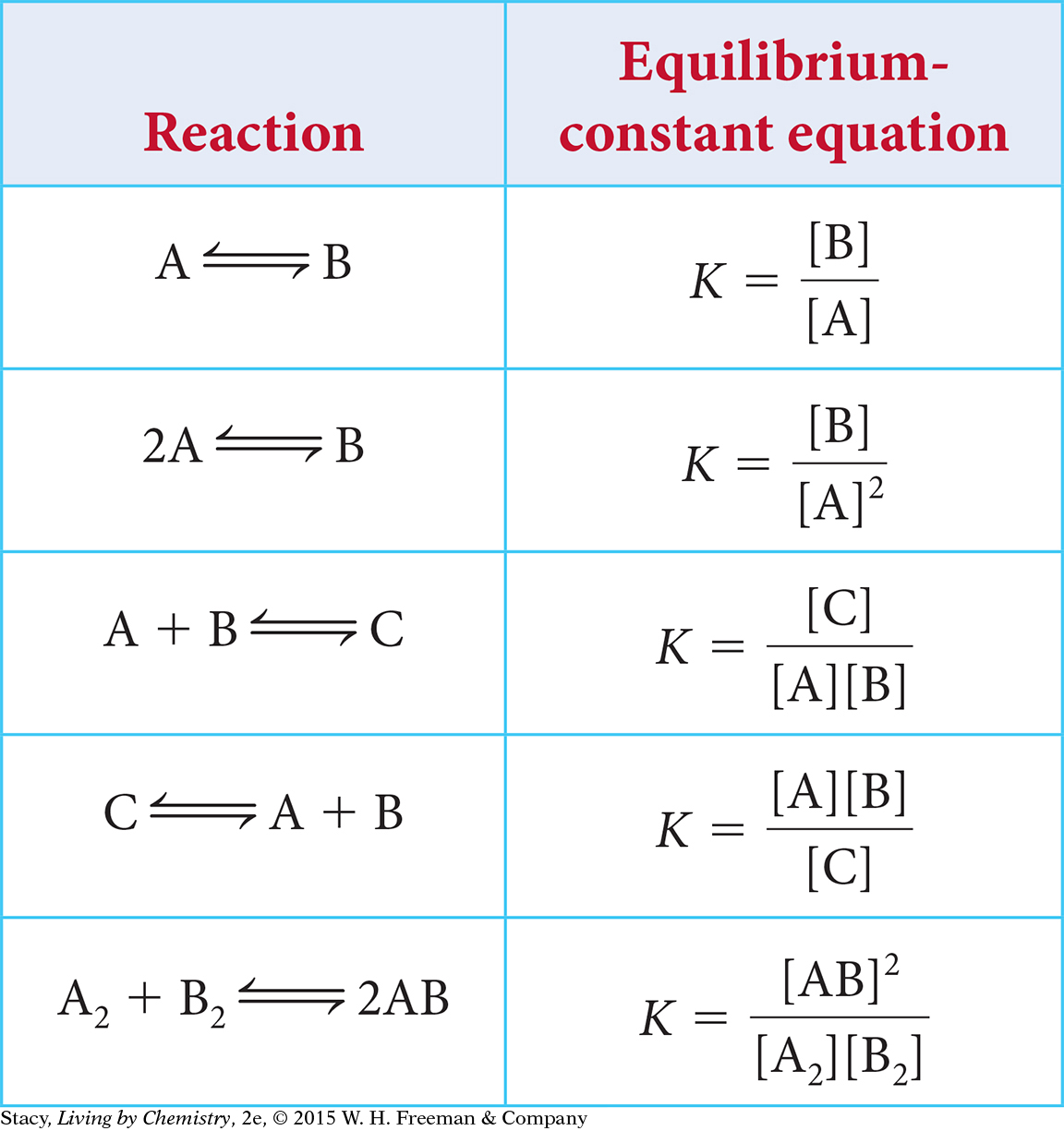
You might notice two important patterns.
The products are always in the numerator, and the starting substances are always in the denominator.
The coefficients in the chemical equation show up in the equilibrium-constant equation as exponents.
These patterns can be generalized as shown below.
aA + bB ⇋ cC + dD
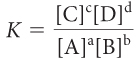
PURE SOLIDS AND LIQUIDS
The equilibrium-constant equation keeps track of concentrations that vary. This includes concentrations of substances in solution and concentrations of gases, which vary as gases expand and contract. However, pure solids and pure liquids do not appear in the equation. They are assigned a value of 1 because they don't have a “concentration” that changes.
Here are two examples.
| MgCO3(s) ⇋ MgO(s) + CO2(g) | K = [CO2] |
| PbCl2(s) ⇋ Pb2+(aq) + 2Cl−(aq) | K = [Pb2+][Cl−]2 |
LESSON SUMMARY
LESSON SUMMARY
How does K describe the concentrations in an equilibrium mixture?
KEY TERM
equilibrium-constant equation
A system at equilibrium reaches a balance between starting substances and products characterized by the equilibrium constant K. The concentrations adjust until the rates of the forward and reverse processes are equal. At equilibrium, there is a specific relationship between K and the concentrations of starting substances and products in an equilibrium mixture, called the equilibrium-constant equation. For a dissociation reaction, the relationship is:
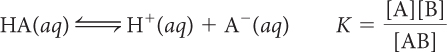
If K is known for a reversible process at a given temperature, it can be used in calculations for various equilibrium concentrations for this same system.
Exercises
Reading Questions
How can you use the equilibrium constant K to determine the pH of a weak acid solution?
Explain how to write the equilibrium-constant equation for a reversible process.
Reason and Apply
Use the information provided in the table to determine the equilibrium constant K for these weak acid solutions.
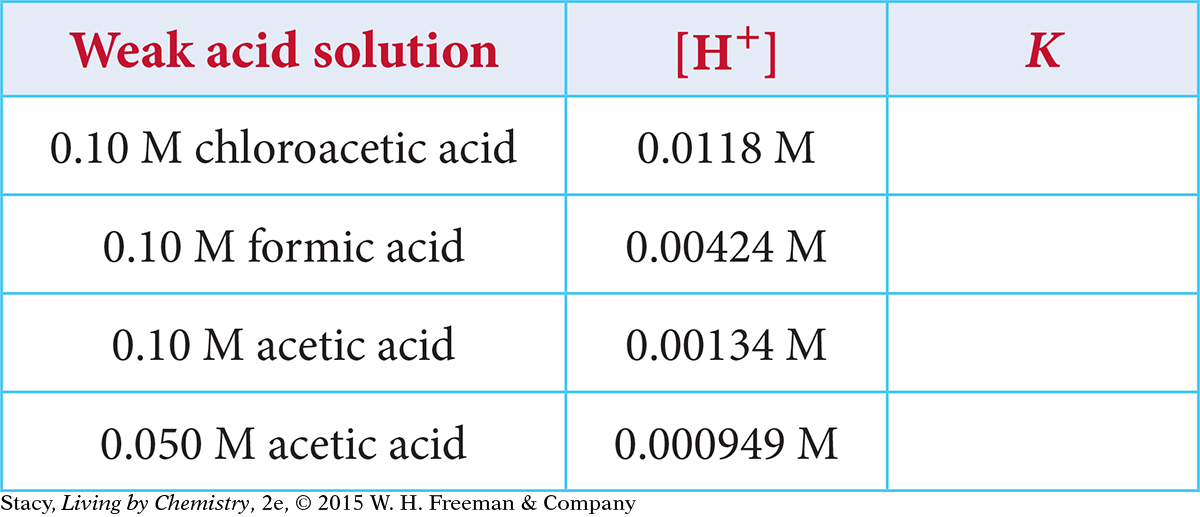 Page 636
Page 636Use the information provided in the table to determine the H+ concentration and the pH for these weak acid solutions.

Write equilibrium-constant equations for each reversible process.
NH3(aq) + H2O(l) ⇋ NH4+(aq) + OH2−(aq)
Na2SO4(s) ⇋ 2Na+(aq) + SO42−(aq)
C2H4(g) + H2(g) ⇋ C2H6(g)