Chapter 11: Transmembrane Transport of Ions and Small Molecules

Selective Movement of Ions Creates a Transmembrane Electric Gradient

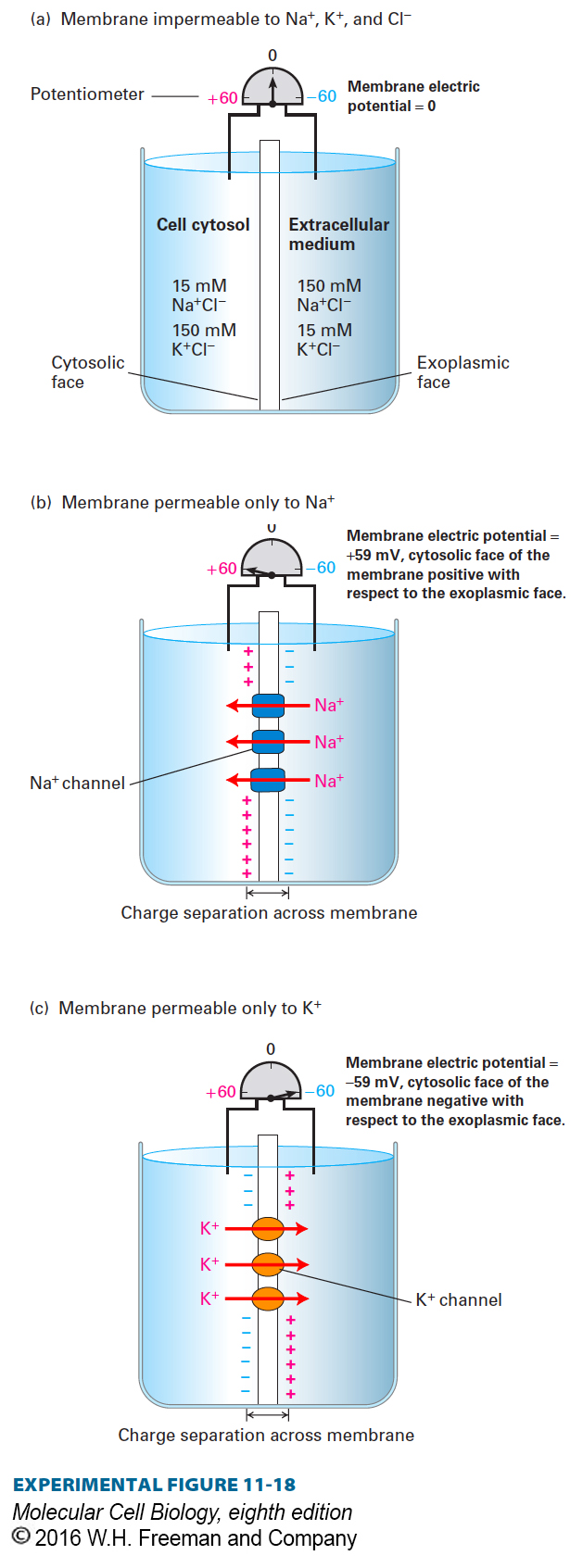
To help explain how an electric potential across the plasma membrane can arise, we first consider a set of simplified experimental systems in which a membrane separates a 150 mM NaCl/15 mM KCl solution (similar to the extracellular medium surrounding metazoan cells) on the right from a 15 mM NaCl/150 mM KCl solution (similar to that of the cytosol) on the left (Figure 11-18a). A potentiometer (voltmeter) is connected to both solutions to measure any electric potential across the membrane. Initially, both solutions contain an equal number of positive and negative ions. If the membrane is impermeable to all ions, no ions will flow across it. Furthermore, there will be no difference in voltage, or electric potential gradient, across the membrane, as shown in Figure 11-18a.

EXPERIMENTAL FIGURE 11-18 Generation of a transmembrane electric potential (voltage) depends on the selective movement of ions across a semipermeable membrane. In this experimental system, a membrane separates a 15 mM NaCl/150 mM KCl solution (left) from a 150 mM NaCl/15 mM KCl solution (right); these ion concentrations are similar to those in cytosol and blood, respectively. If the membrane separating the two solutions is impermeable to all ions (a), no ions can move across the membrane, and no electric potential is registered on the potentiometer connecting the two solutions. If the membrane is selectively permeable only to Na⁺ (b) or only to K⁺ (c), then diffusion of these ions through their respective channels leads to a separation of charge across the membrane. At equilibrium, the membrane potential caused by the charge separation becomes equal to the Nernst potential E_Na or E_K registered on the potentiometer. See the text for further explanation.

496

Now suppose that the membrane contains Na⁺ channels that accommodate Na⁺ ions but exclude K⁺ and Cl⁻ ions (Figure 11-18b). Na⁺ ions then tend to move down their concentration gradient from the right side to the left, leaving an excess of negative Cl⁻ ions compared with Na⁺ ions on the right side and generating an excess of positive Na⁺ ions compared with Cl⁻ ions on the left side. The excess Na⁺ on the left and Cl⁻ on the right remain near the respective surfaces of the membrane because the excess positive charges on one side of the membrane are attracted to the excess negative charges on the other side. The resulting separation of charge across the membrane constitutes an electric potential, or voltage, and the left (cytosolic) side of the membrane has excess positive charge with respect to the right.

As more and more Na⁺ ions move through channels across the membrane, the magnitude of this charge difference (i.e., voltage) increases. However, continued right-to-left movement of the Na⁺ ions is eventually inhibited by the mutual repulsion between the excess positive (Na⁺) charges accumulated on the left side of the membrane and by the attraction of Na⁺ ions to the excess negative charges built up on the right side. The system soon reaches an equilibrium point at which the two opposing factors that determine the movement of Na⁺ ions—the membrane electric potential and the ion concentration gradient—balance each other out. At equilibrium, there is no net movement of Na⁺ ions across the membrane. Thus this membrane, like all cellular membranes, acts as a capacitor—a device consisting of a thin sheet of nonconducting material (the hydrophobic interior) surrounded on both sides by electrically conducting material (the polar phospholipid head groups and the ions in the surrounding aqueous solution) that can store positive charges on one side and negative charges on the other.

If a membrane is permeable only to Na⁺ ions, then at equilibrium, the measured electric potential across the membrane equals the sodium equilibrium potential in volts, E_Na. The magnitude of E_Na is given by the Nernst equation, which is derived from basic principles of physical chemistry:

497

where R (the gas constant) = 1.987 cal/(degree · mol), or 8.28 joules/(degree · mol); T (the absolute temperature in degrees Kelvin) = 293 °K at 20 °C; Z (the charge, also called the valence) is here equal to +1; F (the Faraday constant) = 23,062 cal/(mol · V), or 96,000 coulombs/(mol · V); and [Na_left] and [Na_right] are the Na⁺ concentrations on the left and right sides, respectively, at equilibrium. By convention, the potential is expressed as the cytosolic face of the membrane relative to the exoplasmic face, and the equation is written with the ion concentration of the extracellular solution (here the right side of the membrane) placed in the numerator and that of the cytosol in the denominator.

At 20 °C (room temperature), Equation 11-2 reduces to

If [Na_right]/[Na_left] = 10, a tenfold ratio of concentrations as in Figure 11-18b, then E_Na = +0.059 V (or +59 mV), with the left, cytosolic side positive with respect to the right, exoplasmic side.

If the membrane is permeable only to K⁺ ions and not to Na⁺ or Cl⁻ ions, then a similar equation describes the potassium equilibrium potential E_K:

The magnitude of the membrane electric potential is the same (59 mV, for a tenfold difference in ion concentrations), but the left, cytosolic side is now negative with respect to the right, exoplasmic (Figure 11-18c), so the polarity is opposite to that obtained across a membrane selectively permeable to Na⁺ ions.