An economy’s output of goods and services—its GDP—depends on (1) its quantity of inputs, called the factors of production, and (2) its ability to turn inputs into output, as represented by the production function.

Factors of production are the inputs used to produce goods and services. The two most important factors of production are capital and labor. Capital is the set of tools that workers use: the construction worker’s crane, the accountant’s calculator, and this author’s personal computer. Labor is the time people spend working. We use the symbol K to denote the amount of capital and the symbol L to denote the amount of labor.

In this chapter we take the economy’s factors of production as given. In other words, we assume that the economy has a fixed amount of capital and a fixed amount of labor. We write

The overbar means that each variable is fixed at some level. In Chapter 8 we examine what happens when the factors of production change over time, as they do in the real world. For now, to keep our analysis simple, we assume fixed amounts of capital and labor.

We also assume here that the factors of production are fully utilized. That is, no resources are wasted. Again, in the real world, part of the labor force is unemployed, and some capital lies idle. In Chapter 7 we examine the reasons for unemployment, but for now we assume that capital and labor are fully employed.

50

The available production technology determines how much output is produced from given amounts of capital and labor. Economists express this relationship using a production function. Letting Y denote the amount of output, we write the production function as

Y = F(K, L).

This equation states that output is a function of the amount of capital and the amount of labor.

The production function reflects the available technology for turning capital and labor into output. If someone invents a better way to produce a good, the result is more output from the same amounts of capital and labor. Thus, technological change alters the production function.

Many production functions have a property called constant returns to scale. A production function has constant returns to scale if an increase of an equal percentage in all factors of production causes an increase in output of the same percentage. If the production function has constant returns to scale, then we get 10 percent more output when we increase both capital and labor by 10 percent. Mathematically, a production function has constant returns to scale if

zY = F(zK, zL)

for any positive number z. This equation says that if we multiply both the amount of capital and the amount of labor by some number z, output is also multiplied by z. In the next section we see that the assumption of constant returns to scale has an important implication for how the income from production is distributed.

As an example of a production function, consider production at a bakery. The kitchen and its equipment are the bakery’s capital, the workers hired to make the bread are its labor, and the loaves of bread are its output. The bakery’s production function shows that the number of loaves produced depends on the amount of equipment and the number of workers. If the production function has constant returns to scale, then doubling the amount of equipment and the number of workers doubles the amount of bread produced.

We can now see that the factors of production and the production function together determine the quantity of goods and services supplied, which in turn equals the economy’s output. To express this mathematically, we write

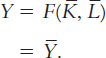
In this chapter, because we assume that the supplies of capital and labor and the technology are fixed, output is also fixed (at a level denoted here as ). When we discuss economic growth in Chapter 8 and Chapter 9, we will examine how increases in capital and labor and advances in technology lead to growth in the economy’s output.

51