In this chapter we showed that if the quantity of real money balances demanded depends on the cost of holding money, the price level depends on both the current money supply and the future money supply. This appendix develops the Cagan model to show more explicitly how this relationship works.11

To keep the math as simple as possible, we posit a money demand function that is linear in the natural logarithms of all the variables. The money demand function is

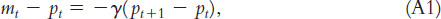
where m_t is the log of the quantity of money at time t, p_t is the log of the price level at time t, and γ is a parameter that governs the sensitivity of money demand to the rate of inflation. By the property of logarithms, m_t − p_t is the log of real money balances, and p_t+1 − p_t is the inflation rate between period t and period t + 1. This equation states that if inflation goes up by 1 percentage point, real money balances fall by γ percent.

We have made a number of assumptions in writing the money demand function in this way. First, by excluding the level of output as a determinant of money demand, we are implicitly assuming that it is constant. Second, by including the rate of inflation rather than the nominal interest rate, we are assuming that the real interest rate is constant. Third, by including actual inflation rather than expected inflation, we are assuming perfect foresight. All of these assumptions are made to keep the analysis as simple as possible.

We want to solve Equation A1 to express the price level as a function of current and future money. To do this, note that Equation A1 can be rewritten as

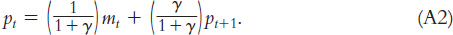
This equation states that the current price level p_t is a weighted average of the current money supply m_t and the next period’s price level p_t+1. The next period’s price level will be determined the same way as this period’s price level:

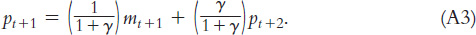
136

Now substitute Equation A3 for p_t+1 in Equation A2 to obtain

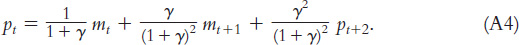
Equation A4 states that the current price level is a weighted average of the current money supply, the next period’s money supply, and the following period’s price level. Once again, the price level in period t + 2 is determined as in Equation A2:

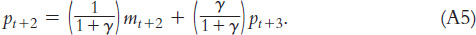
Now substitute Equation A5 into Equation A4 to obtain

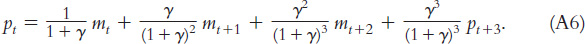
By now you see the pattern. We can continue to use Equation A2 to substitute for the future price level. If we do this an infinite number of times, we find

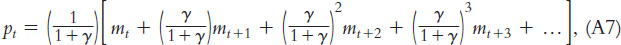
where “…” indicates an infinite number of analogous terms. According to Equation A7, the current price level is a weighted average of the current money supply and all future money supplies.

Note the importance of γ, the parameter governing the sensitivity of real money balances to inflation. The weights on the future money supplies decline geometrically at rate γ/(1 + γ). If γ is small, then γ/(1 + γ) is small, and the weights decline quickly. In this case, the current money supply is the primary determinant of the price level. (Indeed, if γ equals zero, we obtain the quantity theory of money: the price level is proportional to the current money supply, and the future money supplies do not matter at all.) If γ is large, then γ/(1 + γ) is close to 1, and the weights decline slowly. In this case, the future money supplies play a key role in determining today’s price level.

Finally, let’s relax the assumption of perfect foresight. If the future is not known with certainty, then we should write the money demand function as

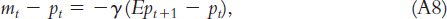
where Ep_t+1 is the expected price level. Equation A8 states that real money balances depend on expected inflation. By following steps similar to those above, we can show that

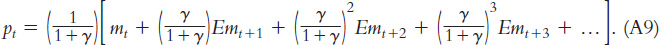
Equation A9 states that the price level depends on the current money supply and expected future money supplies.

Some economists use this model to argue that credibility is important for ending hyperinflation. Because the price level depends on both current and expected future money, inflation depends on both current and expected future money growth. Therefore, to end high inflation, both money growth and expected money growth must fall. Expectations, in turn, depend on credibility—the perception that the central bank is committed to a new, more stable policy.

137

How can a central bank achieve credibility in the midst of hyperinflation? Credibility is often achieved by removing the underlying cause of the hyperinflation—the need for seigniorage. Thus, a credible fiscal reform is often necessary for a credible change in monetary policy. This fiscal reform might take the form of reducing government spending and making the central bank more independent from the government. Reduced spending decreases the need for seigniorage, while increased independence allows the central bank to resist government demands for seigniorage.