PROBLEMS AND APPLICATIONS
An economy described by the Solow growth model has the following production function:
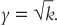
Solve for the steady-state value of y as a function of s, n, g, and d.
A developed country has a saving rate of 28 percent and a population growth rate of 1 percent per year. A less-developed country has a saving rate of 10 percent and a population growth rate of 4 percent per year. In both countries, g = 0.02 and δ = 0.04. Find the steady-state value of y for each country.
What policies might the less-developed country pursue to raise its level of income?
In the United States, the capital share of GDP is about 30 percent; the average growth in output is about 3 percent per year; the depreciation rate is about 4 percent per year; and the capital–output ratio is about 2.5. Suppose that the production function is Cobb–Douglas, so that the capital share in output is constant, and that the United States has been in a steady state. (For a discussion of the Cobb–Douglas production function, see the appendix to Chapter 3.)
What must the saving rate be in the initial steady state? [Hint: Use the steady-state relationship, sy = (δ + n + g)k.]
What is the marginal product of capital in the initial steady state?
Suppose that public policy raises the saving rate so that the economy reaches the Golden Rule level of capital. What will the marginal product of capital be at the Golden Rule steady state? Compare the marginal product at the Golden Rule steady state to the marginal product in the initial steady state. Explain.
What will the capital–output ratio be at the Golden Rule steady state? (Hint: For the Cobb–Douglas production function, the capital–output ratio is related to the marginal product of capital.)
What must the saving rate be to reach the Golden Rule steady state?
Page 279Prove each of the following statements about the steady state with population growth and technological progress.
The capital–output ratio is constant.
Capital and labour each earn a constant share of an economy’s income. [Hint: Recall the definition MPK = f(k + 1) – f(k).]
Total capital income and total labour income both grow at the rate of population growth plus the rate of technological progress, n + g.
The real rental price of capital is constant, and the real wage grows at the rate of technological progress g. (Hint: The real rental price of capital equals total capital income divided by the capital stock, and the real wage equals total labour income divided by the labour force.)
Two countries, Richland and Poorland, are described by the Solow growth model. They have the same Cobb–Douglas production function, F(K,αL) = A KαL1–α, but with different quantities of capital and labour. Richland saves 32 percent of its income, while Poorland saves 10 percent. Richland has population growth of 1 percent per year, while Poorland has population growth of 3 percent. (The numbers in this problem are chosen to be approximately realistic descriptions of rich and poor nations.) Both nations have technological progress at a rate of 2 percent per year and depreciation at a rate of 5 percent per year.
What is the per worker production function f(k)?
Solve for the ratio of Richland’s steady-state income per worker to Poorland’s. (Hint: The parameter α will play a role in your answer.)
If the Cobb–Douglas parameter α takes the conventional value of about one-third, how much higher should income per worker be in Richland compared to Poorland?
Income per worker in Richland is actually 16 times income per worker in Poorland. Can you explain this fact by changing the value of the parameter α? What must it be? Can you think of any way of justifying such a value for this parameter? How else might you explain the large difference in income between Richland and Poorland?
The amount of education the typical person receives varies substantially among countries. Suppose you were to compare a country with a highly educated labour force and a country with a less educated labour force. Assume that education affects only the level of the efficiency of labour. Also assume that the countries are otherwise the same: they have the same saving rate, the same depreciation rate, the same population growth rate, and the same rate of technological progress. Both countries are described by the Solow model and are in their steady states. What would you predict for the following variables?
The rate of growth of total income.
The level of income per worker.
The real rental price of capital.
The real wage.
This question asks you to analyze in more detail the two-sector endogenous growth model presented in the text.
Rewrite the production function for manufactured goods in terms of output per effective worker and capital per effective worker.
In this economy, what is break-even investment (the amount of investment needed to keep capital per effective worker constant)?
Write down the equation of motion for k, which shows Δk as saving minus break-even investment. Use this equation to draw a graph showing the determination of steady-state k. (Hint: This graph will look much like those we used to analyze the Solow model.)
In this economy, what is the steady-state growth rate of output per worker Y/L? How do the saving rate s and the fraction of the labour force in universities u affect this steady-state growth rate?
Using your graph, show the impact of an increase in u. (Hint: This change affects both curves.) Describe both the immediate and the steady-state effects.
Based on your analysis, is an increase in u an unambiguously good thing for the economy? Explain.