MORE PROBLEMS AND APPLICATIONS
In the economy of Solovia, the owners of capital get two-thirds of national income, and the workers receive one-third.
The men of Solovia stay at home performing household chores, while the women work in factories. If some of the men started working outside the home so that the labour force increased by 5 percent, what would happen to the measured output of the economy? Does labour productivity—defined as output per worker—increase, decrease, or stay the same? Does total factor productivity increase, decrease, or stay the same?
In year 1, the capital stock was 6, the labour input was 3, and output was 12. In year 2, the capital stock was 7, the labour input was 4, and output was 14. What happened to total factor productivity between the two years?
Labour productivity is defined as Y/L, the amount of output divided by the amount of labour input. Start with the growth-accounting equation and show that the growth in labour productivity depends on growth in total factor productivity and growth in the capital–labour ratio. In particular, show that
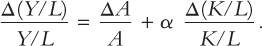
(Hint: You may find the following mathematical trick helpful. If z = wx, then the growth rate of z is approximately the growth rate of w plus the growth rate of x. That is,
Δz/z ≈ Δw/w + Δx/x.)
Suppose an economy described by the Solow model is in a steady state with population growth n of 1.8 percent per year and technological progress g of 1.8 percent per year. Total output and total capital grow at 3.6 percent per year. Suppose further that the capital share of output is 1/3. If you used the growth-accounting equation to divide output growth into three sources—capital, labour, and total factor productivity—how much would you attribute to each source?