20.1 CHOOSING THE APPROPRIATE STATISTICAL TEST

CHOOSING THE APPROPRIATE STATISTICAL TEST
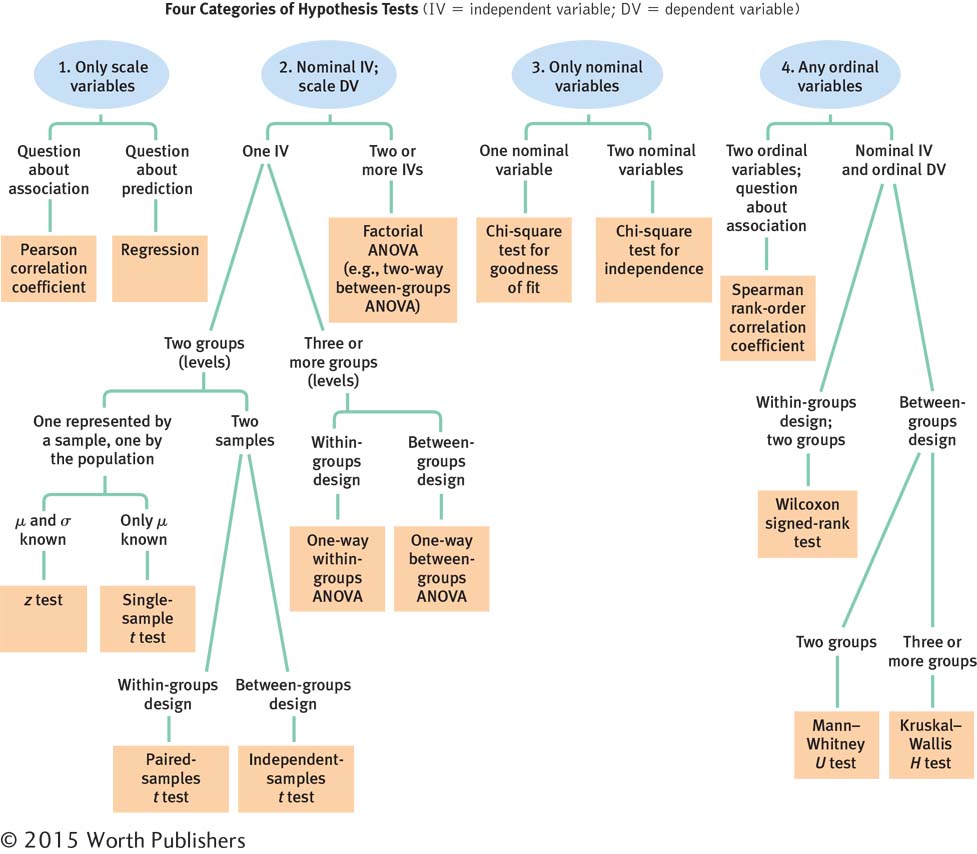
We have learned four categories of statistical tests:
Statistical tests in which all variables are scale
Statistical tests in which the independent variable (or variables) is nominal, but the dependent variable is scale
Statistical tests in which all variables are nominal
Statistical tests in which any variable is ordinal
Category 1: Two Scale Variables
If we have a research design with only scale variables, we have two choices about how to analyze the data. The only question we have to answer is: Does the research question pertain to an association (or relation) between two variables or does it pertain to the degree to which one variable predicts the other? If the research question is about association, then we choose the Pearson correlation coefficient. If it is about prediction, then we choose regression. The decisions for category 1 are represented in Table E-1. (Note that the relation must be linear.)

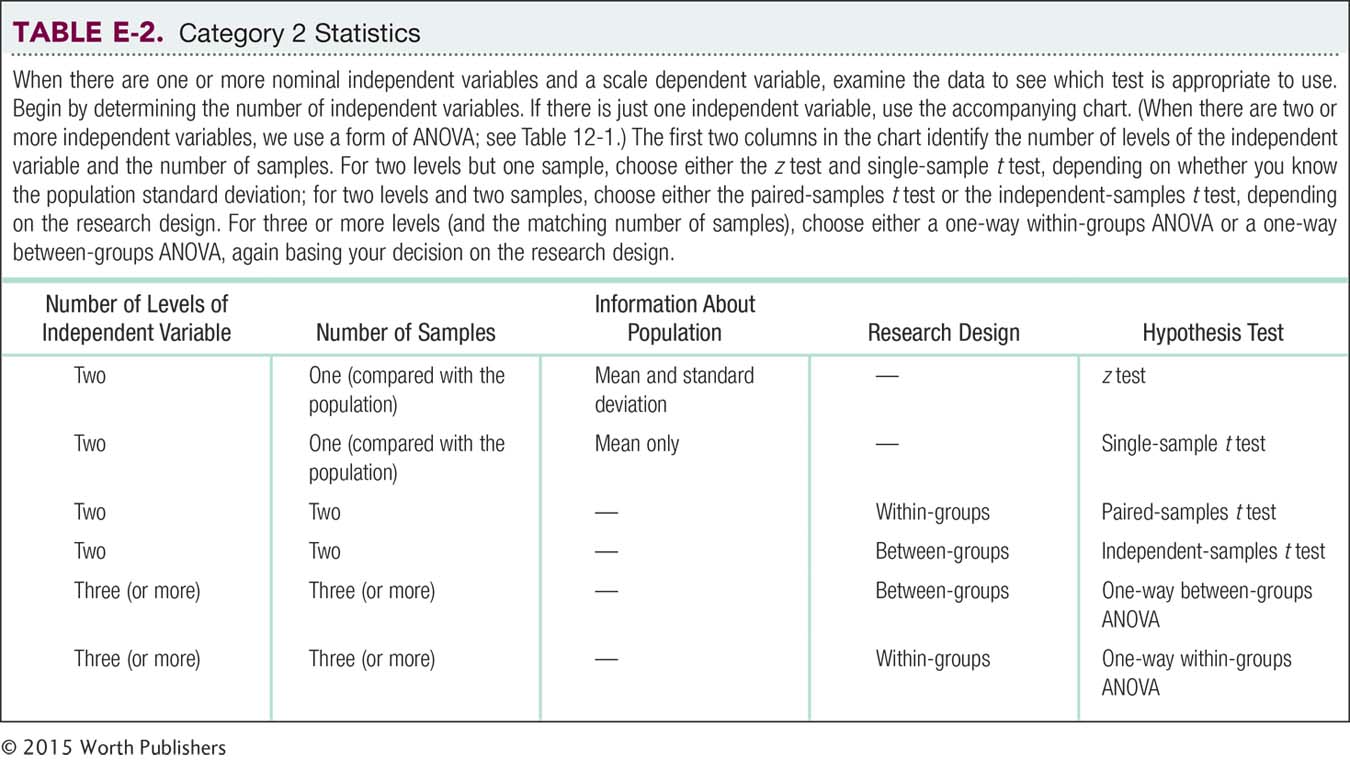
Category 2: Nominal Independent Variable(s) and a Scale Dependent Variable
If the research design includes one or more nominal independent variables and a scale dependent variable, then we have several choices. The next question pertains to the number of independent variables.
If there is just one independent variable, then we ask ourselves how many levels it has.
If there are two levels, but just one sample—that is, one level is represented by the sample and one level by the population—
then we use either a z test or a single- sample t test. It is unusual to know enough about a population that we only need to collect data from a single sample. If this is the case, however, and we know both the population mean and the population standard deviation, then we can use a z test. If this is the case and we know only the population mean (but not the population standard deviation), then we use the single- sample t test. If there are two levels, each represented by a sample (either a single sample in which everyone participates in both levels or two different samples, one for each level), then we use either a paired-
samples t test (if all participants are in both levels of the independent variable) or an independent- samples t test (if participants are in only one level of the independent variable). If there are three or more levels, then we use a form of a one-
way ANOVA. We examine the research design to determine whether it is a between- groups ANOVA (participants are in just one level of the independent variable) or a within- groups ANOVA (participants are in all levels of the independent variable).
If there are at least two independent variables, we must use a form of ANOVA. Remember, we name ANOVAs according to the number of independent variables (one-
way, two- way, three- way) and the research design (between- groups, within- groups).
The decisions about data that fall into category 2 and have one independent variable are summarized in Table E-2. For those with two or more independent variables, see Table 12-1.
Category 3: One or Two Nominal Variables
If we have a design with only nominal variables—

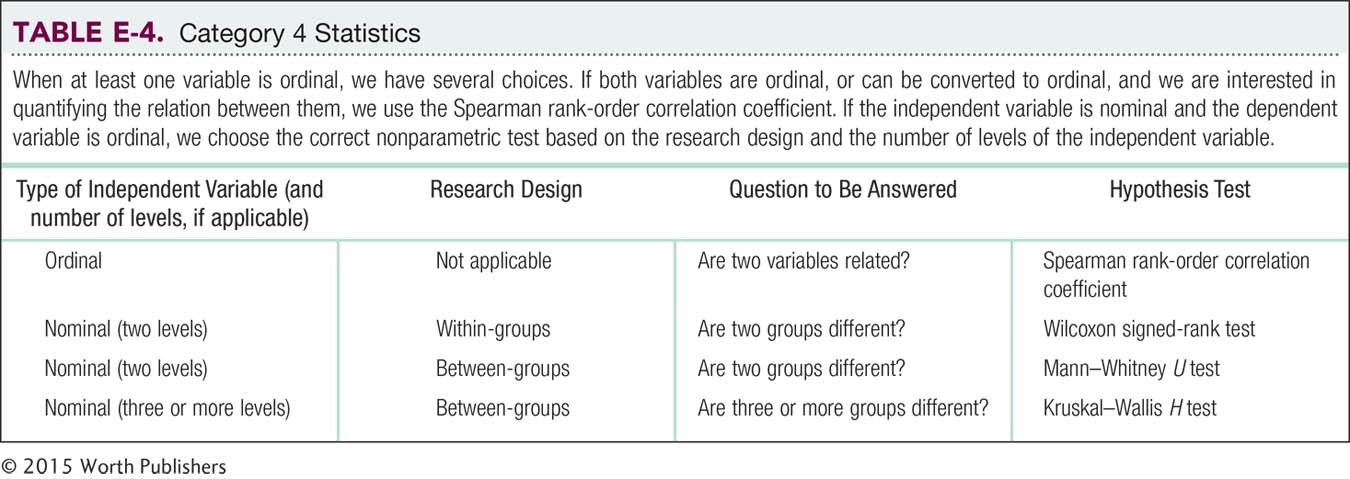
Category 4: At Least One Ordinal Variable
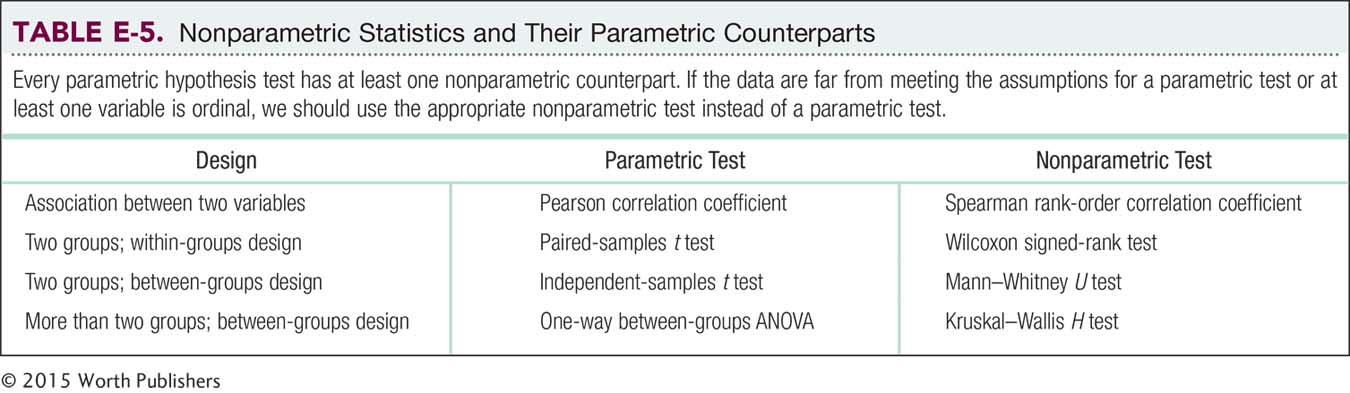
If we have a design with even one ordinal variable or a design in which it makes sense to convert the data from scale to ordinal, then we have several choices, as seen in Table E-4. All these choices have parallel parametric hypothesis tests, as seen in Table E-5. For situations in which we want to investigate the relation between two ordinal variables, we use the Spearman rank-
The decisions we’ve outlined are summarized in Figure E-
By asking the right questions about our variables and research design, we can choose the appropriate hypothesis test for our research.