REPORTING STATISTICS

F-1

In Chapter 10, How It Works 10.1, we described a study about gender differences in humor (Azim, Mobbs, Jo, Menon, & Reiss, 2005). Let’s recap the results of the analyses and then use this information to report statistics in the Methods and Results sections of a paper written in the style of the American Psychological Association (APA). In the analyses of the humor data, we used fictional data that had the same means as the actual study by Azim and colleagues. We used the following raw data:

Percentage of cartoons labeled as “funny”

Women: 84, 97, 58, 90

Men: 88, 90, 52, 97, 86

We conducted an independent-samples t test on these data and found a test statistic, t, of −0.03. This test statistic was not beyond the cutoff, so we failed to reject the null hypothesis. We cannot conclude that men and women, on average, find different percentages of the cartoons to be funny; we can only conclude that this study did not provide evidence that women and men are different on this variable.

The statistics for this test, as reported in a journal article, would include the symbol for the statistic, the degrees of freedom, the value of the test statistic, and, for statistics calculated by hand, whether the p value associated with the test statistic was less than or greater than the cutoff p level of 0.05. In the humor example, the statistics would read:

t(7) = −0.03, p > 0.05

(Note that when we conducted this hypothesis test using SPSS, we got an exact p value of 0.977, so we would say p = 0.98 instead of p > 0.05 if we had used software.) In addition to the statistics, we also would report the means and standard deviations for the two samples:

Women: M = 82.25, SD = 17.02; Men: M = 82.60, SD = 18.13

We can also calculate that the percentage difference between women and men is 82.25 − 82.60 = −0.35. There is just a 0.35% difference between women and men.

In How It Works 10.3, we calculated a confidence interval for these data. The 95% confidence interval, centered around the difference between means of 82.25 − 82.60 = −0.35, is [−27.88, 27.18].

In How It Works 10.4, we calculated the effect size for this study, a Cohen’s d of −0.02. We now have sufficient information to write up these findings.

There are three topics to consider when reporting statistics, all covered in various sections of the Publication Manual of the American Psychological Association (APA, 2010):

To justify the study, we first report the results of the statistical power analyses that were conducted before the data were collected. Then we report any information related to the reliability and validity of the measured variables. This information usually goes in the Methods section of the paper.

To summarize this aspect of the findings, we include in the Methods section:

The Results section should include any relevant summary statistics. For analyses with a scale dependent variable, include means, standard deviations, and sample sizes for each cell in the research design. For analyses with a nominal dependent variable (chi-square analyses), include the frequencies (counts) for each cell; there won’t be means or standard deviations because there are no scores on a scale measure.

Summary statistics are sometimes presented first in a Results section but are more typically presented after a description of each hypothesis test. If there are only two or three cells, then the summary statistics are typically presented in the text; if there are more cells, then these statistics should be displayed in a table or figure.

Reports of hypothesis tests typically begin by reiterating the hypothesis to be tested and then describing the test that was conducted, including the independent and dependent variables. The results of the hypothesis test are then presented, usually including the symbol for the statistic, the degrees of freedom, the actual value of the statistic, and, if using software, the actual p value associated with that statistic. The format for reporting this information is included after each hypothesis test in this text and is presented again in Table F-1.

F-2

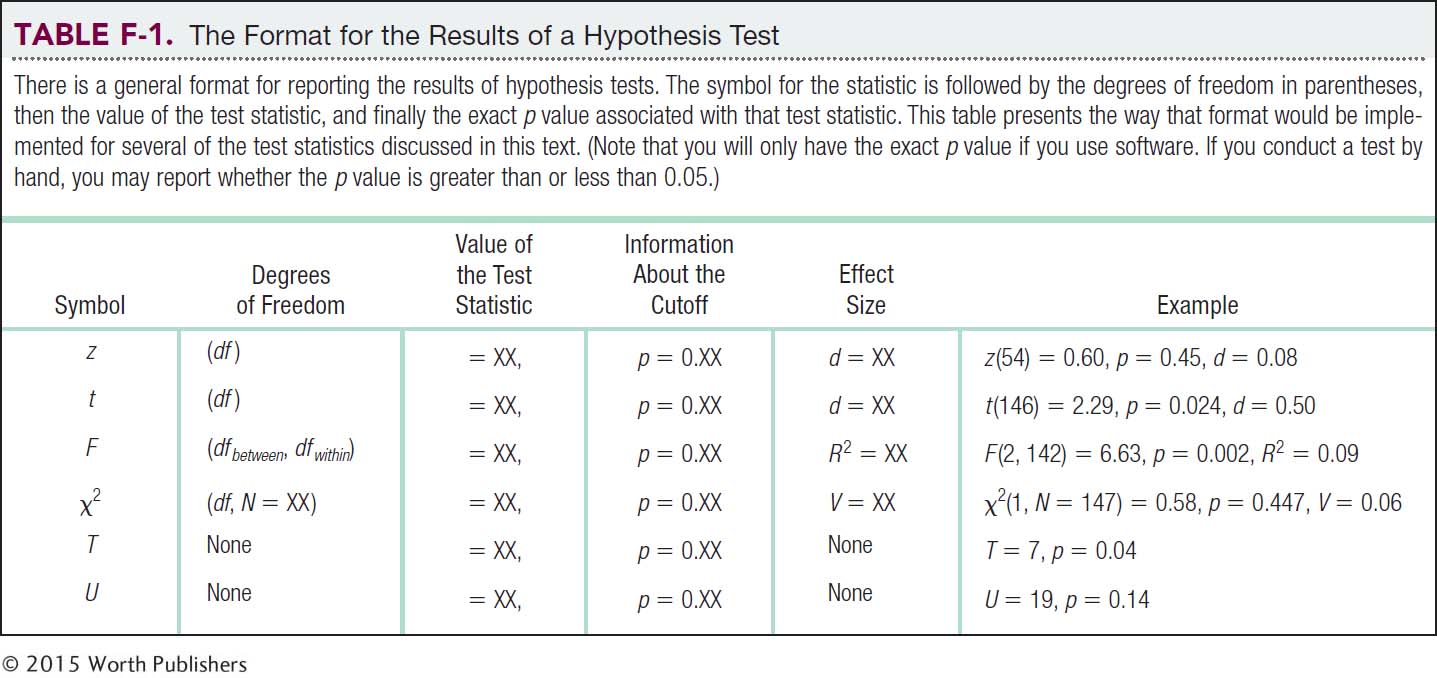
After the statistics are presented, a brief statement summarizes the results, indicating the direction of any effects. This brief statement does not draw conclusions beyond the actual finding. In the Results section, researchers do not discuss the finding in terms of the general theories in the field or in terms of its potential implications or applications (which go, appropriately enough, in the Discussion section). Researchers should present the results of all hypothesis tests that they conducted, even those in which they failed to reject the null hypothesis.

To summarize this aspect of Results sections:

The statistics for the study from How It Works in Chapter 10 that compared the mean percentages of cartoons that women and men found funny might be reported as follows:

F-3

To examine the hypothesis that women and men, on average, find different percentages of cartoons funny, we conducted an independent-samples t test. The independent variable was gender, with two levels: female and male. The dependent variable was the percentage of cartoons deemed funny. There was not a statistically significant effect of gender, t(7) = −0.03, p = 0.98; this study does not provide evidence that women (M = 82.25, SD = 17.02) and men (M = 82.60, SD = 18.13) deem, on average, different percentages of cartoons to be funny. The difference between the mean percentages for women and men is just 0.35%.

It is no longer enough to simply present the descriptive statistics and the results of the hypothesis test. As of the 2010 edition of its Publication Manual, the APA requires that effect sizes and confidence intervals be included when relevant. The effect-size estimate is often included as part of the report of the statistics, just after the p value. There is often a statement that indicates the size of the effect in words, not just in numbers. The confidence interval can be presented after the effect size, abbreviated as “95% CI” with the actual interval in brackets. Note that nonparametric tests often do not have associated measures of effect size or confidence intervals. In these cases, researchers should provide enough descriptive information for readers to interpret the findings.

To summarize this aspect of the Results sections, we include:

For the study on humor, we might report the effect size as part of the traditional statistics that we described above: There was not a statistically significant effect of gender, t(7) = −0.03, p = 0.98, d = −0.02, 95% CI [−28.37, 27.67]; this was a small, almost nonexistent, effect. In fact, there is only a 0.35% difference between the mean percentages for women and men. This study does not provide evidence that men and women, on average, rate different percentages of cartoons as funny.

F-4

For the humor study, we can now pull the parts together. Here is how the results would be reported:

To examine the hypothesis that women and men, on average, find different percentages of cartoons funny, we conducted an independent-samples t test. The independent variable was gender, with two levels: female and male. The dependent variable was the percentage of cartoons deemed funny. There was not a statistically significant effect of gender, t(7) = −0.03, p = 0.98, d = −0.02, 95% CI [−28.37, 27.67]; this was a small, almost nonexistent, effect.

Based on the hypothesis test and the confidence interval, this study does not provide evidence that women (M = 82.25, SD = 17.02) and men (M = 82.60, SD = 18.13) deem, on average, different percentages of cartoons to be funny. In fact, there is only a very small difference between the mean percentages for women and men, just 0.35%.