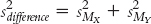nolanessentials3e

Exercises

Clarifying the Concepts

Question 10.1

10.1	When is it appropriate to use the independent-samples t test?

Question 10.2

10.2	Explain random assignment and what it controls.

Question 10.3

10.3	What are independent events?

Question 10.4

10.4	Explain how the paired-samples t test helps us evaluate individual differences and the independent-samples t test helps us evaluate group differences.

Question 10.5

10.5	As they relate to comparison distributions, what is the difference between mean differences and differences between means?

Question 10.6

10.6	As measures of variability, what is the difference between standard deviation and variance?

Question 10.7

10.7	What is the difference between s²_X and s²_Y?

Question 10.8

10.8	What is pooled variance?

Question 10.9

10.9	Why would we want the variability estimate based on a larger sample to count more (to be more heavily weighted) than one based on a smaller sample?

Question 10.10

10.10

Define the symbols in the following formula:

Question 10.11

10.11

How do confidence intervals relate to margin of error?

Question 10.12

10.12

What is the difference between pooled variance and pooled standard deviation?

Question 10.13

10.13

How does the size of the confidence interval relate to the precision of the prediction?

Question 10.14

10.14

Why does the effect-size calculation use standard deviation rather than standard error?

Question 10.15

10.15

Explain how we determine standard deviation (needed to calculate Cohen’s d) from the several steps of calculations we made to determine standard error.

Question 10.16

10.16

For an independent-samples t test, what is the difference between the formula for the t statistic and the formula for Cohen’s d?

Question 10.17

10.17

How do we interpret effect size using Cohen’s d?

Calculating the Statistic

Question 10.18

10.18

In the next column are several sample means. For each class, calculate the differences between the means for students who sit in the front versus the back of a classroom.

Mean Test Grades	Students in the Front	Students in the Back
Class 1	82	78
Class 2	79.5	77.41
Class 3	71.5	76
Class 4	72	71.3

Question 10.19

10.19

Consider the following data from two independent groups:

Group 1: 97, 83, 105, 102, 92

Group 2: 111, 103, 96, 106

Calculate s² for group 1 and for group 2.
Calculate df_X, df_Y, and df_total.
Determine the critical values for t, assuming a two-tailed test with a p level of 0.05.
Calculate pooled variance, s²_pooled.
Calculate the variance version of standard error for each group.
Calculate the variance and the standard deviation of the distribution of differences between means.
Calculate the t statistic.
Calculate the 95% confidence interval.
Calculate Cohen’s d.

Question 10.20

10.20

Consider the following data from two independent groups:

Liberals: 2, 1, 3, 2

Conservatives: 4, 3, 3, 5, 2, 4

Calculate s² for each group.
Calculate df_X, df_Y, and df_total.
Determine the critical values for t, assuming a two-tailed test with a p level of 0.05.
Calculate pooled variance, s²_pooled.
Calculate the variance version of standard error for each group.
Calculate the variance and the standard deviation of the distribution of differences between means.
Calculate the t statistic.
Calculate the 95% confidence interval.
Calculate Cohen’s d.

Question 10.21

10.21

Find the critical t values for the following data sets:

268

Group 1 has 21 participants and group 2 has 16 participants. You are performing a two-tailed test with a p level of 0.05.
You studied 3-year-old children and 6-year-old children, with samples of 12 and 16, respectively. You are performing a two-tailed test with a p level of 0.01.
You have a total of 17 degrees of freedom for a two-tailed test and a p level of 0.10.

Applying the Concepts

Question 10.22

10.22

Making a decision: Numeric results for several independent-samples t tests are presented here. Decide whether each test is statistically significant, and report each result in the standard APA format.

A total of 73 people were studied, 40 in one group and 33 in the other group. The test statistic was calculated as 2.13 for a two-tailed test with a p level of 0.05.
One group of 23 people was compared to another group of 18 people. The t statistic obtained for their data was 1.77. Assume you were performing a two-tailed test with a p level of 0.05.
One group of nine mice was compared to another group of six mice, using a two-tailed test at a p level of 0.01. The test statistic was calculated as 3.02.

Question 10.23

10.23

The independent-samples t test, hypnosis, and the Stroop effect: Using data from Exercise 9.53 on the effects of posthypnotic suggestion on the Stroop effect (Raz, Fan, & Posner, 2005), let’s conduct an independent-samples t test. For this test, we will pretend that two sets of people participated in the study, a between-groups design, whereas previously we considered data from a within-groups design. The first score for each original participant will be in the first sample—those not receiving a posthypnotic suggestion. The second score for each original participant will be in the second sample—those receiving a posthypnotic suggestion.

Sample 1: 12.6, 13.8, 11.6, 12.2, 12.1, 13.0

Sample 2: 8.5, 9.6, 10.0, 9.2, 8.9, 10.8

Conduct all six steps of an independent-samples t test. Be sure to label all six steps.
Report the statistics as you would in a journal article.
What happens to the test statistic when you switch from having all participants be in both samples to having two separate samples? Given the same numbers, is it easier to reject the null hypothesis with a within-groups design or with a between-groups design?
In your own words, why do you think it is easier to reject the null hypothesis in one of these situations than in the other?
Calculate the 95% confidence interval.
State in your own words what we learn from this confidence interval.
What information does the confidence interval give us that we also get from the hypothesis test?
What additional information does the confidence interval give us that we do not get from the hypothesis test?
Calculate the appropriate measure of effect size.
Based on Cohen’s conventions, is this a small, medium, or large effect size?
Why is it useful to have this information in addition to the results of a hypothesis test?

Question 10.24

10.24

An independent-samples t test and getting ready for a date: In an example we sometimes use in our statistics classes, several semesters’ worth of male and female students were asked how long, in minutes, they spend getting ready for a date. The data reported below reflect the actual means and the approximate standard deviations for the actual data from 142 students.

Men: 28, 35, 52, 14

Women: 30, 82, 53, 61

Conduct all six steps of an independent-samples t test. Be sure to label all six steps.
Report the statistics as you would in a journal article.
Calculate the 95% confidence interval.
Calculate the 90% confidence interval.
How are the confidence intervals different from each other? Explain why they are different.
Calculate the appropriate measure of effect size.
Based on Cohen’s conventions, is this a small, medium, or large effect size?
Why is it useful to have this information in addition to the results of a hypothesis test?

Question 10.25

10.25

An independent-samples t test, gender, and talkativeness: “Are Women Really More Talkative Than Men?” is the title of an article that appeared in the journal Science. In the article, Mehl, Vazire, Ramirez-Esparza, Slatcher, & Pennebaker (2007) report the results of a study of 396 men and women. Each participant wore a microphone that recorded every word he or she uttered. The researchers counted the number of words uttered by men and women and compared them. The data below are fictional but they re-create the pattern that Mehl and colleagues observed:

Men: 16,345 17,222 15,646 14,889 16,701

Women: 17,345 15,593 16,624 16,696 14,200

Conduct all six steps of an independent-samples t test. Be sure to label all six steps.
Report the statistics as you would in a journal article.
Calculate the 95% confidence interval.
Express the confidence interval in writing, according to the format discussed in the chapter.
State in your own words what we learn from this confidence interval.
Calculate the appropriate measure of effect size.
Based on Cohen’s conventions, is this a small, medium, or large effect size?
Why is it useful to have this information in addition to the results of a hypothesis test?

269

Question 10.26

10.26

An independent-samples t test, “all inclusive” resorts, and alcohol consumption: At some vacation destinations, “all-inclusive” resorts allow you to pay a flat rate and then eat and drink as much as you want. There has been concern about whether these deals might lead to excessive consumption of alcohol by young adults on spring break trips. You decide to spend your spring break collecting data on this issue. Of course, you need to take all of your friends on this funded research trip, because you need a lot of research assistants! You collect data on the number of drinks consumed in a day by people staying at all-inclusive resorts and by those staying at noninclusive resorts. Your data include the following:

All-inclusive resort guests: 10, 8, 13

Noninclusive resort guests: 3, 15, 7

Conduct all six steps of an independent-samples t test. Be sure to label all six steps.
Report the statistics as you would in a journal article.
Is there a shortcut you could or did use to compute your hypothesis test? (Hint: There are equal numbers of participants in the two groups.)
Calculate the 95% confidence interval.
State in your own words what we learn from this confidence interval.
Express the confidence interval, in a sentence, as a margin of error.
Calculate the appropriate measure of effect size.
Based on Cohen’s conventions, is this a small, medium, or large effect size?
Why is it useful to have this information in addition to the results of a hypothesis test?

Question 10.27

10.27

An independent-samples t test and “mother hearing”: Some people claim that women can experience “mother hearing,” an increased sensitivity to and awareness of noises, in particular those of children. This special ability is often associated with being a mother, rather than simply with being female. Using hypothetical data, let’s put this idea to the test. Imagine we recruit women to come to a sleep experiment where they think they are evaluating the comfort of different mattresses. While they are asleep, we introduce noises to test the minimum volume needed for the women to be awakened by the noise. Here are the data in decibels (dB):

Mothers: 33, 55, 39, 41, 67

Nonmothers: 56, 48, 71

Conduct all six steps of an independent-samples t test. Be sure to label all six steps.
Report the statistics as you would in a journal article.
Calculate the 95% confidence interval.
State in your own words what we learn from this confidence interval.
Explain why interval estimates are better than point estimates.
Calculate the appropriate measure of effect size.
Based on Cohen’s conventions, is this a small, medium, or large effect size?
Why is it useful to have this information in addition to the results of a hypothesis test?

Question 10.28

10.28

Choosing a hypothesis test: For each of the following three scenarios, state which hypothesis test you would use from among the four introduced so far: the z test, the single-sample t test, the paired-samples t test, and the independent-samples t test. (Note: In the actual studies described, the researchers did not always use one of these tests, often because the actual experiment had additional variables.) Explain your answer.

A study of 40 children who had survived a brain tumor revealed that the children were more likely to have behavioral and emotional difficulties than were children who had not experienced such a trauma (Upton & Eiser, 2006). Parents rated children’s difficulties, and the ratings data were compared with known means from published population norms.
Talarico and Rubin (2003) recorded the memories of 54 students just after the terrorist attacks in the United States on September 11, 2001—some memories related to the terrorist attacks on that day (called flashbulb memories for their vividness and emotional content) and some everyday memories. They found that flashbulb memories were no more consistent over time than everyday memories, even though they were perceived to be more accurate.
The HOPE VI Panel Study (Popkin & Woodley, 2002) was initiated to test a U.S. program aimed at improving troubled public housing developments. Residents of five HOPE VI developments were examined at the beginning of the study so researchers could later ascertain whether their quality of life had improved. Means at the beginning of the study were compared to known national data sources (e.g., the U.S. Census, the American Housing Survey) that had summary statistics, including means and standard deviations.

270

Question 10.29

10.29

Taylor and Ste-Marie (2001) studied eating disorders in 41 Canadian female figure skaters. They compared the figure skaters’ data on the Eating Disorder Inventory to the means of known populations, including women with eating disorders. On average, the figure skaters were more similar to the population of women with eating disorders than to those without eating disorders.
In an article titled “A Fair and Balanced Look at the News: What Affects Memory for Controversial Arguments,” Wiley (2005) found that people with a high level of previous knowledge about a given controversial topic (e.g., abortion, military intervention) had better average recall for arguments on both sides of that issue than did those with lower levels of knowledge.
Engle-Friedman and colleagues (2003) studied the effects of sleep deprivation. Fifty students were assigned to one night of sleep loss (students were required to call the laboratory every half-hour all night) and then one night of no sleep loss (normal sleep). The next day, students were offered a choice of math problems with differing levels of difficulty. Following sleep loss, students tended to choose less challenging problems.

Question 10.30

10.30

Null and research hypotheses: Using the research studies described in the previous exercise, create null hypotheses and research hypotheses appropriate for the chosen statistical test:

Taylor and Ste-Marie (2001) studied eating disorders in 41 Canadian female figure skaters. They compared the figure skaters’ data on the Eating Disorder Inventory to the means of known populations, including women with eating disorders. On average, the figure skaters were more similar to the population of women with eating disorders than to those without eating disorders.
In an article titled “A Fair and Balanced Look at the News: What Affects Memory for Controversial Arguments,” Wiley (2005) found that people with a high level of previous knowledge about a given controversial topic (e.g., abortion, military intervention) had better average recall for arguments on both sides of that issue than did those with lower levels of knowledge.
Engle-Friedman and colleagues (2003) studied the effects of sleep deprivation. Fifty students were assigned to one night of sleep loss (students were required to call the laboratory every half-hour all night) and then one night of no sleep loss (normal sleep). The next day, students were offered a choice of math problems with differing levels of difficulty. Following sleep loss, students tended to choose less challenging problems.

Question 10.31

10.31

Independent-samples t test and walking speed: The New York City Department of City Planning (2006) studied pedestrian walking speeds. The report stated that pedestrians who were en route to work walked a median of 4.41 feet per second, whereas tourist pedestrians walked a median of 3.79 feet per second. They did not report results of any hypothesis tests.

Why would an independent-samples t test be appropriate in this situation?
What would the null hypothesis and research hypothesis be in this situation?

Question 10.32

10.32

Independent-sample t tests and the “fun theory”: Volkswagen has created a series of videos based on its “fun theory,” the idea that you can change behavior if you take an activity that is good for society and make it fun. (You can watch the videos at http://www.thefuntheory.com/.) For each of the following examples, state the independent variable (and its levels) as well as the dependent variable (and the types of variables that both of these are). Then, state whether you could use an independent-samples t test to analyze the data, and explain your answer.

A “Speed Camera Lottery”—in which an electronic sign told people how fast they were going so they could adjust their speed—was introduced. As people passed the electronic sign, a camera took a photo of their license plate. If they were speeding, they were mailed a ticket and had to pay a fine. If they were obeying the speed limit, they were entered into a lottery to win some of the money from those who paid speeding tickets. The average speed using the Speed Camera Lottery sign was 25 kilometers per hour, and the average speed with no lottery sign was 32 kilometers per hour.
At the exit of a subway station, stairs and an escalator were side by side. The stairs were turned into a piano, so that when you climbed them, you heard musical notes. While the Piano Staircase was in place, 66% more people took the stairs—rather than the escalator—than when the Piano Staircase was not in place.
A trash bin was designed so that when someone threw trash into it, there was a long whistling sound, followed by a thud, as if the trash were falling into an extremely deep bin. When the bin was used, an average of 72 kg of trash was disposed of in a day; when it was not used, an average of 31 kg of trash was disposed of in a day.

Question 10.33

10.33

Cafeteria trays, food consumption, and an independent-samples t test: Kiho Kim and Stevia Morawski (2012) reported the following in the abstract (brief summary) of their published research study: “Here, we report on the results of an experiment to evaluate the effects of tray availability on food waste production and dish use in a university dining facility. We sampled 360 individual diners over a 6-day period and documented a 32% reduction in food waste and a 27% reduction in dish use when trays were unavailable.”

271

What was the independent variable and what were its levels?
What were the dependent variables? How did the researchers likely operationalize their variables?
The researchers describe their study as an experiment. Explain what they mean by this.
Why would it be possible to use independent-samples t tests to analyze the data from their study?

Question 10.34

10.34

Independent-sample t tests and “Blinded with Science”: Researchers studied the effects of learning about the effectiveness of a new medication (Tal & Wansink, 2014). Some participants heard information about the medication; others heard the same information and saw a graph that depicted the data they had heard about. Thus, the two groups had identical information. Participants rated the effectiveness of the medication on a scale of 1–9, with 9 indicating a higher level of effectiveness. The researchers reported “Participants given graphs expressed greater belief in the claims, rating the medication as more effective (6.83 of 9) than did participants given verbal description only (6.12 of 9): t(59) = −2.1, p = .04” (p. 4). The researchers titled their paper “Blinded with Science” because the mere presence of a scientific cue—a graph—altered perceptions of the medication.

What kind of t test did the researchers use? Explain your answer.
How do we know this finding is statistically significant?
How many participants were in this experiment?
Identify the means of the two groups.
What additional statistics would it have been helpful for the researchers to include?

Question 10.35

10.35

Independent-sample t tests and note-taking—laptop or longhand: Researchers explored whether there were mean differences between students who were randomly assigned to take notes longhand and students who were randomly assigned to take notes on their laptops (Mueller & Oppenheimer, 2014). They had observed that students who took notes by hand performed better, on average, on conceptual questions—those that involved thinking beyond just recalling facts—than students who took notes on their laptops. To explore reasons for this difference, they examined the students’ notes. The researchers “found that laptop notes contained an average of 14.6% verbatim overlap with the lecture (SD = 7.3%), whereas longhand notes averaged only 8.8% (SD = 4.8%), t(63) = −3.77, p < .001, d = 0.94” (p. 3). They concluded that when people took notes longhand, they were more likely to put ideas in their own words, which likely led to deeper processing and better learning of information.

What kind of t test did the researchers use? Explain your answer.
How do we know this finding is statistically significant?
How many participants were in this experiment?
Identify the means of the two groups.
What is the effect size for this finding? Interpret what that means in terms of Cohen’s conventions.

Putting It All Together

Question 10.36

10.36

Gender and number words: Chang, Sandhofer, and Brown (2011) wondered whether mothers used number words more, on average, with their preschool sons than with their preschool daughters. Each participating family included one mother and one child—either female or male. They speculated that early exposure to more number words might predispose children to like mathematics. They reported the following: “An independent-samples t test revealed statistically significant differences in the percentages of overall numeric speech used when interacting with boys compared with girls, t(30) = 2.40, p < .05, d = .88. That is, mothers used number terms with boys an average of 9.49% of utterances (SD = 6.78%) compared with 4.64% of utterances with girls (SD = 4.43%)” (pp. 444–445).

Is this a between-groups or within-groups design? Explain your answer.
What is the independent variable? What is the dependent variable?
How many children were in the total sample? Explain how you determined this.
Is the sample likely randomly selected? Is it likely that the researchers used random assignment?
Were the researchers able to reject the null hypothesis? Explain.
What can you say about the size of the effect?
Describe how you could design an experiment to test whether exposure to more number words in preschool leads children to like mathematics more when they enter school.

Question 10.37

10.37

School lunches: Alice Waters, owner of the Berkeley, California, restaurant Chez Panisse, has long been an advocate for the use of simple, fresh, organic ingredients in home and restaurant cooking. She has also turned her considerable expertise to school cafeterias. Waters (2006) praised changes in school lunch menus that have expanded nutritious offerings, but she hypothesizes that students are likely to circumvent healthy lunches by avoiding vegetables and smuggling in banned junk food unless they receive accompanying nutrition education and hands-on involvement in their meals. She has spearheaded an Edible Schoolyard program in Berkeley, which involves public school students in the cultivation and preparation of fresh foods, and states that such interactive education is necessary to combat growing levels of childhood obesity. “Nothing less,” Waters writes, “will change their behavior.”

272

In your own words, what is Waters predicting? Citing the confirmation bias, explain why Waters’ program, although intuitively appealing, should not be instituted nationwide without further study.
Describe a simple between-groups experiment with a nominal independent variable with two levels and a scale-dependent variable to test Waters’ hypothesis. Specifically identify the independent variable, its levels, and the dependent variable. State how you will operationalize the dependent variable.
Which hypothesis test would be used to analyze this experiment? Explain your answer.
Conduct step 1 of hypothesis testing.
Conduct step 2 of hypothesis testing.
State at least one other way you could operationalize the dependent variable.
Let’s say, hypothetically, that Waters discounted the need for the research you propose by citing her own data that the Berkeley school in which she instituted the program has lower rates of obesity than other California schools. Describe the flaw in this argument by discussing the importance of random selection and random assignment.

Question 10.38

10.38

Perception and portion sizes: Researchers at the Cornell University Food and Brand Lab conducted an experiment at a fitness camp for adolescents (Wansink & van Ittersum, 2003). Campers were given either a 22-ounce glass that was tall and thin or a 22-ounce glass that was short and wide. Campers with the short glasses tended to pour more soda, milk, or juice than campers with the tall glasses.

Is it likely that the researchers used random selection? Explain.
Is it likely that the researchers used random assignment? Explain.
What is the independent variable, and what are its levels?
What is the dependent variable?
Which hypothesis test would the researchers use? Explain.
Conduct step 1 of hypothesis testing.
Conduct step 2 of hypothesis testing.
How could the researchers redesign this study so that they could use a paired-samples t test?