Exercises

Clarifying the Concepts

314

Question 11.1

11.1

What is an ANOVA?

Question 11.2

11.2

What do the F distributions allow us to do that the t distributions do not?

Question 11.3

11.3

The F statistic is a ratio of between-groups variance and within-groups variance. What are these two types of variance?

Question 11.4

11.4

What is the difference between a within-groups ­(repeated-measures) ANOVA and a between-groups ANOVA?

Question 11.5

11.5

What are the three assumptions for a between-groups ANOVA?

Question 11.6

11.6

The null hypothesis for ANOVA posits no difference among population means, as in other hypothesis tests, but the research hypothesis in this case is a bit different. Why?

Question 11.7

11.7

Why is the F statistic always positive?

Question 11.8

11.8

In your own words, define the word source as you would use it in everyday conversation. Provide at least two different meanings that might be used. Then define the word as a statistician would use it.

Question 11.9

11.9

Explain the concept of sum of squares.

Question 11.10

11.10

The total sum of squares for a one-way between-groups ANOVA is found by adding which two statistics together?

Question 11.11

11.11

What is the grand mean?

Question 11.12

11.12

How do we calculate the between-groups sum of squares?

Question 11.13

11.13

What do we typically use to measure effect size for a z test or a t test? What do we use to measure effect size for an ANOVA?

Question 11.14

11.14

What are Cohen’s conventions for interpreting effect size using R2?

Question 11.15

11.15

What does post hoc mean, and when are these tests needed with ANOVA?

Question 11.16

11.16

Define the symbols in the following formula: image

Question 11.17

11.17

Find the error in the statistics language in each of the following statements about z, t, or F distributions or their related tests. Explain why it is incorrect and ­provide the correct word.

  1. The professor reported the mean and standard error for the final exam in the statistics class.

  2. Before we can calculate a t statistic, we must know the population mean and the population standard deviation.

  3. The researcher calculated the parameters for her three samples so that she could calculate an F ­statistic and conduct an ANOVA.

  4. For her honors project, Evelyn calculated a z statistic so that she could compare the mean video game scores of a sample of students who had ingested caffeine with a sample of students who had not ingested caffeine.

Question 11.18

11.18

Find the incorrectly used symbol or symbols in each of the following statements or formulas. For each statement or formula, (i) state which symbol(s) is/are used incorrectly, (ii) explain why the symbol(s) in the original statement is/are incorrect, and (iii) state which symbol(s) should be used.

  1. When calculating an F statistic, the numerator includes the estimate for the between-groups variance, s.

  2. SSbetween = (X − GM)2

  3. SSwithin = (X − M)

  4. image

Question 11.19

11.19

What are the four assumptions for a within-groups ANOVA?

Question 11.20

11.20

What are order effects?

Question 11.21

11.21

Explain the source of variability called “subjects.”

Question 11.22

11.22

What is the advantage of the design of the within-groups ANOVA over that of the between-groups ANOVA?

Question 11.23

11.23

What is counterbalancing?

Question 11.24

11.24

Why is it appropriate to counterbalance when using a within-groups design?

Question 11.25

11.25

How do we calculate the sum of squares for subjects?

Question 11.26

11.26

How is the calculation of dfwithin different in a between-groups ANOVA from the calculation in a within-groups ANOVA?

Question 11.27

11.27

How could we turn a between-groups study into a within-groups study?

Question 11.28

11.28

What are some situations in which it might be ­impossible—or not make sense—to turn a between-groups study into a within-groups study?

Question 11.29

11.29

How is the calculation of effect size different for a one-way between-groups ANOVA versus a one-way within-groups ANOVA?

Calculating the Statistics

Question 11.30

11.30

For the following data, assuming a between-groups design, determine:

Group 1: 11, 17, 22, 15

Group 2: 21, 15, 16

Group 3: 7, 8, 3, 10, 6, 4

Group 4: 13, 6, 17, 27, 20

315

  1. dfbetween

  2. dfwithin

  3. dftotal

  4. The critical value, assuming a p value of 0.05

  5. The mean for each group and the grand mean

  6. The total sum of squares

  7. The within-groups sum of squares

  8. The between-groups sum of squares

  9. The rest of the ANOVA source table for these data

  10. Tukey HSD values

Question 11.31

11.31

For the following data, assuming a between-groups design, determine:

1990: 45, 211, 158, 74

2000: 92, 128, 382

2010: 273, 396, 178, 248, 374

  1. dfbetween

  2. dfwithin

  3. dftotal

  4. The critical value, assuming a p value of 0.05

  5. The mean for each group and the grand mean

  6. The total sum of squares

  7. The within-groups sum of squares

  8. The between-groups sum of squares

  9. The rest of the ANOVA source table for these data

  10. The effect size and an indication of its size

Question 11.32

11.32

Calculate the F statistic, writing the ratio accurately, for each of the following cases:

  1. Between-groups variance is 29.4 and within-groups variance is 19.1

  2. Within-groups variance is 0.27 and between-groups variance is 1.56

  3. Between-groups variance is 4595 and within-groups variance is 3972

Question 11.33

11.33

Calculate the F statistic, writing the ratio accurately, for each of the following cases:

  1. Between-groups variance is 321.83 and within-groups variance is 177.24

  2. Between-groups variance is 2.79 and within-groups variance is 2.20

  3. Within-groups variance is 41.60 and between-groups variance is 34.45

Question 11.34

11.34

An incomplete one-way between-groups ANOVA source table is shown below. Compute the missing values.

Source SS df MS F
Between 191.450 — 47.863 —
Within 104.720 32 —
Total — 36

Question 11.35

11.35

An incomplete one-way between-groups ANOVA source table is shown below. Compute the missing values.

Source SS df MS F
Between — 2 — —
Within 89 11 —
Total 132 —

Question 11.36

11.36

Each of the following is a calculated F statistic with its degrees of freedom. Using the F table, estimate the level of significance for each. You can do this by indicating whether its likelihood of occurring is greater than or less than a p level shown on the table.

  1. F = 4.11, with 3 dfbetween and 30 dfwithin

  2. F = 1.12, with 5 dfbetween and 83 dfwithin

  3. F = 2.28, with 4 dfbetween and 42 dfwithin

Question 11.37

11.37

A researcher designs an experiment in which the single independent variable has four levels. If the researcher performed an ANOVA and rejected the null hypothesis, how many post hoc comparisons would she make (assuming she was making all possible comparisons)?

Question 11.38

11.38

A researcher designs an experiment in which the single independent variable has five levels. If the researcher performed an ANOVA and rejected the null hypothesis, how many post hoc comparisons would he make (assuming he was making all possible comparisons)?

Question 11.39

11.39

For the following data, assuming a within-groups design, determine:

Person
1 2 3 4
Level 1 of the independent variable 7 16 3 9
Level 2 of the independent variable 15 18 18 13
Level 3 of the independent variable 22 28 26 29

  1. dfbetween = Ngroups − 1

  2. dfsubjects = n − 1

  3. dfwithin = (dfbetween)(dfsubjects)

  4. dftotal = dfbetween + dfsubjects + dfwithin, or dftotal = Ntotal − 1

  5. SStotal = ∑(X − GM)2

  6. SSbetween = ∑(M − GM)2

  7. SSsubjects = ∑(Mparticipant − GM)2

  8. SSwithin = SStotal − SSbetween − SSsubjects

  9. The rest of the ANOVA source table for these data

    316

  10. The effect size

  11. The Tukey HSD statistic for the comparisons between level 1 and level 3

Question 11.40

11.40

For the following data, assuming a within-groups design, determine:

Person
1 2 3 4 5 6
Level 1 5 6 3 4 2 5
Level 2 6 8 4 7 3 7
Level 3 4 5 2 4 0 4

  1. dfbetween = Ngroups − 1

  2. dfsubjects = n − 1

  3. dfwithin = (dfbetween)(dfsubjects)

  4. dftotal = dfbetween + dfsubjects + dfwithin, or dftotal = Ntotal − 1

  5. SStotal = ∑(X − GM)2

  6. SSbetween = ∑(M − GM)2

  7. SSsubjects = ∑(Mparticipant − GM)2

  8. SSwithin = SStotal − SSbetween − SSsubjects

  9. The rest of the ANOVA source table for these data

  10. The critical F value and your decision about the null hypothesis.

  11. If appropriate, the Tukey HSD statistic for all ­possible mean comparisons

  12. The critical q value; then, make a decision for each comparison in part (k)

  13. The effect size

Question 11.41

11.41

For the following incomplete source table below for a one-way within-groups ANOVA:

Source SS df MS F
Between 941.102 2 — —
Subjects 3807.322 — — —
Within — 20 —
Total 5674.502 —

  1. Complete the missing information.

  2. Calculate R2.

Question 11.42

11.42

Assume that a researcher had 14 individuals participate in all three conditions of her experiment. Use this information to complete the source table below.

Source SS df MS F
Between 60 — — —
Subjects — — — —
Within 50 — —
Total 136 —

Applying the Concepts

Question 11.43

11.43

Comedy versus news and hypothesis testing: Focusing on coverage of the U.S. presidential election, Julia R. Fox, a telecommunications professor at Indiana University, wondered whether The Daily Show, despite its comedy format, was a valid source of news. She coded a number of half-hour episodes of The Daily Show as well as a number of half-hour episodes of the network news (Indiana University Media Relations, 2006). Fox reported that the average amounts of “video and audio substance” were not statistically significantly different between the two types of shows. Her analyses are described as “second by second,” so, for this exercise, assume that all outcome variables are measures of time.

  1. As the study is described, what are the independent and dependent variables? For nominal variables, state the levels.

  2. As the study is described, what type of hypothesis test would Fox use?

  3. Now imagine that Fox added a third category, a cable news channel such as CNN. Based on this new information, state the independent variable or variables and the levels of any nominal independent variables. What hypothesis test would she use?

Question 11.44

11.44

The comparison distribution: For each of the ­following situations, state whether the distribution of interest is a z distribution, a t distribution, or an F ­distribution. Explain your answer.

  1. A city employee locates a U.S. Census report that includes the mean and standard deviation for income in the state of Wyoming and then takes a random sample of 100 residents of the city of Cheyenne. He wonders whether residents of Cheyenne earn more, on average, than Wyoming residents as a whole.

  2. A researcher studies the effect of different contexts on work interruptions. Using discreet video cameras, she observes employees working in enclosed offices in the workplace, in open cubicles in the workplace, and in home offices.

  3. An honors student wondered whether an education in statistics reduces the tendency to believe advertising that cites data. He compares social science majors who had taken statistics and social science majors who had not taken statistics with respect to their responses to an interactive advertising assessment.

Question 11.45

11.45

The comparison distribution: For each of the ­following situations, state whether the distribution of interest is a z distribution, a t distribution, or an F ­distribution. Explain your answer.

  1. A student reads in her Introduction to Psychology textbook that the mean IQ is 100. She asks 10 friends what their IQ scores are (they attend a university that assesses everyone’s IQ score) to determine whether her friends are smarter than average.

    317

  2. Is the presence of books in the home a marker of a stable family? A social worker counted the number of books on view in the living rooms of all the families he visited over the course of one year. He categorized families into four groups: no books visible, only children’s books visible, only adult books visible, and both children’s and adult books visible. The department for which he worked had stability ratings for each family based on a number of measures.

  3. Which television show leads to more learning? A researcher assessed the vocabularies of a sample of children randomly assigned to watch Sesame Street as much as they wanted for a year but to not watch The Wiggles. She also assessed the vocabularies of a sample of children randomly assigned to watch The Wiggles as much as they wanted for a year but not to watch Sesame Street. She compared the average vocabulary scores for the two groups.

Question 11.46

11.46

Links among distributions: The z, t, and F distributions are closely linked. In fact, it is possible to use an F distribution in all cases in which a t or a z could be used.

  1. If you calculated an F statistic of 4.22 but you could have used a t statistic (i.e., the situation met all criteria for using a t statistic), what would the t statistic have been? Explain your answer.

  2. If you calculated an F statistic of 4.22 but you could have used a z statistic, what would the z statistic have been? Explain your answer.

  3. If you calculated a t statistic of 0.67 but you could have used a z statistic, what would the z statistic have been? Explain your answer.

  4. Cite two reasons that all three types of distributions (i.e., z, t, and F) are still in use when we really only need an F distribution.

Question 11.47

11.47

International students and type of ANOVA: Catherine Ruby, a doctoral student at New York University, conducted an online survey to ascertain the reasons that international students chose to attend graduate school in the United States. One of several dependent variables that she considered was reputation; students were asked to rate the importance in their decision of factors such as the reputation of the institution, the institution and program’s academic accreditations, and the reputation of the faculty. Students rated factors on a 1–5 scale, and then all reputation ratings were averaged to form a summary score for each respondent. For each of the following scenarios, state the independent variable with its levels (the dependent variable is reputation in all cases). Then state what kind of an ANOVA she would use.

  1. Ruby compared the importance of reputation among graduate students in different types of programs: arts and sciences, education, law, and business.

  2. Imagine that Ruby followed these graduate ­students for 3 years and assessed their rating of reputation once a year.

  3. Ruby compared international students working toward a master’s, a doctoral, or a professional degree (e.g., MBA) on reputation.

  4. Imagine that Ruby followed international students from their master’s program to their doctoral program to their postdoctoral fellowship, assessing their ratings of reputation once at each level of their training.

Question 11.48

11.48

Type of ANOVA in study of remembering names: Do people remember names better under different circumstances? In a fictional study, a cognitive psychologist studied memory for names after a group activity that lasted 20 minutes. Participants were not told that this was a study of memory. After the group activity, participants were asked to name the other group members. The researcher randomly assigned 120 participants to one of three conditions: (1) group members introduced themselves once (one introduction only), (2) group members were introduced by the experimenter and by themselves (two introductions), and (3) group members were introduced by the experimenter and themselves and also wore name tags throughout the group activity (two introductions and name tags).

  1. Identify the type of ANOVA that should be used to analyze the data from this study.

  2. State what the researcher could do to redesign this study so it would be analyzed with a one-way within-groups ANOVA. Be specific.

Question 11.49

11.49

Political party and ANOVA: Researchers asked 180 U.S. students to identify their political viewpoint as most similar to that of the Republicans, most similar to that of the Democrats, or neither. All three groups then completed a religiosity scale. The researchers wondered whether political orientation affected levels of religiosity, a measure that assesses how religious one is, regardless of the specific religion with which a person identifies.

  1. What is the independent variable, and what are its levels?

  2. What is the dependent variable?

  3. What are the populations and what are the samples?

  4. Would you use a between-groups or within-groups ANOVA? Explain.

  5. Using this example, explain how you would calculate the F statistic.

Question 11.50

11.50

Exercise and the Tukey HSD test: In How It Works 11.1, we conducted a one-way between-groups ANOVA on an abbreviated data set from research by Irwin and colleagues (2004) on adherence to an exercise regimen. Participants were asked to attend a monthly group education program to help them change their exercise behavior. Attendance was taken and ­participants were divided into three categories: those who attended fewer than 5 sessions, those who attended between 5 and 8 sessions, and those who attended between 9 and 12 sessions. The dependent variable was number of minutes of exercise per week. Here are the data once again:

318

< 5 sessions: 155, 120, 130

5–8 sessions: 199, 160, 184

9–12 sessions: 230, 214, 195, 209

  1. What conclusion did we draw in step 6 of the ANOVA? Why could you not be more specific in your conclusion? That is, why is an additional test necessary when the ANOVA is statistically significant?

  2. Conduct a Tukey HSD test for this example. State your conclusions based on this test. Show all calculations.

  3. If we did not reject the null hypothesis for a particular pair of means, then why can’t we conclude that the two means are the same?

Question 11.51

11.51

Grade point average and comparing the t and F distributions: Based on your knowledge of the relation of the t and F distributions, complete the accompanying software output tables. The table for the independent-samples t test and the table for the one-way between-groups ANOVA were calculated using the identical fictional data comparing grade point ­averages (GPAs).

  1. What is the F statistic? Show your calculations. (Hint: The “Mean Square” column includes the two estimates of variance used to calculate the F statistic.)

  2. What is the t statistic? Show your calculations. (Hint: Use the F statistic that you calculated in part (a).)

  3. In statistical software output, “Sig.” refers to the actual p level of the statistic. We can compare the actual p level to a cutoff p level such as 0.05 to decide whether to reject the null hypothesis. For the t test, what is the “Sig.”? Explain how you determined this. (Hint: Would we expect the “Sig.” for the independent-samples t test to be the same as or different from that for the one-way between-groups ANOVA?)

image

Question 11.52

11.52

Consideration of Future Consequences and two kinds of hypothesis testing: Two samples of students, one comprised of social science majors and one comprised of students with other majors, completed the Consideration of Future Consequences scale (CFC). The accompanying tables include the output from software for an independent-samples t test and a one-way between-groups ANOVA on these data.

  1. Demonstrate that the results of the independent-samples t test and the one-way between-groups ANOVA are the same. (Hint: Find the t statistic for the t test and the F statistic for the ANOVA.)

  2. In statistical software output, “Sig.” refers to the actual p level of the statistic. We can compare the actual p level to a cutoff p level such as 0.05 to decide whether to reject the null hypothesis. What are the “Sig.” levels for the two tests here—the independent-samples t test and the one-way between-groups ANOVA? Are they the same or different? Explain why this is the case.

  3. In the CFC ANOVA, the column titled “Mean Square” includes the estimates of variance. Show how the F statistic was calculated from two types of variance. (Hint: Look at the far-left column to determine which estimate of variance is which.)

  4. Looking at the table titled “Group Statistics,” how many participants were in each sample?

  5. Looking at the table titled “Group Statistics,” what is the mean CFC score for the social science majors?

319

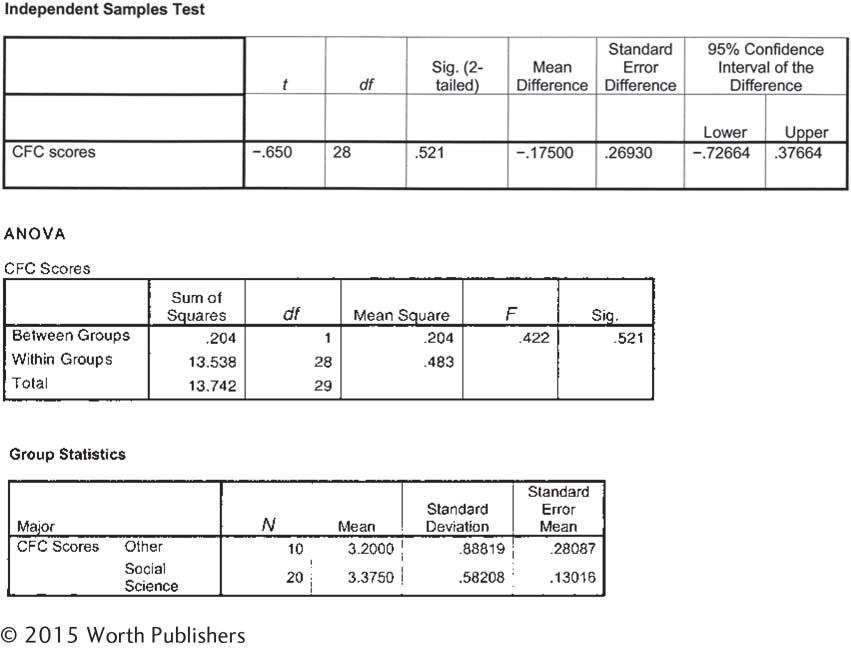
image

Question 11.53

11.53

Instructors on Facebook and one-way ANOVA: Researchers investigated whether the amount of self-disclosure on Facebook affected student perceptions of the instructor, the class, and the classroom environment (Mazer, Murphy, & Simonds, 2007). Students were randomly assigned to view one of three Facebook pages of an instructor. The pages were identical except that one instructor had high self-disclosure, one had medium self-disclosure, and one had low self-disclosure. Self-disclosure was “manipulated in photographs, biological information, and posts” (p. 6). The researchers reported that “Participants who accessed the Facebook website of a teacher high in self-disclosure anticipated higher levels of motivation and affective learning and a more positive classroom climate” (p. 1).

  1. What is the independent variable, what kind of variable is it, and what are its levels?

  2. What is the first dependent variable mentioned, and what kind of variable is this?

  3. Is this a between-groups design or a within-groups design? Explain your answer.

  4. Based on your answers to parts (a) through (c), what kind of ANOVA would the researchers use to analyze the data? Explain your answer.

  5. Is this a true experiment? Explain your answer, and explain what this means for the researchers’ conclusion.

Question 11.54

11.54

Post hoc tests and p values: The most recent version of the Publication Manual of the American Psychological Association (2010) recommends reporting the exact p values for all statistical tests to two decimal places (previously, it recommended reporting p < 0.05 or p > 0.05). Explain how this reporting format allows a reader to more critically interpret the results of post hoc comparisons reported by an author.

Question 11.55

11.55

Post hoc tests, bilingualism, and language skills: Researchers Raluca Barac and Ellen Bialystok (2012) conducted a study in which they compared the language skills of 104 six-year-old children who were in one of four groups. Some children spoke only English. Others were bilingual, speaking English along with Chinese, French, or Spanish. The children completed the Peabody Picture Vocabulary Test (PPVT) as a measure of their vocabulary. An excerpt from the results section of the published journal article follows: “A one-way ANOVA on PPVT scores showed a main effect of language group, F(3, 100) = 8.27, p < .0001. Post hoc [tests] indicated that the monolingual children and the Spanish-English bilingual children outperformed the other two bilingual groups who did not differ from each other.” (Note: When p values are tiny, as in this case, researchers report that they are less than some small value, rather than reporting the exact p value, such as 0.00000038.)

  1. What is the independent variable, what kind of variable is it, and what are its levels? What is the dependent variable and what kind of variable is it?

    320

  2. How do we know that this finding is statistically significant?

  3. Why was the one-way ANOVA not sufficient to draw a conclusion from these data?

  4. Summarize this finding in your own words.

Question 11.56

11.56

Romantic love and post hoc tests: ­Researchers who conducted a study of brain activation and ­romantic love divided their analyses into two groups (Aron et al., 2005). Some analyses—those for which they had ­developed specific hypotheses prior to data ­collection—used a p level of 0.05. The rest of the ­analyses used a p level of 0.001. Explain why the researchers’ plan to have different p levels for the two groups was a wise one.

Question 11.57

11.57

Fear of dogs and one-way within-groups ANOVA: Imagine a researcher wanted to assess people’s fear of dogs as a function of the size of the dog. He assessed fear among people who indicated they were afraid of dogs, using a 30-point scale from 0 (no fear) to 30 (extreme fear). The researcher exposed each participant to three different dogs, a small dog weighing 20 pounds, a medium-sized dog weighing 55 pounds, and a large dog weighing 110 pounds, and assessed the fear level after each exposure. Here are some hypothetical data; note that these are the data from Exercise 11.39, on which you have already calculated numerous statistics:

Person
1 2 3 4
Small dog 7 16 3 9
Medium dog 15 18 18 13
Large dog 22 28 26 29

  1. State the null and research hypotheses.

  2. Determine whether the assumptions of random selection and order effects were met.

  3. In Exercise 11.39, you calculated the effect size for these data. What does this statistic tell us about the effect of size of dog on fear levels?

  4. In Exercise 11.39, you calculated a Tukey HSD test for these data. What can you conclude about the effect of size of dog on fear levels based on this statistic?

Question 11.58

11.58

Chewing-gum commercials and one-way within-groups ANOVA: Commercials for chewing gum make claims about how long the flavor will last. In fact, some commercials claim that the flavor lasts too long, affecting sales and profit. Let’s put these claims to a test. Imagine a student decides to compare four different gums using five participants. Each randomly selected participant was asked to chew a different piece of gum each day for 4 days, such that at the end of the 4 days, each participant had chewed all four types of gum. The order of the gums was randomly determined for each participant. After 2 hours of chewing, participants recorded the intensity of flavor from 1 (not intense) to 9 (very intense). Here are some hypothetical data:

Person
1 2 3 4 5
Gum 1 4 6 3 4 4
Gum 2 8 6 9 9 8
Gum 3 5 6 7 4 5
Gum 4 2 2 3 2 1

  1. Conduct all six steps of the hypothesis test.

  2. Are any additional tests warranted? Explain your answer.

Question 11.59

11.59

Pessimism and one-way within-groups ANOVA: Researchers Busseri, Choma, and Sadava (2009) asked a sample of individuals who scored as pessimists on a measure of life orientation about past, present, and projected future satisfaction with their lives. Higher scores on the life-satisfaction measure indicate higher satisfaction. The data below reproduce the pattern of means that the researchers observed in self-reported life satisfaction of the sample of pessimists for the three time points. Do pessimists predict a gloomy future for themselves?

Person
1 2 3 4 5
Past 18 17.5 19 16 20
Present 18.5 19.5 20 17 18
Future 22 24 20 23.5 21

321

  1. Perform steps 5 and 6 of hypothesis testing. Be sure to complete the source table when calculating the F ratio for step 5.

  2. If appropriate, calculate the Tukey HSD for all ­possible mean comparisons. Find the critical value of q and make a decision regarding the null hypothesis for each of the mean comparisons.

  3. Calculate the R2 measure of effect size for this ANOVA.

Question 11.60

11.60

Pessimism and one-way within-groups ANOVA: The previous exercise describes a study conducted by Busseri and colleagues (2009) using a group of pessimists. These researchers asked the same question of a group of optimists: Optimists rated their past, present, and projected future satisfaction with their lives. Higher scores on the life-satisfaction measure indicate higher satisfaction. The data below reproduce the pattern of means that the researchers observed in self-reported life satisfaction of the sample of optimists for the three time points. Do optimists see a rosy future ahead?

Person
1 2 3 4 5
Past 22 23 25 24 26
Present 25 26 27 28 29
Future 24 27 26 28 29

  1. Perform steps 5 and 6 of hypothesis testing. Be sure to complete the source table when calculating the F ratio for step 5.

  2. If appropriate, calculate the Tukey HSD for all possible mean comparisons. Find the critical value of q and make a decision regarding the null hypothesis for each of the mean comparisons.

  3. Calculate the R2 measure of effect size for this ANOVA.

Question 11.61

11.61

Wagging tails and one-way within-groups ANOVA: How does a dog’s tail wag in response to seeing different people and other pets? Quaranta, Siniscalchi, and Vallortigara (2007) investigated the amplitude and direction of a dog’s tail wagging in response to seeing its owner, an unfamiliar cat, and an unfamiliar dog. The fictional data below are measures of amplitude. These data reproduce the pattern of results in the study, averaging leftward tail wags and rightward tail wags. Use these data to construct the source table for a one-way within-groups ANOVA.

Dog Participant Owner Cat Other Dog
1 69 28 45
2 72 32 43
3 65 30 47
4 75 29 45
5 70 31 44

Question 11.62

11.62

Memory, post hoc tests, and effect size: Luo, Hendriks, and Craik (2007) were interested in whether people might better remember lists of words if the lists were paired with either pictures or sound effects. They asked participants to memorize lists of words under three different learning conditions. In the first ­condition, participants just saw a list of nouns that they were to remember (word-alone condition). In the second condition, the words were also accompanied by a picture of the object (picture condition). In the third condition, the words were accompanied by a sound effect matching the object (sound effect condition). The researchers measured the proportion of words participants got correct in a later recognition test. ­Fictional data from four participants produce results similar to those of the original study. The average proportion of words recognized was M = 0.54 in the word-alone condition, M = 0.69 in the picture condition, and M = 0.838 in the sound effect condition. The source table below depicts the results of the ANOVA on the data from the four fictional participants.

Source SS df MS F
Between 0.177 2 0.089 8.900
Subjects 0.002 3 0.001 0.100
Within 0.059 6 0.010
Total 0.238 11

  1. Is it appropriate to perform post hoc comparisons on the data? Why or why not?

  2. Use the information provided in the ANOVA table to calculate R2. Interpret the effect size using Cohen’s conventions. State what this R2 means in terms of the independent and dependent variables used in this study.

Question 11.63

11.63

Wagging tails, hypothesis-test decision making, and post hoc tests: Assume that we recruited a different sample of five dogs and attempted to replicate the Quaranta and colleagues (2007) study described in Exercise 11.61. The source table for our fictional replication appears below. Find the critical F value and make a decision regarding the null hypothesis. Based on this decision, is it appropriate to conduct post hoc comparisons? Why or why not?

Source SS df MS F
Between 58.133 2 29.067 0.066
Subjects 642.267 4 160.567 0.364
Within 532.533 8 441.567
Total 4232.933 14

Question 11.64

11.64

11.64 Pilots’ mental efforts and a one-way within-groups ANOVA: Researchers examined the amount of mental effort that participants felt they were expending on a cognitively complex task, piloting an unmanned air vehicle (UAV) (Ayaz, Shewokis, Bunce, Izzetoglu, Willems, & Onaral, 2012). The researchers used the Task Load Index (TLX), a measure that assesses participants’ perception of their mental effort following a series of approach and landing tasks in simulated UAV tasks. They wondered whether expertise would have an effect on perceptions of mental effort. In the results section, the researchers reported the results of their analyses, a series of one-way repeated-measures ANOVA. “The results indicated a significant main effect of practice level (beginner/intermediate/advanced conditions) for mental demand (F(2, 8) = 17.87, p < 0.01, η2 = 0.817), effort (F (2, 8) = 16.32, p < 0.01, η2 = 0.803), and frustration (F(2, 8) = 8.60, p < 0.01, η2 = 0.682).” They went on to explain that mental demand, effort, and frustration all tended to decrease with expertise.

322

  1. What is the independent variable in this study?

  2. What are the dependent variables in this study?

  3. Explain why the researchers were able to use a one-way within-groups ANOVA in this situation.

  4. η2 is roughly equivalent to R2. How large are each of these effects, based on Cohen’s conventions?

  5. The researchers drew a specific conclusion beyond that there was some difference, on average, in the dependent variables, depending on the particular levels of the independent variable. What additional test were they likely to have conducted? Explain your answer.

Putting It All Together

Question 11.65

11.65

Trust in leadership and one-way between-groups ANOVA: In Chapter 10, we introduced a study by Steele and Pinto (2006) that examined whether people’s level of trust in their direct supervisor was related to their level of agreement with a policy supported by that leader. Steele and Pinto found that the extent to which subordinates agreed with their supervisor was related to trust and showed no relation to gender, age, time on the job, or length of time working with the supervisor. Let’s assume we used a scale that sorted employees into three groups: low trust, moderate trust, and high trust in supervisors. Below are fictional data regarding level of agreement with a leader’s decision for these three groups. The scores presented are the level of agreement with a decision made by a leader, from 1, the least agreement, to 40, the highest level of agreement. Note: These fictional data are different from those presented in Chapter 10.

Employees with low trust in their leader: 9, 14, 11, 18

Employees with moderate trust in their leader: 14, 35, 23

Employees with high trust in their leader: 27, 33, 21, 34

  1. What is the independent variable? What are its levels?

  2. What is the dependent variable?

  3. Conduct all six steps of hypothesis testing for a one-way between-groups ANOVA.

  4. How would you report the statistics in a journal article?

  5. Conduct a Tukey HSD test. What did you learn?

  6. Why is it not possible to conduct a t test in this situation?

  7. Why is it not possible to use a within-groups design for this study?

Question 11.66

11.66

Orthodontics and one-way between-groups ANOVA: Iranian researchers studied factors affecting patients’ likelihood of wearing orthodontic appliances, noting that orthodontics is perhaps the area of health care with the highest need for patient cooperation (Behenam & Pooya, 2007). Among their analyses, they compared students in primary school, junior high school, and high school. The data that follow have almost exactly the same means as they found in their study, but with far smaller samples. The score for each student is his or her daily hours of wearing the orthodontic appliance.

Primary school: 16, 13, 18

Junior high school: 8, 13, 14, 12

High school: 20, 15, 16, 18

  1. What is the independent variable? What are its levels?

  2. What is the dependent variable?

  3. Conduct all six steps of hypothesis testing for a one-way between-groups ANOVA.

  4. How would you report the statistics in a journal article?

  5. Conduct a Tukey HSD test. What did you learn?

  6. Calculate the appropriate measure of effect size for this sample.

  7. Based on Cohen’s conventions, is this a small, medium, or large effect size?

  8. Why is it useful to know the effect size in addition to the results of a hypothesis test?

  9. How could this study be conducted using a within-groups design?

Question 11.67

11.67

Eye glare, football, and one-way within-groups ANOVA: Does the black grease beneath football players’ eyes really reduce glare or does it just make them look intimidating? In a variation of a study actually conducted at Yale University, 46 participants placed one of three substances below their eyes: black grease, black antiglare stickers, or petroleum jelly. The researchers assessed eye glare using a contrast chart for each participant that gives a value on a scale measure. Every participant was assessed with each of the three substances, one at a time. Black grease led to a reduction in glare compared with the two other conditions, antiglare stickers or petroleum jelly (DeBroff & Pahk, 2003).

Person Black Grease Antiglare Stickers Petroleum Jelly
1 19.8 17.1 15.9
2 18.2 17.2 16.3
3 19.2 18.0 16.2
4 18.7 17.9 17.0

  1. What is the independent variable? What are its levels?

  2. What is the dependent variable?

    323

  3. What kind of ANOVA is this?

  4. What is the first assumption for ANOVA? Is it likely that the researchers met this assumption? Explain your answer.

  5. What is the second assumption for ANOVA? How could the researchers check to see if they had met this assumption? Be specific.

  6. What is the third assumption for ANOVA? How could the researchers check to see if they had met this assumption? Be specific.

  7. What is the fourth assumption, specific to the within-groups ANOVA? What would the researchers need to do to ensure that they meet this assumption?

  8. Perform steps 5 and 6 of hypothesis testing. Be sure to complete the source table when calculating the F ratio for step 5.

  9. If appropriate, calculate the Tukey HSD for all possible mean comparisons. Find the critical value of q and make a decision regarding the null hypothesis for each of the mean comparisons.

  10. Calculate the R2 measure of effect size for this ANOVA.

  11. How could this study be conducted using a between-groups design?

Question 11.68

11.68

ANOVA and taking notes: Researchers studied the type of note-taking that would lead to the best performance on conceptual questions on a test (Mueller & Oppenheimer, 2014). Conceptual questions are those in which students have to apply the material, rather than just answer fact-based questions. Students were randomly assigned to one of the following groups:

  1. Take notes by hand (the longhand group)

  2. Take notes on their laptops as usual (the laptop-nonintervention group)

  3. Take notes on their laptops with instructions to try to put the notes in their own words (the laptop-intervention group)

Because people tend to take notes on their laptops that are verbatim, the researchers speculated that the ­laptop-nonintervention group would lead to less learning, on average, than the other two groups. The researchers reported that “results showed that on ­conceptual-application questions, longhand ­participants performed better (z-score M = 0.28, SD = 1.04) than laptop-nonintervention participants (z-score M = −0.15, SD = 0.85), F(1, 89) = 11.98, p = .017, η2p= .12. Scores for laptop-intervention participants (z-score M = −0.11, SD = 1.02) did not significantly differ from those for either laptop-nonintervention (p = .91) or longhand (p = .29) ­participants” (p. 1162).

  1. What is the independent variable in this study? What are its levels?

  2. What is the dependent variable in this study?

  3. Is this an experiment or a correlational study? Explain your answer.

  4. The report of the statistics provides us with z-score M rather than M. Explain what these researchers are reporting here.

  5. Which groups are significantly different from each other? Describe two ways that we know this.

  6. The effect size is given in terms of η2p. What does this tell us about the effect size? (Note: The subscript p means “partial,” and indicates that this effect size is just for this particular finding. You may ignore the p in your answer. Remember that η2 is roughly equivalent to R2).

  7. A friend hears this finding and says, “I don’t want to take notes longhand, but I’ll think about typing the notes in my own words. The mean z-score of −.11 is higher than the mean z-score of −.15.” Why is this statement problematic from a statistical point of view?

  8. If the finding of no significant difference between the longhand group and the laptop-intervention group is wrong, what kind of error is this? Explain your answer.