How It Works
15.1 CONDUCTING A CHI-
Gary Steinman (2006), an obstetrician and gynecologist, studied whether a woman’s diet could affect the likelihood that she would have twins. Insulin-
Step 1: Population 1: Vegans who recently gave birth, like those whom we observed. Population 2: Vegans who recently gave birth who are like the general population of mostly nonvegans.
The comparison distribution is a chi-
Step 2: Null hypothesis: Vegan women give birth to twins at the same rate as the general population. Research hypothesis: Vegan women give birth to twins at a different rate than the general population.
Step 3: The comparison distribution is a chi-
461
Step 4: The critical chi-
Step 5: Observed (among vegan mothers)
| Singleton | Twins |
| 1038 | 4 |
Expected (based on the 1.9% rate in the general population)
| Singleton | Twins |
| 1022.202 | 19.798 |
| Category | Observed (O) | Expected (E) | O – E | (O – E)2 |
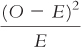
|
| Singleton | 1038 | 1022.202 | 15.798 | 249.577 | 0.244 |
| Twins | 4 | 19.798 | −15.798 | 249.577 | 12.606 |
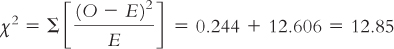
Step 6: Reject the null hypothesis; it appears that vegan mothers are less likely to have twins than are mothers in the general population.
The statistics, as reported in a journal article, would read:
χ2 (1, N = 1042) = 12.85, p < 0.05
15.2 CONDUCTING A CHI-
15.2 CONDUCTING A CHI-
Do people who move far from their hometown have a more exciting life? Since 1972, the General Social Survey (GSS) has asked approximately 40,000 adults in the United States numerous questions about their lives. During several years of the GSS, participants were asked, “In general, do you find life exciting, pretty routine, or dull?” (a variable called LIFE) and “When you were 16 years old, were you living in the same (city/town/country)?” (a variable called MOBILE16). How can we use these data to conduct the six steps of hypothesis testing for a chi-
In this case, there are two nominal variables. The independent variable is where a person lives relative to when he or she was 16 years old (same city, or same state but different city, or different state). The dependent variable is how the person finds life (exciting, routine, dull). Here are the data:
| Exciting | Routine | Dull | |
| Same city | 4890 | 6010 | 637 |
| Same state/different city | 3368 | 3488 | 337 |
| Different state | 4604 | 4139 | 434 |
Step 1: Population 1: People like those in this sample. Population 2: People from a population in which a person’s characterization of life as exciting, routine, or dull does not depend on where that person is living relative to when he or she was 16 years old.
The comparison distribution is a chi-
462
Step 2: Null hypothesis: The proportion of people who find life to be exciting, routine, or dull does not depend on where they live relative to where they lived when they were 16 years old. Research hypothesis: The proportion of people who find life exciting, routine, or dull differs depending on where they live relative to where they lived when they were 16 years old.
Step 3: The comparison distribution is a chi-
dfχ2 = (krow − 1)(kcolumn − 1) = (3 − 1)(3 − 1) = (2)(2) = 4
Step 4: The critical chi-
Step 5:
| Observed (Expected in parentheses) | ||||
| Exciting | Routine | Dull | ||
| Same city | 4890 | 6010 | 637 | 11,537 |
| (5318.557) | (5641.593) | (576.85) | ||
| Same state/different city | 3368 | 3488 | 337 | 7193 |
| (3315.973) | (3517.377) | (359.65) | ||
| Different state | 4604 | 4139 | 434 | 9178 |
| (4231.058) | (4488.042) | (458.90) | ||
| 12,862 | 13,637 | 1408 | 27,907 | |

463
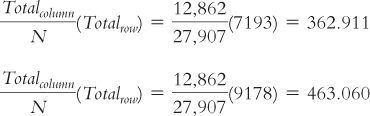
| Category | (O – E)2 |
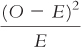
|
| Same city; exciting | 183,661.10 | 34.532 |
| Same city; routine | 135,723.70 | 24.058 |
| Same city; dull | 3618.023 | 6.272 |
| Same state/different city; exciting | 2706.809 | 0.816 |
| Same state/different city; routine | 863.008 | 0.245 |
| Same state/different city; dull | 513.022 | 1.426 |
| Different state; exciting | 139,085.70 | 32.873 |
| Different state; routine | 121,830.30 | 27.146 |
| Different state; dull | 620.01 | 1.351 |
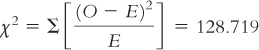
Step 6: Reject the null hypothesis. The calculated chi-
We would present these statistics in a journal article as: χ2(4, N = 27,907) = 128.72, p < 0.05.
15.3 CALCULATING CRAMÉR’S V
15.3 CALCULATING CRAMÉR’S V
What is the effect size, Cramér’s V, for the chi-
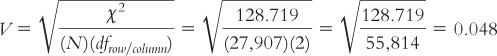
According to Cohen’s conventions, this is a small effect size. With this piece of information, we’d present the statistics in a journal article as:
χ2(4, N = 27,907) = 128.72 < 0.05, Cramér’s V = 0.05
15.4 CALCULATING THE SPEARMAN RANK-
15.4 CALCULATING THE SPEARMAN RANK-
The accompanying table includes ranks for accomplishment-
First, we have to convert the numbers of Olympic medals to ranks. Then we can calculate the correlation coefficient.
464
| Country | Pride Rank | Olympic Medals | Medals Rank | Difference (D) | Squared Difference (D2) |
| United States | 1 | 97 | 1 | 0 | 0 |
| South Africa | 2 | 5 | 7 | −5 | 25 |
| Austria | 3 | 3 | 8 | −5 | 25 |
| Canada | 4 | 14 | 5 | −1 | 1 |
| Chile | 5 | 1 | 10 | −5 | 25 |
| Japan | 6 | 18 | 3 | 3 | 9 |
| Hungary | 7 | 17 | 4 | 3 | 9 |
| France | 8 | 38 | 2 | 6 | 36 |
| Norway | 9 | 10 | 6 | 3 | 9 |
| Slovenia | 10 | 2 | 9 | 1 | 1 |
ΣD2 = (0 + 25 + 25 + 1 + 25 + 9 + 9 + 36 + 9 + 1) = 140
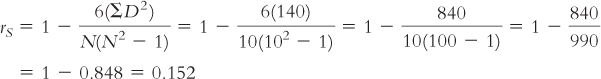
15.5 CONDUCTING THE MANN–
15.5 CONDUCTING THE MANN–
The Mann–
| 1 | Harvard University (E) |
| 2 | Princeton University (E) |
| 3.5 | University of Michigan, Ann Arbor (M) |
| 3.5 | Yale University (E) |
| 5 | Columbia University (E) |
| 6 | Massachusetts Institute of Technology (E) |
| 7 | Duke University (E) |
| 8 | University of Chicago (M) |
| 9.5 | University of North Carolina, Chapel Hill (E) |
| 9.5 | Washington University in St. Louis (M) |
| 12.5 | New York University (E) |
| 12.5 | The Ohio State University (M) |
| 12.5 | University of Rochester (E) |
| 12.5 | University of Wisconsin, Madison (M) |
| 15.5 | Cornell University (E) |
| 15.5 | University of Minnesota, Twin Cities (M) |
| 17 | Northwestern University (M) |
| 18 | University of Illinois, Urbana- |
465
How can we conduct a Mann–
Step 1: This study meets the first and third of the three assumptions: (1) There are ordinal data after we convert the data from scale to ordinal. (2) The researchers did not use random selection, so the ability to generalize beyond this sample is limited. (3) There are some ties, but we will assume that there are not so many as to render the results of the test invalid.
Step 2: Null hypothesis: Political science programs on the East Coast and those in the Midwest do not differ in national ranking. Research hypothesis: Political science programs on the East Coast and those in the Midwest differ in national ranking.
Step 3: There are 10 top political science programs on the East Coast and 8 in the Midwest.
Step 4: The cutoff, or critical value, for a Mann–
Step 5:
| School | Rank | East Coast Rank | Midwest Rank |
| Harvard University | 1 | 1 | |
| Princeton University | 2 | 2 | |
| University of Michigan, Ann Arbor | 3.5 | 3.5 | |
| Yale University | 3.5 | 3.5 | |
| Columbia University | 5 | 5 | |
| Massachusetts Institute of Technology | 6 | 6 | |
| Duke University | 7 | 7 | |
| University of Chicago | 8 | 8 | |
| University of North Carolina, Chapel Hill | 9.5 | 9.5 | |
| Washington University in St. Louis | 9.5 | 9.5 | |
| New York University | 12.5 | 12.5 | |
| The Ohio State University | 12.5 | 12.5 | |
| University of Rochester | 12.5 | 12.5 | |
| University of Wisconsin, Madison | 12.5 | 12.5 | |
| Cornell University | 15.5 | 15.5 | |
| University of Minnesota, Twin Cities | 15.5 | 15.5 | |
| Northwestern University | 17 | 17 | |
| University of Illinois, Urbana- |
18 | 18 |
Before we continue, we sum the ranks for each group and add subscripts to indicate which group is which:
ΣRE = (1 + 2 + 3.5 + 5 + 6 + 7 + 9.5 + 12.5 + 12.5 + 15.5) = 74.5
ΣRM = (3.5 + 8 + 9.5 + 12.5 + 12.5 + 15.5 + 17 + 18) = 96.5
The formula for the first group is:

466
The formula for the second group is:
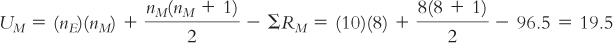
Step 6: For a Mann–
In a journal article, the statistics would read:
U = 19.5, p > 0.05