Exercises

Clarifying the Concepts

Question 2.1

2.1

What are raw scores?

Question 2.2

2.2

What are the steps to create a frequency table?

Question 2.3

2.3

What is the difference between a frequency table and a grouped frequency table?

Question 2.4

2.4

Describe two ways that statisticians might use the word interval.

Question 2.5

2.5

What is the difference between a histogram and a bar graph?

Question 2.6

2.6

What are the typical labels for the x-axis and the y-axis in a histogram?

Question 2.7

2.7

What are the differences between a histogram and a frequency polygon?

Question 2.8

2.8

What is the benefit of creating a visual distribution of data rather than simply looking at a list of the data?

Question 2.9

2.9

In your own words, define the word distribution, first as you would use it in everyday conversation and then as a statistician would use it.

Question 2.10

2.10

What is a normal distribution?

Question 2.11

2.11

How do positively skewed distributions and negatively skewed distributions deviate from a normal distribution?

Question 2.12

2.12

What is a floor effect and how does it affect a distribution?

Question 2.13

2.13

What is a ceiling effect and how does it affect a distribution?

Calculating the Statistics

Question 2.14

2.14

Convert the following to percentages: 63 out of 1264; 2 out of 88.

Question 2.15

2.15

Convert the following to percentages: 7 out of 39; 122 out of 300.

Question 2.16

2.16

Counts are often converted to percentages. Convert 817 out of 22,140 into a percentage. Now convert 4009 out of 22,140 into a percentage. What type of variable (nominal, ordinal, or scale) are these data as counts? What kind of variable are they as percentages?

Question 2.17

2.17

Convert 2 out of 2000 into a percentage. Now convert 60 out of 62 into a percentage.

Question 2.18

2.18

Throughout this book, final answers are reported to two decimal places. Report the following numbers this way: 1888.999; 2.6454; and 0.0833.

Question 2.19

2.19

Report the following numbers to two decimal places: 0.0391; 198.2219; and 17.886.

Question 2.20

2.20

On a test of marital satisfaction, scores could range from 0 to 27.

  1. What is the full range of data, according to the calculation procedure described in this chapter?

    41

  2. What would the interval size be if we wanted six intervals?

  3. List the six intervals.

Question 2.21

2.21

If you have data that range from 2 to 68 and you want seven intervals in a grouped frequency table, what would the intervals be?

Question 2.22

2.22

A grouped frequency table has the following intervals: 30–44, 45–59, and 60–74. If converted into a histogram, what would the midpoints be?

Question 2.23

2.23

Referring to the grouped frequency table in Table 2-6, how many children’s shows received pacing scores of 35 or higher?

Question 2.24

2.24

Referring to the histogram in Figure 2-1, estimate how many countries had between 2 and 10 first- or second-place World Cup finishes.

Question 2.25

2.25

If the average person convicted of murder killed only one person, serial killers would create what kind of skew?

Question 2.26

2.26

Would the data for number of murders by those convicted of the crime be an example of a floor effect or ceiling effect?

Question 2.27

2.27

A researcher collects data on the ages of college students. As you have probably observed, the distribution of age clusters around 19 to 22 years, but there are extremes on both the low end (high school prodigies) and the high end (nontraditional students returning to school).

  1. What type of skew might you expect for such data?

  2. Do the skewed data represent a floor effect or a ceiling effect?

Question 2.28

2.28

If you have a Facebook account, you are allowed to have up to 5000 friends. At that point, Facebook cuts you off, and you have to “unfriend” people to add more. Imagine you collected data from Facebook users at your university about the number of friends each has.

  1. What type of skew might you expect for such data?

  2. Do the skewed data represent a floor effect or ceiling effect?

Applying the Concepts

42

Question 2.29

2.29

Frequency tables, histograms, and the National Survey of Student Engagement: The National Survey of Student Engagement (NSSE) surveys freshmen and seniors about their level of engagement in campus and classroom activities that enhance learning. Hundreds of thousands of students at almost 1000 schools have completed surveys since 1999, when the NSSE was first administered. Among the many questions, students are asked how often they have been assigned a paper of 20 pages or more during the academic year. For a sample of 19 institutions classified as national universities that made their data publicly available through the U.S. News & World Report Web site, here are the percentages of students who said they were assigned between 5 and 10 twenty-page papers:
0 5 3 3 1 10 2
2 3 1 2 4 2 1
1 1 4 3 5

  1. Create a frequency table for these data. Include a third column for percentages.

  2. For what percentage of these schools did exactly 4% of the students report that they wrote between 5 and 10 twenty-page papers that year?

  3. Is this a random sample? Explain your answer.

  4. Create a histogram of grouped data, using six intervals.

  5. In how many schools did 6% or more of the students report that they wrote between 5 and 10 twenty-page papers that year?

How are the data distributed?

Question 2.30

2.30

Frequency tables, histograms, and the Survey of Earned Doctorates: The Survey of Earned Doctorates regularly assesses the numbers and types of doctorates awarded at U.S. universities. It also provides data on the length of time in years that it takes to complete a doctorate. Below is a modified list of this completion-time data, truncated to whole numbers and shortened to make your analysis easier. These data have been collected every 5 years since 1982.
8 8 8 8 8 7 6 7 7 7 7 7
6 6 6 6 6 6 7 8 8 8 8 7
6 6 7 7 7 6 11 13 15 15
14 12 9 10 10 9 9 9

  1. Create a frequency table for these data.

  2. How many schools have an average completion time of 8 years or less?

  3. Is a grouped frequency table necessary? Why or why not?

  4. Describe how these data are distributed.

  5. Create a histogram for these data.

  6. At how many universities did students take, on average, 10 or more years to complete their doctorates?

Question 2.31

2.31

Frequency tables, histograms, polygons, and university acceptance rates: U.S. News & World Report publishes acceptance rates for U.S. universities. Following are the acceptance rates for the top 70 U.S. universities in 2011.
6.3 14.0 8.9 21.6 40.6 51.2 50.5 69.4 42.4 68.3
8.5 12.4 18.0 30.4 31.4 51.3 47.5 49.4 54.6 63.5
7.7 12.8 18.8 25.5 28.0 33.4 38.3 25.0 49.4 56.7
7.0 10.1 24.3 23.0 32.7 46.0 52.4 31.6 44.7 62.8
16.3 18.0 16.4 33.3 40.0 35.5 67.6 43.2 57.9 63.3
9.7 18.4 26.7 39.9 34.6 39.6 46.6 34.5 47.3 61.1
7.1 16.5 18.1 21.9 34.1 45.7 58.4 63.4 63.0 46.6

  1. Create a grouped frequency table for these data.

  2. The data have quite a range, with the highest acceptance rates among the top 70 belonging to Yeshiva University in New York, and the lowest belonging to Harvard University. What research hypotheses come to mind when you examine these data? State at least one research question that these data suggest to you.

  3. Create a grouped histogram for these data. Be careful when determining the midpoints of your intervals!

  4. Create a frequency polygon for these data.

  5. Examine these graphs and give a brief description of the distribution. Are there unusual scores? Are the data skewed, and if so, in which direction?

Question 2.32

2.32

Frequency tables, histograms, and the basketball wins: Here are the number of wins for the 30 U.S. National Basketball Association (NBA) teams for the 2012–2013 NBA season.
60 44 39 29 23 57 50 43 37 27
49 42 37 29 19 56 51 40 33 26
48 42 31 25 18 53 44 40 29 23

  1. Create a grouped frequency table for these data.

  2. Create a histogram based on the grouped frequency table.

  3. Write a summary describing the distribution of these data with respect to shape and direction of any skew.

  4. Here are the numbers of wins for the 8 teams in the National Basketball League (NBL) of Canada. Explain why we would not necessarily need a grouped frequency table for these data.

26 33
20 22
20 18
19 2

Question 2.33

2.33

Types of distributions: Consider these three variables: finishing times in a marathon, number of university dining hall meals eaten in a semester on a three-meal-a-day plan, and scores on a scale of extroversion.

  1. Which of these variables is most likely to have a normal distribution? Explain your answer.

  2. Which of these variables is most likely to have a positively skewed distribution? Explain your answer, stating the possible contribution of a floor effect.

  3. Which of these variables is most likely to have a negatively skewed distribution? Explain your answer, stating the possible contribution of a ceiling effect.

Question 2.34

2.34

Type of frequency distribution and type of graph: For each of the types of data described below, first state how you would present individual data values or grouped data when creating a frequency distribution. Then, state which visual display(s) of data would be most appropriate to use. Explain your answers clearly.

  1. Eye color observed for 87 people

  2. Minutes used on a cell phone by 240 teenagers

  3. Time to complete the London Marathon for the more than 35,000 runners who participate

  4. Number of siblings for 64 college students

Question 2.35

2.35

Number of televisions and a grouped frequency distribution: The Canadian Radio-television and Communications Commission (http://www.crtc.gc.ca/eng/home-accueil.htm) gathers data on the numbers of television sets in Canadian homes. Two percent of homes had no television; 28% had one television; 32% had two televisions; 20% had three televisions; and 18% had four or more televisions. Create a histogram for these percentages. (Treat “four or more televisions” as four for the purposes of this exercise.)

Question 2.36

2.36

Skew and surname frequencies: Researchers published a summary of the frequency of surnames based on U.S. Census data (Word, Coleman, Nunziata, & Kominski, 2008). The table lists the frequencies of last names in the left column, the number of last names with that level of frequency in the next column, and then the cumulative number and cumulative proportion (or percentage) in the next two columns. For example, 2.3 million people in the United States have the last name Smith, the most common name in this data set. So, Smith would be one of the seven names listed in the top row—last names that occur more than 1,000,000 times in the population. In another example, more than 72,000 people have the last name Singh. So, Singh is one of the 3012 surnames in the third row—names that occur between 10,000 and 99,999 times in the population.

43

  1. Is this a frequency table or a grouped frequency table? Explain your answer.

  2. How is this table different from the tables you created in this chapter? Why do you think the researchers constructed this table differently?

  3. Based on this table, does this distribution seem to be normal, negatively skewed, or positively skewed? Explain your answer.

  4. Is there a floor effect or a ceiling effect? Explain your answer.

Last Names
Frequency of Occurrence Number Cumulative Number Cumulative Proportion (percent)
1,000,000+ 7 7 0.0
100,000–999,999 268 275 0.0
10,000–99,999 3012 3287 0.1
1000–9999 20,369 23,656 0.4
100–999 128,015 151,671 2.4
50–99 105,609 257,280 4.1
25–49 166,059 423,339 6.8
10–24 331,518 754,857 12.1
5–9 395,600 1,150,457 18.4
2–4 1,056,992 2,207,449 35.3
1 4,040,966 6,248,415 100.0

Question 2.37

2.37

Skew and movie ratings: IMDb (Internet Movie Database) publishes average ratings of movies worldwide. Anyone can log on and rate a film. What’s the worst-rated film of the more than 235,000 that are listed on IMDb? The Bollywood action-romance Gunday, which earned a rating of 1.4 on a scale of 1–10 (Goldenburg, 2014). Hardly any other movies even came close to that low rating. In fact, the average film is rated 6.3, and most of the movies garnered ratings between 5.5 and 7.2. Even though Gunday got pretty good critical reviews, including three out of four stars from Roger Ebert, it tanked on the crowd-sourced IMDb. Why? Activists in Bangladesh harnessed social media to give it a bad rating. One posted “If you’re a Bangladeshi and care enough to not let some Indian crappy movie distort our history of independence, let’s unite and boycott this movie!!!”

  1. Based on what you know about the typical ratings on IMDb, is a frequency polygon based on these data likely to be normally distributed, negatively skewed, or positively skewed? Explain your answer.

  2. Is there more likely to be a floor effect or a ceiling effect for these data? Explain your answer.

  3. Based on this story, are audience-generated IMDb ratings a good way to operationalize the quality of a movie? What might be a better way?

Putting It All Together

Question 2.38

2.38

Frequencies, distributions, and numbers of friends: A college student is interested in how many friends the average person has. She decides to count the number of people who appear in photographs on display in dorm rooms and offices across campus. She collects data on 84 students and 33 faculty members. The data are presented below.
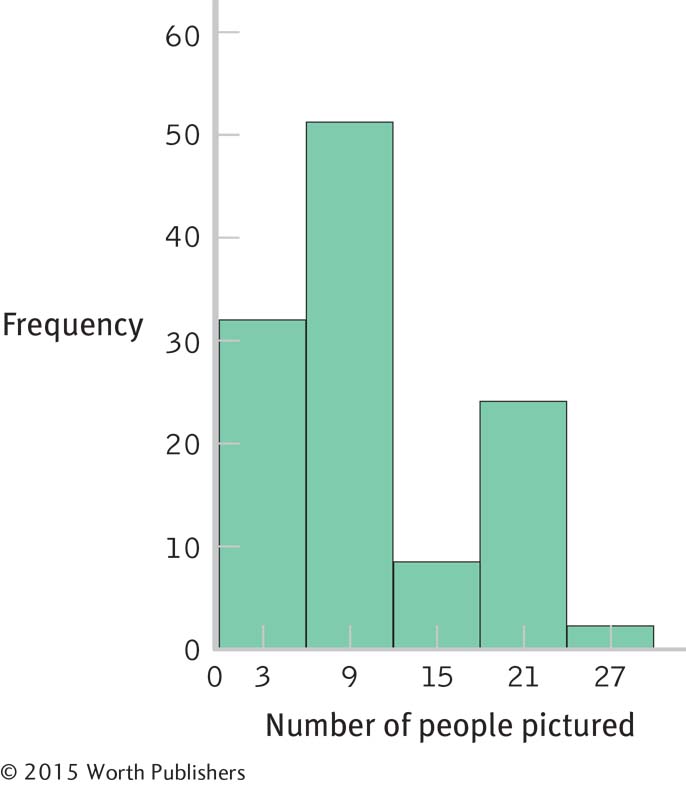
image

  1. What kind of visual display is this?

  2. Estimate how many people have fewer than 6 people pictured.

  3. Estimate how many people have more than 18 people pictured.

  4. Can you think of additional questions you might ask after reviewing the data displayed here?

  5. Below is a subset of the data described here. Create a grouped frequency table for these data, using seven groupings.

    1 5 3 9 13 0 18 15
    3 3 5 7 7 7 11 3
    12 20 16 4 17 15 16 10
    6 8 8 7 3 17

    44

  6. Create a histogram of the grouped data from (e).

  7. Describe how the data depicted in the original graph and the histogram you created in part (f) are distributed.

Question 2.39

2.39

Frequencies, distributions, and breast-feeding duration: The Centers for Disease Control and other organizations are interested in the health benefits of breast-feeding for infants. The National Immunization Survey includes questions about breast-feeding practices, including: “How long was [your child] breast-fed or fed breast milk?” The data for duration of breast-feeding, in months, for 20 hypothetical mothers are presented below.
0 7 0 12 9 3 2 0 6 10
3 0 2 1 3 0 3 1 1 4

  1. Create a frequency table for these data. Include a third column for percentages.

  2. Create a histogram of these data.

  3. Create a frequency polygon of these data.

  4. Create a grouped frequency table for these data with three groups (create groupings around the midpoints of 2.5 months, 7.5 months, and 12.5 months).

  5. Create a histogram of the grouped data.

  6. Create a frequency polygon of the grouped data.

  7. Write a summary describing the distribution of these data with respect to shape and direction of any skew.

  8. If you wanted the data to be normally distributed around 12 months, how would the data have to shift to fit that goal? How could you use knowledge about the current distribution to target certain women?

Question 2.40

2.40

Developing research ideas from frequency distributions: Below are frequency distributions for two sets of the friends data described in Exercise 2.38, one for the students and one for the faculty members studied.
Interval Faculty Frequency Student Frequency
0–3 21 0
4–7 11 26
8–11 1 24
12–15 0 2
16–19 0 27
20–23 0 37
24–27 0 2

  1. How would you describe the distribution for faculty members?

  2. How would you describe the distribution for students?

  3. If you were to conduct a study comparing the numbers of friends that faculty members and students have, what would the independent variable be and what would be the levels of the independent variable?

  4. In the study described in (c), what would the dependent variable be?

  5. What is a confounding variable that might be present in the study described in (c)?

  6. Suggest at least two additional ways to operationalize the dependent variable. Would either of these ways reduce the impact of the confounding variable described in (e)?

Question 2.41

2.41

Frequencies, distributions, and graduate advising: In a study of mentoring in chemistry fields, a team of chemists and social scientists identified the most successful U.S. mentors—professors whose students were hired by the top 50 chemistry departments in the United States (Kuck et al., 2007). Fifty-four professors had at least three students go on to such jobs. Here are the data for the 54 professors. Each number indicates the number of students successfully mentored by each different professor.
3 3 3 4 5 9 5 3 3 5 6
3 4 8 6 3 3 3 4 4 4 7
6 3 5 5 7 13 3 3 3 3 3
4 4 4 5 6 7 6 7 8 8 3
3 3 5 3 3 5 3 5 3 3

  1. Construct a frequency table for these data. Include a third column for percentages.

  2. Construct a histogram for these data.

  3. Construct a frequency polygon for these data.

  4. Describe the shape of this distribution.

  5. How did the researchers operationalize the variable of mentoring success? Suggest at least two other ways in which they might have operationalized mentoring success.

  6. Imagine that researchers hypothesized that an independent variable—the number of publications coauthored by the advisor—predicts the dependent variable of mentoring success. One professor, (Dr. Yuan T. Lee), from the University of California at Berkeley, trained 13 future top faculty members. (Dr. Lee) won a Nobel Prize. Explain how such a prestigious and public accomplishment might present a confounding variable to the hypothesis described above.

    45

  7. Dr. Lee had many students who went on to top professorships before he won his Nobel Prize. Several other chemistry Nobel Prize winners in the United States serve as graduate advisors but have not had Dr. Lee’s level of success as mentors. What are other possible variables that might predict the dependent variable of attaining a top professor position?