Chapter 10 How it Works

10.1 CONDUCTING A PAIRED-SAMPLES t Test

Salary Wizard is an online tool that allows you to look up incomes for specific jobs for cities in the United States. We looked up the 25th percentile for income for six jobs in two cities: Boise, Idaho, and Los Angeles, California. The data are below.

Boise Los Angeles
Executive chef $53,047.00 $62,490.00
Genetics counselor $49,958.00 $58,850.00
Grants/proposal writer $41,974.00 $49,445.00
Librarian $44,366.00 $52,263.00
Public schoolteacher $40,470.00 $47,674.00
Social worker (with bachelor’s degree) $36,963.00 $43,542.00

How can we conduct a paired-samples t test to determine whether income in one of these cities differs, on average, from income in the other? We’ll use a two-tailed test and a p level of 0.05.

  1. Population 1: Job types in Boise, Idaho. Population 2: Job types in Los Angeles, California.

    The comparison distribution will be a distribution of mean differences. The hypothesis test will be a paired-samples t test because we have two samples, and all participants—the job types, in this case—are in both samples.

    This study meets the first of the three assumptions and may meet the third. The dependent variable, income, is scale. We do not know whether the population is normally distributed, there are not at least 30 participants, and there is not much variability in the data in the samples, so we should proceed with caution. The data were not randomly selected, so we should be cautious when generalizing beyond this sample of job types.

  2. Null hypothesis: Jobs in Boise pay the same, on average, as jobs in Los Angeles—H0: μ1 = μ2. Research hypothesis: Jobs in Boise pay different incomes, on average, than do jobs in Los Angeles—H1: μ1 ≠ μ2.
  3. μM = μ = 0; sM = 438.919
    Boise Los Angeles Difference (D) (D − Mdifference) (D − Mdifference)2
    $53,047.00 $62,490.00 9443 1528.667 2,336,822.797
    $49,958.00 $58,850.00 8892 977.667 955,832.763
    $41,974.00 $49,445.00 7471 − 443.333 196,544.149
    $44,366.00 $52,263.00 7897 −17.333 300.433
    $40,470.00 $47,674.00 7204 −710.333 504,572.971
    $36,963.00 $43,542.00 6579 −1335.333 1,783,114.221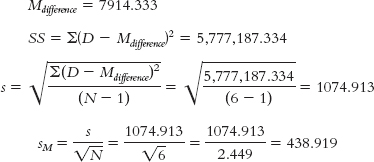

  4. df = N − 1 = 6 − 1 = 5

    The critical values, based on 5 degrees of freedom, a p level of 0.05, and a two-tailed test, are −2.571 and 2.571.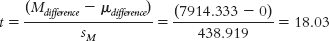

  5. 257

  6. Reject the null hypothesis. It appears that jobs in Los Angeles pay more, on average, than do jobs in Boise.

    The statistics, as they would be presented in a journal article, are:

    t(5) = 18.03, p < 0.05