Chapter 11 Exercises
Clarifying the Concepts
Question 11.1
When is it appropriate to use the independent-
Question 11.2
Explain random assignment and what it controls.
Question 11.3
What are independent events?
Question 11.4
Explain how the paired-
Question 11.5
As they relate to comparison distributions, what is the difference between mean differences and differences between means?
Question 11.6
As measures of variability, what is the difference between standard deviation and variance?
Question 11.7
What is the difference between 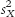
and 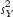
?
Question 11.8
What is pooled variance?
Question 11.9
Why would we want the variability estimate based on a larger sample to count more (to be more heavily weighted) than one based on a smaller sample?
Question 11.10
Define the symbols in the following formula: 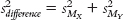
Question 11.11
How do confidence intervals relate to margin of error?
Question 11.12
What is the difference between pooled variance and pooled standard deviation?
Question 11.13
How does the size of the confidence interval relate to the precision of the prediction?
Question 11.14
Why does the effect-
Question 11.15
Explain how we determine standard deviation (needed to calculate Cohen’s d) from the several steps of calculations we made to determine standard error.
Question 11.16
For an independent-
Question 11.17
How do we interpret effect size using Cohen’s d?
Question 11.18
Why might we want to transform data?
282
Question 11.19
What does the square root transformation do to the distribution of data?
Calculating the Statistic
Question 11.20
Below are several sample means. For each class, calculate the differences between the means for students who sit in the front versus the back of a classroom.
| Mean test grades | Students in the front | Students in the back |
|---|---|---|
| Class 1 | 82 | 78 |
| Class 2 | 79.5 | 77.41 |
| Class 3 | 71.5 | 76 |
| Class 4 | 72 | 71.3 |
Question 11.21
Consider the following data from two independent groups:
Group 1: 97, 83, 105, 102, 92
Group 2: 111, 103, 96, 106
Calculate s2 for group 1 and for group 2.
Calculate dfX, dfY, and dftotal.
Determine the critical values for t, assuming a two-
tailed test with a p level of 0.05. Calculate pooled variance,
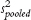
.Calculate the variance version of standard error for each group.
Calculate the variance and the standard deviation of the distribution of differences between means.
Calculate the t statistic.
Calculate the 95% confidence interval.
Calculate Cohen’s d.
Question 11.22
Consider the following data from two independent groups:
Liberals: 2, 1, 3, 2
Conservatives: 4, 3, 3, 5, 2, 4
Calculate s2 for each group.
Calculate dfX, dfY, and dftotal.
Determine the critical values for t, assuming a two-
tailed test with a p level of 0.05. Calculate pooled variance,
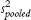
.Calculate the variance version of standard error for each group.
Calculate the variance and the standard deviation of the distribution of differences between means.
Calculate the t statistic.
Calculate the 95% confidence interval.
Calculate Cohen’s d.
Question 11.23
Find the critical t values for the following data sets:
Group 1 has 21 participants and group 2 has 16 participants. You are performing a two-
tailed test with a p level of 0.05. You studied 3-
year- old children and 6- year- old children, with samples of 12 and 16, respectively. You are performing a two- tailed test with a p level of 0.01. You have a total of 17 degrees of freedom for a two-
tailed test and a p level of 0.10.
Question 11.24
Use the following data set to answer the questions below:
15 24 35 16 18 22 16 72
Calculate the mean and median of the data set. What do the mean and median suggest about the distribution of the data?
Apply the square root transformation to the data set.
Calculate the mean and median for the transformed data. How has the relation between the mean and median changed? What does this suggest about the distribution of the transformed data?
Question 11.25
For each of the following sets of data, indicate whether you would apply a square root transformation to the data and explain why you would or wouldn’t.
10 15 18 20 22 25 30 17 23
23 10 67 2 56 34 47 5 26 13
32 88 75 71 89 91 94 75 87 78
Applying the Concepts
Question 11.26
Making a decision: Numeric results for several independent-
A total of 73 people were studied, 40 in one group and 33 in the other group. The test statistic was calculated as 2.13 for a two-
tailed test with a p level of 0.05. One group of 23 people was compared to another group of 18 people. The t statistic obtained for their data was 1.77. Assume you were performing a two-
tailed test with a p level of 0.05. One group of nine mice was compared to another group of six mice, using a two-
tailed test at a p level of 0.01. The test statistic was calculated as 3.02.
Question 11.27
The independent-
283
Sample 1: 12.6, 13.8, 11.6, 12.2, 12.1, 13.0
Sample 2: 8.5, 9.6, 10.0, 9.2, 8.9, 10.8
Conduct all six steps of an independent-
samples t test. Be sure to label all six steps. Report the statistics as you would in a journal article.
What happens to the test statistic when you switch from having all participants be in both samples to having two separate samples? Given the same numbers, is it easier to reject the null hypothesis with a within-
groups design or with a between- groups design? In your own words, why do you think it is easier to reject the null hypothesis in one of these situations than in the other?
Calculate the 95% confidence interval.
State in your own words what we learn from this confidence interval.
What information does the confidence interval give us that we also get from the hypothesis test?
What additional information does the confidence interval give us that we do not get from the hypothesis test?
Calculate the appropriate measure of effect size.
Based on Cohen’s conventions, is this a small, medium, or large effect size?
Why is it useful to have this information in addition to the results of a hypothesis test?
Question 11.28
An independent-
Men: 28, 35, 52, 14
Women: 30, 82, 53, 61
Conduct all six steps of an independent-
samples t test. Be sure to label all six steps. Report the statistics as you would in a journal article.
Calculate the 95% confidence interval.
Calculate the 90% confidence interval.
How are the confidence intervals different from each other? Explain why they are different.
Calculate the appropriate measure of effect size.
Based on Cohen’s conventions, is this a small, medium, or large effect size?
Why is it useful to have this information in addition to the results of a hypothesis test?
Question 11.29
An independent-
Men: 16,345 17,222 15,646 14,889 16,701
Women: 17,345 15,593 16,624 16,696 14,200
Conduct all six steps of an independent-
samples t test. Be sure to label all six steps. Report the statistics as you would in a journal article.
Calculate the 95% confidence interval.
Express the confidence interval in writing, according to the format discussed in the chapter.
State in your own words what we learn from this confidence interval.
Calculate the appropriate measure of effect size.
Based on Cohen’s conventions, is this a small, medium, or large effect size?
Why is it useful to have this information in addition to the results of a hypothesis test?
Question 11.30
An independent-
284
All-
Noninclusive resort guests: 3, 15, 7
Conduct all six steps of an independent-
samples t test. Be sure to label all six steps. Report the statistics as you would in a journal article.
Is there a shortcut you could or did use to compute your hypothesis test? (Hint: There are equal numbers of participants in the two groups.)
Calculate the 95% confidence interval.
State in your own words what we learn from this confidence interval.
Express the confidence interval, in a sentence, as a margin of error.
Calculate the appropriate measure of effect size.
Based on Cohen’s conventions, is this a small, medium, or large effect size?
Why is it useful to have this information in addition to the results of a hypothesis test?
Question 11.31
An independent-
Mothers: 33, 55, 39, 41, 67
Nonmothers: 56, 48, 71
Conduct all six steps of an independent-
samples t test. Be sure to label all six steps. Report the statistics as you would in a journal article.
Calculate the 95% confidence interval.
State in your own words what we learn from this confidence interval.
Explain why interval estimates are better than point estimates.
Calculate the appropriate measure of effect size.
Based on Cohen’s conventions, is this a small, medium, or large effect size?
Why is it useful to have this information in addition to the results of a hypothesis test?
Question 11.32
Choosing a hypothesis test: For each of the following three scenarios, state which hypothesis test you would use from among the four introduced so far: the z test, the single-
A study of 40 children who had survived a brain tumor revealed that they were more likely to have behavioral and emotional difficulties than were children who had not experienced such a trauma (Upton & Eiser, 2006). Parents rated children’s difficulties, and the ratings data were compared with known means from published population norms.
Talarico and Rubin (2003) recorded the memories of 54 students just after the terrorist attacks in the United States on September 11, 2001—
some memories related to the terrorist attacks on that day (called flashbulb memories for their vividness and emotional content) and some everyday memories. They found that flashbulb memories were no more consistent over time than everyday memories, even though they were perceived to be more accurate. The HOPE VI Panel Study (Popkin & Woodley, 2002) was initiated to test a U.S. program aimed at improving troubled public housing developments. Residents of five HOPE VI developments were examined at the beginning of the study so researchers could later ascertain whether their quality of life had improved. Means at the beginning of the study were compared to known national data sources (e.g., the U.S. Census, the American Housing Survey) that had summary statistics, including means and standard deviations.
Question 11.33
Choosing a hypothesis test: For each of the following three scenarios, state which hypothesis test you would use from among the four introduced so far: the z test, the single-
Taylor and Ste-
Marie (2001) studied eating disorders in 41 Canadian female figure skaters. They compared the figure skaters’ data on the Eating Disorder Inventory to the means of known populations, including women with eating disorders. On average, the figure skaters were more similar to the population of women with eating disorders than to those without eating disorders. In an article titled “A Fair and Balanced Look at the News: What Affects Memory for Controversial Arguments,” Wiley (2005) found that people with a high level of previous knowledge about a given controversial topic (e.g., abortion, military intervention) had better average recall for arguments on both sides of that issue than did those with lower levels of knowledge.
Engle-
Friedman and colleagues (2003) studied the effects of sleep deprivation. Fifty students were assigned to one night of sleep loss (students were required to call the laboratory every half- hour all night) and then one night of no sleep loss (normal sleep). The next day, students were offered a choice of math problems with differing levels of difficulty. Following sleep loss, students tended to choose less challenging problems.
Question 11.34
Null and research hypotheses: Using the research studies described here (from Exercise 11.33), create null hypotheses and research hypotheses appropriate for the chosen statistical test:
Taylor and Ste-
Marie (2001) studied eating disorders in 41 Canadian female figure skaters. They compared the figure skaters’ data on the Eating Disorder Inventory to the means of known populations, including women with eating disorders. On average, the figure skaters were more similar to the population of women with eating disorders than to those without eating disorders. In article titled “A Fair and Balanced Look at the News: What Affects Memory for Controversial Arguments,” Wiley (2005) found that people with a high level of previous knowledge about a given controversial topic (e.g., abortion, military intervention) had better average recall for arguments on both sides of that issue than did those with lower levels of knowledge.
Engle-
Friedman and colleagues (2003) studied the effects of sleep deprivation. Fifty students were assigned to one night of sleep loss (students were required to call the laboratory every half- hour all night) and then one night of no sleep loss (normal sleep). The next day, students were offered a choice of math problems with differing levels of difficulty. Following sleep loss, students tended to choose less challenging problems.
Question 11.35
Independent-
Why would an independent-
samples t test be appropriate in this situation? What would the null hypothesis and research hypothesis be in this situation?
Question 11.36
Independent-
A “Speed Camera Lottery”—in which an electronic sign told people how fast they were going so they could adjust their speed—
was introduced. As people passed the electronic sign, a camera took a photo of their license plate. If they were speeding, they were mailed a ticket and had to pay a fine. If they were obeying the speed limit, they were entered into a lottery to win some of the money from those who paid speeding tickets. The average speed using the Speed Camera Lottery sign was 25 kilometers per hour, and the average speed with no lottery sign was 32 kilometers per hour. At the exit of a subway station, stairs and an escalator were side by side. The stairs were turned into a piano, so that when you climbed them, you heard musical notes. While the Piano Staircase was in place, 66% more people took the stairs—
rather than the escalator— than when the Piano Staircase was not in place. A trash bin was designed so that when someone threw trash into it, there was a long whistling sound, followed by a thud, as if the trash were falling into an extremely deep bin. When the bin was used, an average of 72 kg of trash was disposed of in a day; when it was not used, an average of 31 kg of trash was disposed of in a day.
Question 11.37
Cafeteria trays, food consumption, and an independent-
What was the independent variable and what were its levels?
What were the dependent variables? How did the researchers likely operationalize their variables?
The researchers describe their study as an experiment. Explain what they mean by this.
Why would it be possible to use independent-
samples t tests to analyze the data from their study? The researchers also report: “Prior to the analysis, the data were transformed.” Explain why they may have decided to transform the data.
286
Putting It All Together
Question 11.38
Gender and number words: Chang, Sandhofer, and Brown (2011) wondered whether mothers used number words more with their preschool sons than with their preschool daughters. Each participating family included one mother and one child—
Is this a between-
groups or within- groups design? Explain your answer. What is the independent variable? What is the dependent variable?
How many children were in the total sample? Explain how you determined this.
Is the sample likely randomly selected? Is it likely that the researchers used random assignment?
Were the researchers able to reject the null hypothesis? Explain.
What can you say about the size of the effect?
Describe how you could design an experiment to test whether exposure to more number words in preschool leads children to like mathematics more when they enter school.
Question 11.39
School lunches: Alice Waters, owner of the Berkeley, California, restaurant Chez Panisse, has long been an advocate for the use of simple, fresh, organic ingredients in home and restaurant cooking. She has also turned her considerable expertise to school cafeterias. Waters (2006) praised changes in school lunch menus that have expanded nutritious offerings, but she hypothesizes that students are likely to circumvent healthy lunches by avoiding vegetables and smuggling in banned junk food unless they receive accompanying nutrition education and hands-
In your own words, what is Waters predicting? Citing the confirmation bias, explain why Waters’ program, although intuitively appealing, should not be instituted nationwide without further study.
Describe a simple between-
groups experiment with a nominal independent variable with two levels and a scale- dependent variable to test Waters’ hypothesis. Specifically identify the independent variable, its levels, and the dependent variable. State how you will operationalize the dependent variable. Which hypothesis test would be used to analyze this experiment? Explain your answer.
Conduct step 1 of hypothesis testing.
Conduct step 2 of hypothesis testing.
State at least one other way you could operationalize the dependent variable.
Let’s say, hypothetically, that Waters discounted the need for the research you propose by citing her own data that the Berkeley school in which she instituted the program has lower rates of obesity than other California schools. Describe the flaw in this argument by discussing the importance of random selection and random assignment.
Question 11.40
Perception and portion sizes: Researchers at the Cornell University Food and Brand Lab conducted an experiment at a fitness camp for adolescents (Wansink & van Ittersum, 2003). Campers were given either a 22-
Is it likely that the researchers used random selection? Explain.
Is it likely that the researchers used random assignment? Explain.
What is the independent variable, and what are its levels?
What is the dependent variable?
What hypothesis test would the researchers use? Explain.
Conduct step 1 of hypothesis testing.
Conduct step 2 of hypothesis testing.
How could the researchers redesign this study so that they could use a paired-
samples t test?