12.2 One-Way Between-Groups ANOVA
The self-
Everything About ANOVA but the Calculations
To introduce the steps of hypothesis testing for a one-
EXAMPLE 12.1
The researchers studied people in 15 societies from around the world. For teaching purposes, we’ll look at data from four types of societies—
- Foraging. Several societies, including ones in Bolivia and Papua New Guinea, were categorized as foraging societies. They acquired most of their food through hunting and gathering.
- Farming. Some societies, including ones in Kenya and Tanzania, primarily practiced farming and tended to grow their own food.
- Natural resources. Other societies, such as in Colombia, built their economies by extracting natural resources, such as trees and fish. Most food was purchased.
- Industrial. In industrial societies, which include the major city of Accra in Ghana as well as rural Missouri in the United States, most food was purchased.
The researchers wondered which groups would behave more or less fairly toward others—

This research design would be analyzed with a one-
296
- Foraging: 28, 36, 38, 31
- Farming: 32, 33, 40
- Natural resources: 47, 43, 52
- Industrial: 40, 47, 45
Let’s begin by applying a familiar framework: the six steps of hypothesis testing. We will learn the calculations in the next section.
STEP 1: Identify the populations, distribution, and assumptions.
The first step of hypothesis testing is to identify the populations to be compared, the comparison distribution, the appropriate test, and the assumptions of the test. Let’s summarize the fairness study with respect to this first step of hypothesis testing.
Summary: The populations to be compared: Population 1: All people living in foraging societies. Population 2: All people living in farming societies. Population 3: All people living in societies that extract natural resources. Population 4: All people living in industrial societies.
The comparison distribution and hypothesis test: The comparison distribution will be an F distribution. The hypothesis test will be a one-
Assumptions: (1) The data are not selected randomly, so we must generalize only with caution. (2) We do not know if the underlying population distributions are normal, but the sample data do not indicate severe skew. (3) We will test homoscedasticity when we calculate the test statistics by checking whether the largest variance is not more than twice the smallest. (Note: Don’t forget this step just because it comes later in the analysis.)
STEP 2: State the null and research hypotheses.
The second step is to state the null and research hypotheses. As usual, the null hypothesis posits no difference among the population means. The symbols are the same as before, but with more populations: H0: μ1 = μ2 = μ3 = μ4. However, the research hypothesis is more complicated because we can reject the null hypothesis if only one group is different, on average, from the others. The research hypothesis that μ1 ≠ μ2 ≠ μ3 ≠ μ4 does not include all possible outcomes, such as the hypothesis that the mean fairness scores for groups 1 and 2 are greater than the mean fairness scores for groups 3 and 4. The research hypothesis is that at least one population mean is different from at least one other population mean, so H1 is that at least one μ is different from another μ.
Summary: Null hypothesis: People living in societies based on foraging, farming, the extraction of natural resources, and industry all exhibit, on average, the same fairness behaviors—
297
STEP 3: Determine the characteristics of the comparison distribution.
The third step is to explicitly state the relevant characteristics of the comparison distribution. This step is an easy one in ANOVA because most calculations are in step 5. Here we merely state that the comparison distribution is an F distribution and provide the appropriate degrees of freedom. As we discussed, the F statistic is a ratio of two independent estimates of the population variance, between-
MASTERING THE FORMULA
12-
dfbetween = Ngroups − 1 = 4 − 1 = 3
Because there are four groups (foraging, farming, the extraction of natural resources, and industry), the between-
The sample within-
df1 = n1 − 1 = 4 − 1 = 3
n represents the number of participants in the particular sample. We would then do this for the remaining samples. For this example, there are four samples, so the formula would be:
MASTERING THE FORMULA
12-
dfwithin = df1 + df2 + df3 + df4
For this example, the calculations would be:
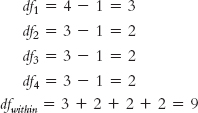
Summary: We would use the F distribution with 3 and 9 degrees of freedom.
STEP 4: Determine the critical value, or cutoff.
The fourth step is to determine a critical value, or cutoff, indicating how extreme the data must be to reject the null hypothesis. For ANOVA, we use an F statistic, for which the critical value on an F distribution will always be positive (because the F is based on estimates of variance and variances are always positive). We determine the critical value by examining the F table in Appendix B (excerpted in Table 12-3). The between-
298

Use the F table by first finding the appropriate within-
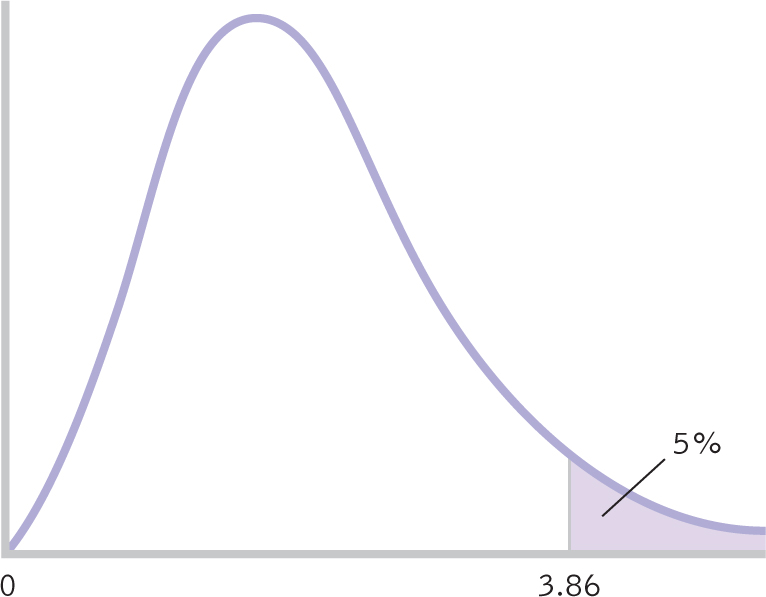
Figure 12-
Summary: The cutoff, or critical value, for the F statistic for a p level of 0.05 is 3.86, as displayed in the curve in Figure 12-2.
STEP 5: Calculate the test statistic.
In the fifth step, we calculate the test statistic. We use the two estimates of the between-
Summary: To be calculated in the next section.
299
STEP 6: Make a decision.
In the final step, we decide whether to reject or fail to reject the null hypothesis. If the F statistic is beyond the critical value, then we know that it is in the most extreme 5% of possible test statistics if the null hypothesis is true. We can then reject the null hypothesis and conclude, “It seems that people exhibit different fairness behaviors, on average, depending on the type of society in which they live.” ANOVA only tells us that at least one mean is significantly different from another; it does not tell us which societies are different.
MASTERING THE CONCEPT
12.2: When conducting an ANOVA, we use the same six steps of hypothesis testing that we’ve already learned. One of the differences from what we’ve learned is that we calculate an F statistic, the ratio of between-
If the test statistic is not beyond the critical value, then we must fail to reject the null hypothesis. The test statistic would not be very rare if the null hypothesis were true. In this circumstance, we report only that there is no evidence from the present study to support the research hypothesis.
Summary: Because the decision we will make must be evidence based, we cannot make it until we complete step 5, in which we calculate the probabilities associated with that evidence. We will complete step 6 in the Making a Decision section.
The Logic and Calculations of the F Statistic

In this section, we first review the logic behind ANOVA’s use of between-
As we noted before, grown men, on average, are slightly taller than grown women, on average. We call that “between-
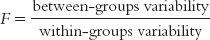
Quantifying Overlap with ANOVA
Many women are taller than many men, so their distributions overlap. The amount of overlap is influenced by the distance between the means (between-
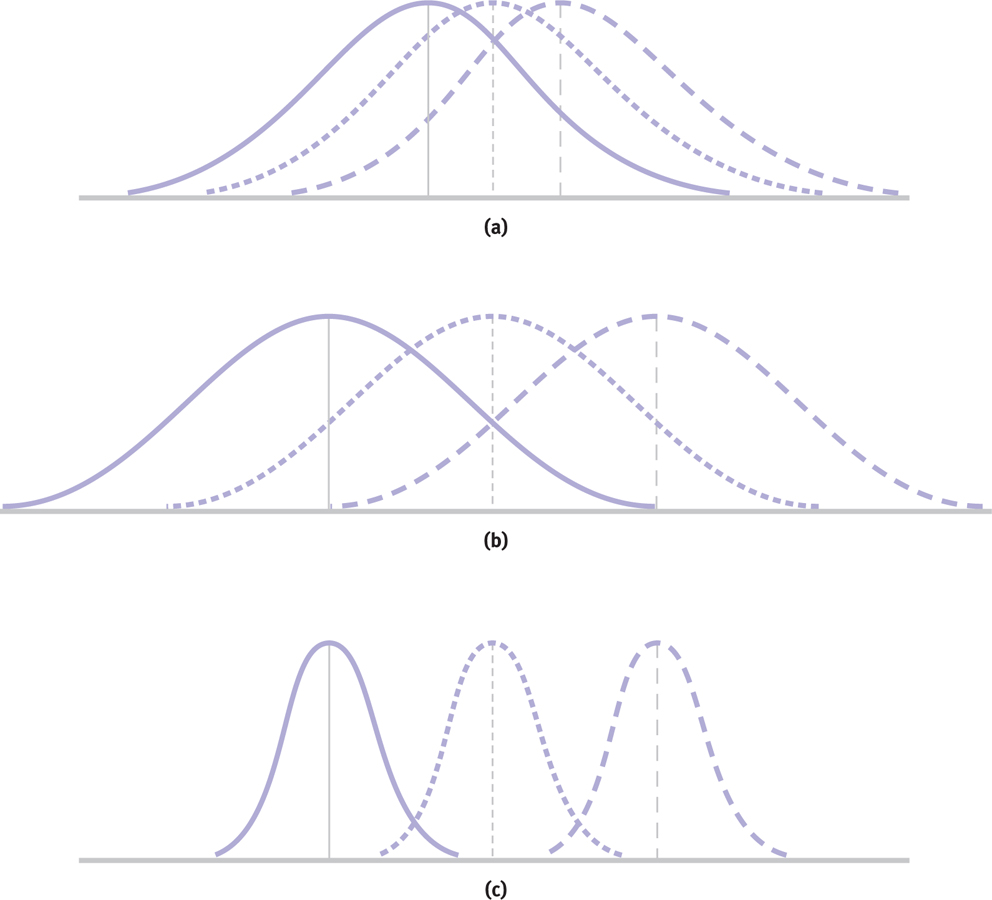
Figure 12-
There is less overlap in the second set of distributions (b), but only because the means are farther apart; the within-
300
There is even less overlap in the third set of distributions (c) because the numerator representing the between-
Two Ways to Estimate Population Variance
Between-
Calculating the F Statistic with the Source Table
A source table presents the important calculations and final results of an ANOVA in a consistent and easy-
The goal of any statistical analysis is to understand the sources of variability in a study. We achieve that in ANOVA by calculating many squared deviations from the mean and three sums of squares. We organize the results into a source table that presents the important calculations and final results of an ANOVA in a consistent and easy-
301
| 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| Source | SS | df | MS | F |
| Between | SSbetween | dfbetween | MSbetween | F |
| Within | SSwithin | dfwithin | MSwithin | |
| Total | SStotal | dftotal |
Column 1: “Source.” One possible source of population variance comes from the spread between means; a second source comes from the spread within each sample. In this chapter, the row labeled “Total” allows us to check the calculations of the sum of squares (SS) and degrees of freedom (df). Now let’s work backward through the source table to learn how it describes these two familiar sources of variability.
Column 5: “F.” We calculate F using simple division: between-
Column 4: “MS.” MS is the conventional symbol for variance in ANOVA. It stands for “mean square” because variance is the arithmetic mean of the squared deviations for between-
Column 3: “df.” We calculate the between-
dftotal = dfbetween + dfwithin
In our version of the fairness study, dftotal = 3 + 9 = 12. A second way to calculate dftotal is:
dftotal = Ntotal − 1
Ntotal refers to the total number of people in the entire study. In our abbreviated version of the fairness study, there were four groups, with 4, 3, 3, and 3 participants in the groups, and 4 + 3 + 3 + 3 = 13. We calculate total degrees of freedom for this study as dftotal = 13 − 1 = 12. If we calculate degrees of freedom both ways and the answers don’t match up, then we know we have to go back and check the calculations.
Column 2: “SS.” We calculate three sums of squares. One SS represents between-
MASTERING THE FORMULA
12-
302
The source table is a convenient summary because it describes everything we have learned about the sources of numerical variability. Once we calculate the sums of squares for between-
Step 1: Divide each sum of squares by the appropriate degrees of freedom—
Step 2: Calculate the ratio of MSbetween and MSwithin to get the F statistic. Once we have the sums of squared deviations, the rest of the calculation is simple division.
Sums of Squared Deviations
Language Alert! The term “deviations” is another word used to describe variability. ANOVA analyzes three different types of statistical deviations: (1) deviations between groups, (2) deviations within groups, and (3) total deviations. We begin by calculating the sum of squares for each type of deviation, or source of variability: between, within, and total.
It is easiest to start with the total sum of squares, SStotal. Organize all the scores and place them in a single column with a horizontal line dividing each sample from the next. Use the data (from our version of the fairness study) in the column labeled “X” of Table 12-5 as your model; X stands for each of the 13 individual scores listed below. Each set of scores is next to its sample; the means are underneath the names of each respective sample. (We have included subscripts on each mean in the first column—
| Sample | X | (X − GM) | (X − GM)2 |
|---|---|---|---|
| Foraging | 28 | −11.385 | 129.618 |
| 36 | −3.385 | 11.458 | |
| 38 | −1.385 | 1.918 | |
| Mfor = 33.250 | 31 | −8.385 | 70.308 |
| Farming | 32 | −7.385 | 54.538 |
| 33 | −6.385 | 40.768 | |
| Mfarm = 35.000 | 40 | 0.615 | 0.378 |
| Natural resources | 47 | 7.615 | 57.988 |
| 43 | 3.615 | 13.068 | |
| Mnr = 47.333 | 52 | 12.615 | 159.138 |
| Industrial | 40 | 0.615 | 0.378 |
| 47 | 7.615 | 57.988 | |
| Mind = 44.000 | 45 | 5.615 | 31.528 |
| GM = 39.385 | SStotal = 629.074 |
The grand mean is the mean of every score in a study, regardless of which sample the score came from.
To calculate the total sum of squares, subtract the overall mean from each score, including everyone in the study, regardless of sample. The mean of all the scores is called the grand mean, and its symbol is GM. The grand mean is the mean of every score in a study, regardless of which sample the score came from:
MASTERING THE FORMULA
12-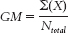 . We add up everyone’s score, then divide by the total number of people in the study.
. We add up everyone’s score, then divide by the total number of people in the study.

303
The grand mean of these scores is 39.385. (As usual, we write each number to three decimal places until we get to the final answer, F. We report the final answer to two decimal places.)
The third column in Table 12-5 shows the deviation of each score from the grand mean. The fourth column shows the squares of these deviations. For example, for the first score, 28, we subtract the grand mean:
28 − 39.385 = −11.385
| Sample | X | (X − M) | (X − M)2 |
|---|---|---|---|
| Foraging | 28 | −5.25 | 27.563 |
| 36 | 2.75 | 7.563 | |
| Mfor = 33.250 | 38 | 4.75 | 22.563 |
| 31 | −2.25 | 5.063 | |
| Farming | 32 | −3.000 | 9.000 |
| 33 | −2.000 | 4.000 | |
| Mfarm = 35.000 | 40 | 5.000 | 25.000 |
| Natural resources | 47 | −0.333 | 0.111 |
| 43 | −4.333 | 18.775 | |
| Mnr = 47.333 | 52 | 4.667 | 21.781 |
| Industrial | 40 | −4.000 | 16.000 |
| 47 | 3.000 | 9.000 | |
| Mind = 44.000 | 45 | 1.000 | 1.000 |
| GM = 39.385 | SSwithin = 167.419 |
Then we square the deviation:
(−11.385)2 = 129.618
Below the fourth column, we have summed the squared deviations: 629.074. This is the total sum of squares, SStotal. The formula for the total sum of squares is:
MASTERING THE FORMULA
12-
SStotal = Σ(X − GM)2
The model for calculating the within-
(28 − 33.25)2 = 27.563
For the three scores in the second sample, we subtract their sample mean, 35.0. And so on for all four samples. (Note: Don’t forget to switch means when you get to each new sample!)
304
Once we have all the deviations, we square them and sum them to calculate the within-
MASTERING THE FORMULA
12-
SSwithin = Σ(X − M)2
Notice how the weighting for sample size is built into the calculation: The first sample has four scores and contributes four squared deviations to the total. The other samples have only three scores, so they only contribute three squared deviations.
Finally, we calculate the between-
For example, the first person has a score of 28 and belongs to the group labeled “foraging,” which has a mean score of 33.25. The grand mean is 39.385. We ignore this person’s individual score and subtract 39.385 (the grand mean) from 33.25 (the group mean) to get the deviation score, −6.135. The next person, also in the group labeled “foraging,” has a score of 36. The group mean of that sample is 33.25. Once again, we ignore that person’s individual score and subtract 39.385 (the grand mean) from 33.25 (the group mean) to get the deviation score, also −6.135.
In fact, we subtract 39.385 from 33.25 for all four scores, as you can see in Table 12-7. When we get to the horizontal line between samples, we look for the next sample mean. For all three scores in the next sample, we subtract the grand mean, 39.385, from the sample mean, 35.0, and so on.
| Sample | X | (M − GM) | (M − GM)2 |
|---|---|---|---|
| Foraging | 28 | −6.135 | 37.638 |
| 36 | −6.135 | 37.638 | |
| 38 | −6.135 | 37.638 | |
| Mfor = 33.250 | 31 | −6.135 | 37.638 |
| Farming | 32 | −4.385 | 19.228 |
| 33 | −4.385 | 19.228 | |
| Mfarm = 35.000 | 40 | −4.385 | 19.228 |
| Natural resources | 47 | 7.948 | 63.171 |
| 43 | 7.948 | 63.171 | |
| Mnr = 47.333 | 52 | 7.948 | 63.171 |
| Industrial | 40 | 4.615 | 21.298 |
| 47 | 4.615 | 21.298 | |
| Mind = 44.0001 | 45 | 4.615 | 21.298 |
| GM = 39.385 | SSbetween = 461.643 |
MASTERING THE FORMULA
 12-
12-
Notice that individual scores are never involved in the calculations, just sample means and the grand mean. Also notice that the first group (foraging), with four participants, has more weight in the calculation than the other three groups, which each have only three participants. The third column of Table 12-7 includes the deviations and the fourth includes the squared deviations. The between-
305
SSbetween = Σ(M − GM)2
Now is the moment of arithmetic truth. Were the calculations correct? To find out, we add the within-
MASTERING THE FORMULA
12-
SStotal = SSwithin + SSbetween = 629.062 = 167.419 + 461.643
Indeed, the total sum of squares, 629.074, is almost equal to the sum of the other two sums of squares, 167.419 and 461.643, which is 629.062. The slight difference is due to rounding decisions. So the calculations were correct.
To recap (Table 12-8), for the total sum of squares, we subtract the grand mean from each individual score to get the deviations. For the within-
| Sum of Squares | To calculate the deviations, subtract the… | Formula |
|---|---|---|
| Between- |
Grand mean from the sample mean (for each score) | SSbetween = Σ(M − GM)2 |
| Within- |
Sample mean from each score | SSwithin = Σ(X − M)2 |
| Total | Grand mean from each score | SStotal = Σ(X − GM)2 |
MASTERING THE FORMULA
 12-
12-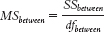 . For the within-
. For the within-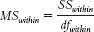
Now we insert these numbers into the source table to calculate the F statistic. See Table 12-9 for the source table that lists all the formulas and Table 12-10 for the completed source table. We divide the between-
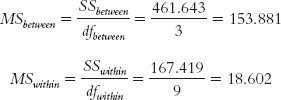

| Source | SS | df | MS | F |
|---|---|---|---|---|
| Between- |
461.643 | 3 | 153.881 | 8.27 |
| Within- |
167.419 | 9 | 18.602 | |
| Total | 629.074 | 12 |
We then divide the between-
MASTERING THE FORMULA
12-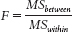 . We divide the between-
. We divide the between-
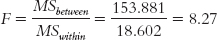
306
Making a Decision
Now we have to come back to the six steps of hypothesis testing for ANOVA to fill in the gaps in steps 1 and 6. We finished steps 2 through 5 in the previous section.
Step 1: ANOVA assumes that participants were selected from populations with equal variances. Statistical software, such as SPSS, tests this assumption while analyzing the overall data. For now, we can use the last column from the within-
| Sample | Foraging | Farming | Natural Resources | Industrial |
|---|---|---|---|---|
| Squared deviations: | 27.563 | 9.000 | 0.111 | 16.000 |
| 7.563 | 4.000 | 18.775 | 9.000 | |
| 22.563 | 25.000 | 21.781 | 1.000 | |
| 5.063 | ||||
| Sum of squares: | 62.752 | 38.000 | 40.667 | 26.000 |
| N − 1: | 3 | 2 | 2 | 2 |
| Variance | 20.917 | 19.000 | 20.334 | 13.000 |
307
Step 6: Now that we have the test statistic, we compare it with 3.86, the critical F value that we identified in step 4. The F statistic we calculated was 8.27, and Figure 12-4 demonstrates that the F statistic is beyond the critical value: We can reject the null hypothesis. It appears that people living in some types of societies are fairer, on average, than are people living in other types of societies. And congratulations on making your way through your first ANOVA! Statistical software will do all of these calculations for you, but understanding how the computer produced those numbers adds to your overall understanding.
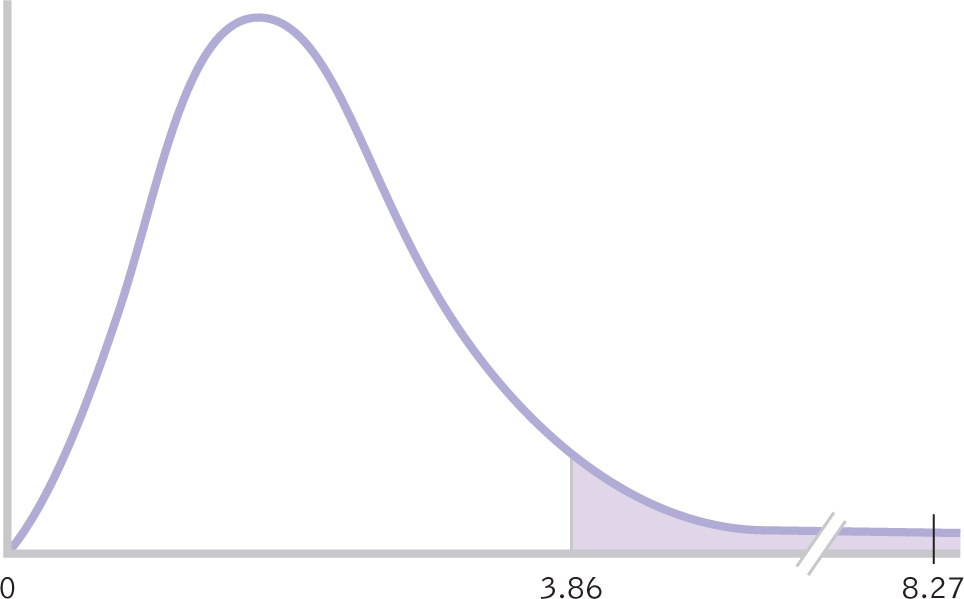
Figure 12-
The ANOVA, however, only allows us to conclude that at least one mean is different from at least one other mean. The next section describes how to determine which groups are different.
Summary: We reject the null hypothesis. It appears that mean fairness levels differ based on the type of society in which a person lives. In a scientific journal, these statistics are presented in a similar way to the z and t statistics but with separate degrees of freedom in parentheses for between-
CHECK YOUR LEARNING
Reviewing the Concepts
- One-
way between- groups ANOVA uses the same six steps of hypothesis testing that we learned in Chapter 7, but with a few minor changes in steps 3 and 5. - In step 3, we merely state the comparison distribution and provide two different types of degrees of freedom, df for the between-
groups variance and df for the within- groups variance. - In step 5, we complete the calculations, using a source table to organize the results. First, we estimate population variance by considering the differences among means (between-
groups variance). Second, we estimate population variance by calculating a weighted average of the variances within each sample (within- groups variance). - The calculation of variability requires several means, including sample means and the grand mean, which is the mean of all scores regardless of which sample the scores came from.
- We divide between-
groups variance by within- groups variance to calculate the F statistic.
A higher F statistic indicates less overlap among the sample distributions, evidence that the samples come from different populations. - Before making a decision based on the F statistic, we check to see that the assumption of equal sample variances is met. This assumption is met when the largest sample variance is not more than twice the amount of the smallest variance.
Clarifying the Concepts
- 12-
5 If the F statistic is beyond the cutoff, what does that tell us? What doesn’t that tell us? - 12-
6 What is the primary subtraction that enters into the calculation of SSbetween? - 12-
7 Calculate each type of degrees of freedom for the following data, assuming a between-groups design:
Group 1: 37, 30, 22, 29
Group 2: 49, 52, 41, 39
Group 3: 36, 49, 42- dfbetween = Ngroups − 1
- dfwithin = df1 + df2 +…+ dflast
- dftotal = dfbetween + dfwithin, or dftotal = Ntotal − 1
- 12-
8 Using the data in Check Your Learning 12-7, compute the grand mean. - 12-
9 Using the data in Check Your Learning 12-7, compute each type of sum of squares. - Total sum of squares
- Within-
groups sum of squares - Between-
groups sum of squares
- 12-
10 Using all of your calculations in Check Your Learning 12-7 to 12- 9, perform the simple division to complete an entire between- groups ANOVA source table for these data.
Applying the Concepts
- 12-
11 Let’s create a context for the data provided above. Hollon, Thase, and Markowitz (2002) reviewed the efficacy of different treatments for depression, including medications, electroconvulsive therapy, psychotherapy, and placebo treatments. These data re-create some of the basic findings they present regarding psychotherapy. Each group is meant to represent people who received a different psychotherapy- based treatment, including psychodynamic therapy in group 1, interpersonal therapy in group 2, and cognitive- behavioral therapy in group 3. The scores presented here represent the extent to which someone responded to the treatment, with higher numbers indicating greater efficacy of treatment. Group 1 (psychodynamic therapy): 37, 30, 22, 29
Group 2 (interpersonal therapy): 49, 52, 41, 39
Group 3 (cognitive-
behavioral therapy): 36, 49, 42 - Write hypotheses, in words, for this research.
- Check the assumptions of ANOVA.
- Determine the critical value for F. Using your calculations from Check Your Learning 12-
10, make a decision about the null hypothesis for these treatment options.
Solutions to these Check Your Learning questions can be found in Appendix D.