13.2 Beyond Hypothesis Testing for the One-Way Within-Groups ANOVA
Hypothesis testing with the one-
R2, the Effect Size for ANOVA
MASTERING THE FORMULA
 13-
13-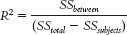 . We divide the between-
. We divide the between-
The calculations for R2 for a one-
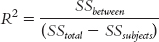
EXAMPLE 13.3
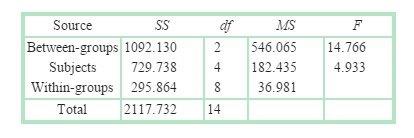
Let’s apply this to the ANOVA we just conducted. We can use the statistics in the source table above to calculate R2:
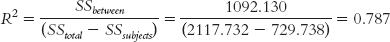
The conventions for R2 are the same as those shown in Table 12-12. This effect size of 0.79 is a very large effect: 79% of the variability in ratings of beer is explained by price.
Tukey HSD
EXAMPLE 13.4
We use the same procedure that we used for a one-
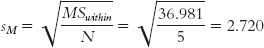
The standard error allows us to calculate HSD for each pair of means.
Cheap beer (34.4) versus mid-
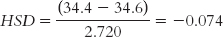
Cheap beer (34.4) versus high-
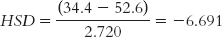
337
Mid-
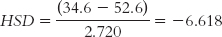
Now we look up the critical value in the q table in Appendix B. For a comparison of three means with within-

The q table indicates two statistically significant differences whose HSDs are beyond the critical values: −6.691 and −6.618. It appears that high-
What might explain these differences? It’s not surprising that expensive beers came out ahead of cheap and midrange beers, but Fallows was surprised that no observable average difference was found between cheap and mid-
How much faith can we have in these findings? As behavioral scientists, we critically examine the design and procedures. Did the darker color of Sam Adams (the beer that received the highest average ratings) give it away as a high-
Next Steps
Matched Groups
So far, we’ve learned two hypothesis tests that we can use when we have a within-
This research design is particularly useful when participants can’t be in two groups at the same time. For example, a matched-
338
Let’s look at a published example in the social science literature. Researchers in the state of Indiana in the United States compared depression levels of elderly Mexican American caregivers with elderly Mexican American noncaregivers (Hernandez & Bigatti, 2010). Sixty-
Using matched groups increases statistical power the same way that a within-
Second, if one of the people in a matched pair decides not to complete the study, then we must discard the data for the match for this person. This makes for less-
CHECK YOUR LEARNING
Reviewing the Concepts
- It is recommended, as it is for other hypothesis tests, that we calculate a measure of effect size, R2, for a one-
way within- groups ANOVA. - As with one-
way between- groups ANOVA, if we are able to reject the null hypothesis with a one- way within- groups ANOVA, we’re not finished. We must conduct a post hoc test, such as a Tukey HSD test, to determine exactly which pairs of means are significantly different from one another. - Matched pairs and matched groups allow us to use within-
groups designs even if different participants experience each level of the independent variable. Rather than using the same participants, we match different participants on possible confounding variables.
339
Clarifying the Concepts
- 13-
6 How does the calculation of the effect size R2 differ between the one-way within- groups ANOVA and the one- way between- groups ANOVA? - 13-
7 How does the calculation of the Tukey HSD differ between the one-way within- groups ANOVA and the one- way between- groups ANOVA?
Calculating the Statistics
- 13-
8 A researcher measured the reaction time of six participants at three different times and found the mean reaction time at time 1 (M1 = 155.833), time 2 (M2 = 206.833), and time 3 (M3 = 251.667). The researcher rejected the null hypothesis after performing a one-way within- groups ANOVA. For the ANOVA, dfbetween = 2, dfwithin = 10, and MSwithin = 771.256. - Calculate the HSD for each of the three mean comparisons.
- What is the critical value of q for this Tukey HSD test?
- For which comparisons do we reject the null hypothesis?
- 13-
9 Use the following source table to calculate the effect size R2 for the one-way within- groups ANOVA. Source SS df MS F Between 27,590.486 2 795.243 17.887 Subjects 16,812.189 5 3362.438 4.360 Within 7712.436 10 771.244 Total 52,115.111 17
Applying the Concepts
- 13-
10 In Check Your Learning 13-4 and 13- 5, we conducted an analysis of driver- experience ratings following test drives. - Calculate R2 for this ANOVA, and state what size effect this is.
- What follow-
up tests are needed for this ANOVA, if any?
Solutions to these Check Your Learning questions can be found in Appendix D.