Chapter 14 How it Works
14.1 Conducting A Two-Way Between-Groups ANOVA
The online dating Web site Match.com allows users to post personal ads to meet others. Each person is asked to specify a range from the youngest age that would be acceptable in a dating partner to the oldest acceptable age. The following data were randomly selected from the ads of 25-
- 25-
year- old women seeking men: 26, 24, 25, 24, 25 - 25-
year- old men seeking women: 18, 21, 22, 22, 18 - 25-
year- old women seeking women: 22, 25, 22, 25, 25 - 25-
year- old men seeking men: 23, 25, 24, 22, 20
There are two independent variables and one dependent variable. The first independent variable is gender of the seeker, and its levels are male and female. The second independent variable is gender of the person being sought, and its levels are men and women. The dependent variable is the youngest acceptable age of the person being sought. Based on these variables, how can we conduct a two-
| Female Seekers | Male Seekers | |
|---|---|---|
| Men sought | 24.8 | 22.8 |
| Women sought | 23.8 | 20.2 |
Here are the six steps of hypothesis testing for this example.
- Population 1 (female, men): Women seeking men. Population 2 (male, women): Men seeking women. Population 3 (female, women): Women seeking women. Population 4 (male, men): Men seeking men.
The comparison distributions will be F distributions. The hypothesis test will be a two-
way between- groups ANOVA. Assumptions: The data are not from random samples, so we must generalize with caution. The homogeneity of variance assumption is violated because the largest variance (3.70) is more than five times as large as the smallest variance (0.70). For the purposes of demonstration, we will proceed anyway. - The hypotheses for the main effect of the first independent variable, gender of seeker, is as follows: Null hypothesis: On average, male and female seekers report the same youngest acceptable ages for their partners—
H0: μM = μF. Research hypothesis: On average, male and female seekers report different youngest acceptable ages for their partners— H0: μM ≠ μF. The hypotheses for the main effect of the second independent variable, gender of person sought, is as follows: Null hypothesis: On average, those seeking men and those seeking women report the same youngest acceptable ages for their partners—
H0: μM = μW. Research hypothesis: On average, those seeking men and those seeking women report different youngest acceptable ages for their partners— H0: μM ≠ μW. The hypotheses for the interaction of gender of seeker and gender of person sought are as follows: Null hypothesis: The effect of the gender of the seeker on youngest acceptable ages for their partners does not depend on the gender of the person sought. Research hypothesis: The effect of the gender of the seeker on youngest acceptable ages for their partners does depend on the gender of the person sought.
- dfcolumns(seeker)= 2 − 1 = 1
dfrows(sought)= 2 − 1 = 1
dfinteraction= (1)(1) = 1
dfwithin = dfF,M + dfM,W + dfF,M + dfM,M = 4 + 4 + 4 + 4 = 16
Main effect of gender of seeker: F distribution with 1 and 16 degrees of freedom
Main effect of gender of sought: F distribution with 1 and 16 degrees of freedom
Interaction of seeker and sought: F distribution with 1 and 16 degrees of freedom
- Cutoff F for main effect of seeker: 4.49
Cutoff F for main effect of sought: 4.49
Cutoff F for interaction of seeker and sought: 4.49

Source SS df MS F Seeker gender 39.200 1 39.200 13.876 Sought gender 16.200 1 16.200 5.735 Seeker × sought 3.200 1 3.200 1.133 Within 45.200 16 2.825 Total 103.800 19 - There is a significant main effect of gender of the seeker and a significant main effect of gender of the person being sought. We can reject the null hypotheses for both of these main effects. Male seekers are willing to accept younger partners, on average, than are female seekers. Those seeking women are willing to accept younger partners, on average, than are those seeking men. We cannot reject the null hypothesis for the interaction; we can only conclude that there is not sufficient evidence that the effect of the gender of the seeker on youngest acceptable age depends on the gender of the person sought.
14.2 Calculating Effect Size For A Two-Way Between-Groups ANOVA
How can we compute and interpret the effect sizes, R2, for each main effect and the interaction for the ANOVA we conducted in How It Works 14.1? Here are the effect size calculations and interpretations, according to Cohen’s conventions, for each of the three effects.
For the main effect of seeker gender:
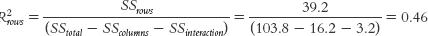
This is a large effect size.
For the main effect of sought gender:

This is a large effect size.
383
For the interaction:
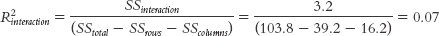
This is a medium effect size.