17.2 Chi-Square Tests
The chi-
The chi-
Hot-
Both chi-
465
MASTERING THE CONCEPT
17.2: When we only have nominal variables, we use the chi-
Chi-Square Test for Goodness of Fit
The chi-
EXAMPLE 17.1
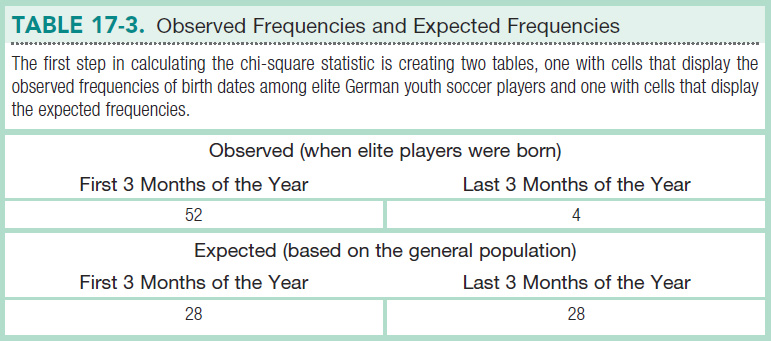
For example, researchers reported that the best youth soccer players in the world were more likely to have been born early in the year than later (Dubner & Levitt, 2006a). As one example, they reported that 52 elite youth players in Germany were born in January, February, or March, whereas only 4 players were born in October, November, or December. (Those born in other months were not included in this study.)
The null hypothesis predicts that when a person was born will not make any difference; the research hypothesis predicts that the month a person was born will matter when it comes to being an elite soccer player. Assuming that births in the general population are evenly distributed across months of the year, the null hypothesis posits equal numbers of elite soccer players born in the first 3 months and the last 3 months of the year. With 56 participants in the study (52 born in the first 3 months and 4 in the last 3 months), equal frequencies lead us to expect 28 players born in the first 3 months and 28 in the last 3 months just by chance. The birth months don’t appear to be evenly distributed, but is this a real pattern, or just chance?
Like previous hypothesis tests, the chi-
STEP 1: Identify the populations, distribution, and assumptions.
There are always two populations involved in a chi-

466
The first assumption is that the variable (birth month) is nominal. The second assumption is that each observation is independent; no single participant can be in more than one category. The third assumption is that participants were randomly selected. If not, it may be unwise to confidently generalize beyond the sample. A fourth assumption is that there is a minimum number of expected participants in every category (also called a cell)—at least 5 and preferably more. An alternative guideline (Delucchi, 1983) is for at least five times as many participants as cells. In any case, the chi-
Summary: Population 1: Elite German youth soccer players with birth dates like those we observed. Population 2: Elite German youth soccer players with birth dates like those in the general population.
The comparison distribution is a chi-
STEP 2: State the null and research hypotheses.
For chi-
Summary: Null hypothesis: Elite German youth soccer players have the same pattern of birth months as those in the general population. Research hypothesis: Elite German youth soccer players have a different pattern of birth months than those in the general population.
STEP 3: Determine the characteristics of the comparison distribution.
Our only task at this step is to determine the degrees of freedom. In most previous hypothesis tests, the degrees of freedom have been based on sample size. For the chi-
MASTERING THE FORMULA
17-
dfχ2 = k − 1
Here, k is the symbol for the number of categories. The current example has only two categories: Each soccer player in this study was born in either the first 3 months of the year or the last 3 months of the year:
dfχ2 = 2 − 1 = 1
Summary: The comparison distribution is a chi-
STEP 4: Determine the critical value, or cutoff.
To determine the cutoff, or critical value, for the chi-
467
| Proportion in Critical Region | |||
|---|---|---|---|
| df | 0.10 | 0.05 | 0.01 |
| 1 | 2.706 | 3.841 | 6.635 |
| 2 | 4.605 | 5.992 | 9.211 |
| 3 | 6.252 | 7.815 | 11.345 |
Summary: The critical χ2, based on a p level of 0.05 and 1 degree of freedom, is 3.841, as seen in the curve in Figure 17-1.
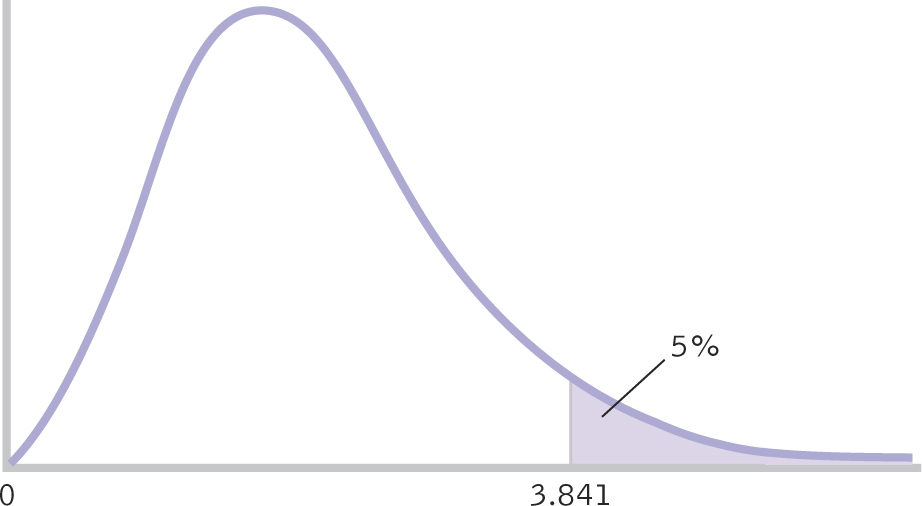
Figure 17-
STEP 5: Calculate the test statistic.
To calculate a chi-
(0.50)(56) = 28
468
| Column 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| Category | Observed (O) | Expected (E) | O − E | (O − E)2 |
|
| First 3 months | 52 | 28 | 24 | 576 | 20.571 |
| Last 3 months | 4 | 28 | −24 | 576 | 20.571 |
Of the 56 elite German youth soccer players in the study, we would expect to find that 28 were born in the first 3 months of the year (versus the last 3 months of the year) if these youth soccer players are no different from the general population with respect to birth date. Similarly, we would expect a proportion of 1 − 0.50 = 0.50 of these soccer players to be born in the last 3 months of the year:
(0.50)(56) = 28
These numbers are identical only because the proportions are 0.50 and 0.50. If the proportion expected for the first 3 months of the year, based on the general population, were 0.60, then we would expect a proportion of 1 − 0.60 = 0.40 for the last 3 months of the year.
The next step in calculating the chi-
As an example, here are the calculations for the category “first 3 months”:
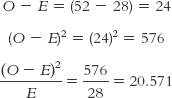
MASTERING THE FORMULA
 17-
17- . For each cell, we subtract the expected count, E, from the observed count, O. Then we square each difference and divide the square by the expected count. Finally, we sum the calculations for each of the cells.
. For each cell, we subtract the expected count, E, from the observed count, O. Then we square each difference and divide the square by the expected count. Finally, we sum the calculations for each of the cells.
Once we complete the table, the last step is easy. We just add up the numbers in the sixth column. In this case, the chi-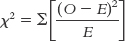
469
Summary: 
STEP 6: Make a decision.
This last step is identical to that of previous hypothesis tests. We reject the null hypothesis if the test statistic is beyond the critical value, and we fail to reject the null hypothesis if the test statistic is not beyond the critical value. In this case, the test statistic, 41.14, is far beyond the cutoff, 3.841, as seen in Figure 17-2. We reject the null hypothesis. Because there are only two categories, it’s clear where the difference lies. It appears that elite German youth soccer players are more likely to have been born in the first 3 months of the year, and less likely to have been born in the last 3 months of the year, than members of the general population. (If we had failed to reject the null hypothesis, we could only have concluded that these data did not provide sufficient evidence to show that elite German youth soccer players have a different likelihood of being born in the first, versus last, 3 months of the year than those in the general population.)
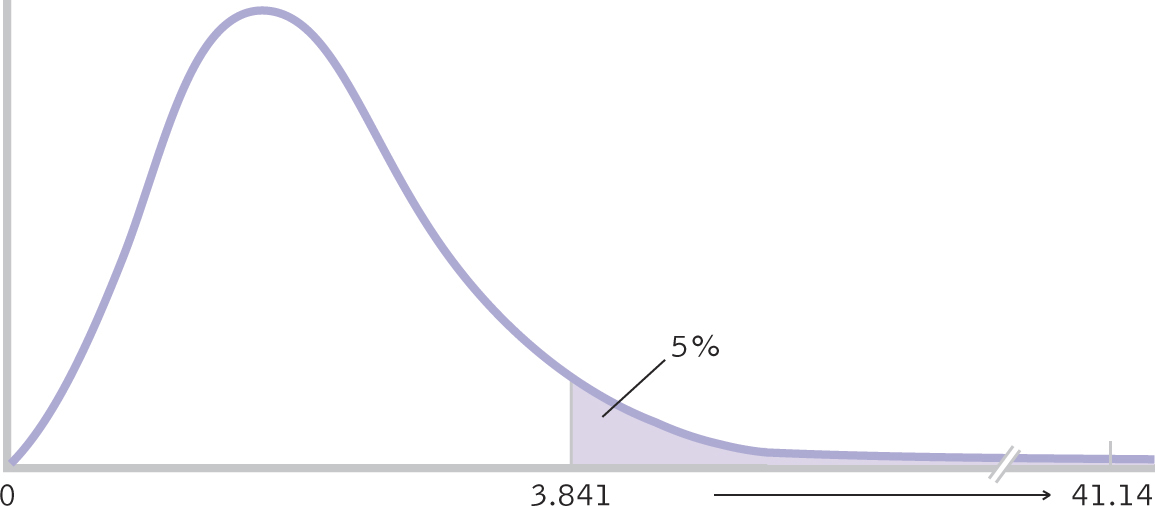
Figure 17-
Summary: Reject the null hypothesis; it appears that elite German youth soccer players are more likely to have been born in the first 3 months of the year, and less likely to have been born in the last 3 months of the year, than people in the general population.
We report these statistics in a journal article in almost the same format that we’ve seen previously. We report the degrees of freedom, the value of the test statistic, and whether the p value associated with the test statistic is less than or greater than the cutoff based on the p level of 0.05. (As usual, we would report the actual p level if we conducted this hypothesis test using software.) In addition, we report the sample size in parentheses with the degrees of freedom. In the current example, the statistics read:
χ2 (1, N = 56) = 41.14, p < 0.05
The researchers who conducted this study imagined four possible explanations: “a) certain astrological signs confer superior soccer skills; b) winter-
470
Dubner and Levitt (2006a) picked (d) and suggested another alternative. Participation in youth soccer leagues has a strict cutoff date: December 31. Compared to those born in December, children born the previous January are likely to be more physically and emotionally mature, perceived as more talented, chosen for the best leagues, and given better coaching—
Chi-Square Test for Independence

The chi-
Like the correlation coefficient, the chi-
EXAMPLE 17.2
In the clown study, as reported in the mass media (Ryan, 2006), 186 women were randomly assigned to receive IVF treatment only or to receive IVF treatment followed by 15 minutes of clown entertainment. Eighteen of the 93 who received only the IVF treatment became pregnant, whereas 33 of the 93 who received both IVF treatment and clown entertainment became pregnant. The cells for these observed frequencies can be seen in Table 17-5. The table of cells for a chi-
| Observed | ||
|---|---|---|
| Pregnant | Not pregnant | |
| Clown | 33 | 60 |
| No clown | 18 | 75 |
471
STEP 1: Identify the populations, distribution, and assumptions.
Population 1: Women receiving IVF treatment like the women we observed. Population 2: Women receiving IVF treatment for whom the presence of a clown is not associated with eventual pregnancy.
The comparison distribution is a chi-
STEP 2: State the null and research hypotheses.
Null hypothesis: Pregnancy rates are independent of whether one is entertained by a clown after IVF treatment. Research hypothesis: Pregnancy rates depend on whether one is entertained by a clown after IVF treatment.
STEP 3: Determine the characteristics of the comparison distribution.
For a chi-
dfrow = krow − 1
The degrees of freedom for the variable in the columns of the contingency table is:
dfcolumn = kcolumn − 1
The overall degrees of freedom is:
MASTERING THE FORMULA
 17-
17-
dfχ2 = (dfrow)(dfcolumn)
To expand this last formula, we write:
dfχ2 = (krow − 1)(kcolomn − 1)
The comparison distribution is a chi-
dfχ2 = (krow − 1)(kcolomn − 1) = (2 − 1)(2 − 1) = 1
STEP 4: Determine the critical values, or cutoffs.
The critical value, or cutoff, for the chi-
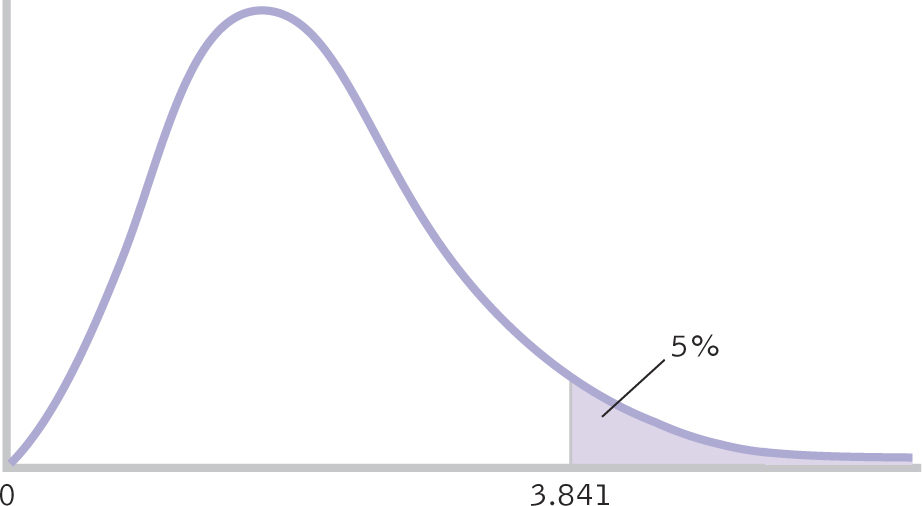
Figure 17-
STEP 5: Calculate the test statistic.
The next step, determining the appropriate expected frequencies, is the most important in the calculation of the chi-
472
But this would not make sense. Of the 186 women, only 51 became pregnant; 51/186 = 0.274, or 27.4%, of these women became pregnant. If pregnancy rates do not depend on clown entertainment, then we would expect the same percentage of successful pregnancies, 27.4%, regardless of exposure to clowns. If we have expected frequencies of 46.5 in all four cells, then we have a 50%, not a 27.4%, pregnancy rate. We must always consider the specifics of the situation.
In the current study, we already calculated that 27.4% of all women in the study became pregnant. If pregnancy rates are independent of whether a woman is entertained by a clown, then we would expect 27.4% of the women who were entertained by a clown to become pregnant and 27.4% of women who were not entertained by a clown to become pregnant. Based on this percentage, 100 − 27.4 = 72.6% of women in the study did not become pregnant. We would therefore expect 72.6% of women who were entertained by a clown to fail to become pregnant and 72.6% of women who were not entertained by a clown to fail to become pregnant. Again, we expect the same pregnancy and nonpregnancy rates in both groups—
Table 17-6 shows the observed data, and it also shows totals for each row, each column, and the whole table.
| Observed | |||
|---|---|---|---|
| Pregnant | Not pregnant | ||
| Clown | 33 | 60 | 93 |
| No clown | 18 | 75 | 93 |
| 51 | 135 | 186 | |
From Table 17-6, we see that 93 women were entertained by a clown after IVF treatment. As we calculated above, we would expect 27.4% of them to become pregnant:
(0.274)(93) = 25.482
Of the 93 women who were not entertained by a clown, we would expect 27.4% of them to become pregnant if clown entertainment is independent of pregnancy rates:
(0.274)(93) = 25.482
We now repeat the same procedure for not becoming pregnant. We would expect 72.6% of women in both groups to fail to become pregnant. For the women who were entertained by a clown, we would expect 72.6% of them to fail to become pregnant:
(0.726)(93) = 67.518
473
For the women who were not entertained by a clown, we would expect 72.6% of them to fail to become pregnant:
(0.726)(93) = 67.518
(Note that the two expected frequencies for the first row are the same as the two expected frequencies for the second row, but only because the same number of people were in each clown condition, 93. If these two numbers were different, we would not see the same expected frequencies in the two rows.)
The method of calculating the expected frequencies that we described above is ideal because it is directly based on our own thinking about the frequencies in the rows and in the columns. Sometimes, however, our thinking can get muddled, particularly when the two (or more) row totals do not match and the two (or more) column totals do not match. For these situations, a simple set of rules leads to accurate expected frequencies. For each cell, we divide its column total (Totalcolumn) by the grand total (N) and multiply that by the row total (Totalrow):
MASTERING THE FORMULA
17-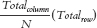 .
.
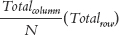
As an example, the observed frequency of those who became pregnant and were entertained by a clown is 33. The row total for this cell is 93. The column total is 51. The grand total, N, is 186. The expected frequency, therefore, is:

Notice that this result is identical to what we calculated without a formula. The middle step above shows that, even with the formula, we actually did calculate the pregnancy rate overall, by dividing the column total (51) by the grand total (186). We then calculated how many in that row of 93 participants we would expect to become pregnant using this overall rate:
(0.274)(93) = 25.482
The formula follows our logic, but it also keeps us on track when there are multiple calculations.
As a final check on the calculations, shown in Table 17-7, we can add up the frequencies to be sure that they still match the row, column, and grand totals. For example, if we add the two numbers in the first column, 25.482 and 25.482, we get 50.964 (different from 51 only because of rounding decisions). If we had made the mistake of dividing the 186 participants into cells by dividing by 4, we would have had 46.5 in each cell; then the total for the first column would have been 46.5 + 46.5 = 93, which is not a match with 51. This final check ensures that we have the appropriate expected frequencies in the cells.
| Expected | |||
|---|---|---|---|
| Pregnant | Not pregnant | ||
| Clown | 25.482 | 67.518 | 93 |
| No clown | 25.482 | 67.518 | 93 |
| 51 | 135 | 186 | |
474
The remainder of the fifth step is identical to that for a chi-
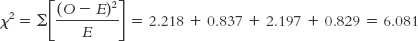
| Category | Observed (O) | Expected (E) | O − E | (O − E)2 |
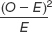
|
|---|---|---|---|---|---|
| Clown; pregnant | 33 | 25.482 | 7.518 | 56.520 | 2.218 |
| Clown; not pregnant | 60 | 67.518 | −7.518 | 56.520 | 0.837 |
| No clown; pregnant | 18 | 25.482 | −7.482 | 55.980 | 2.197 |
| No clown; not pregnant | 75 | 67.518 | 7.482 | 55.980 | 0.829 |
STEP 6: Make a decision.
Reject the null hypothesis; it appears that pregnancy rates depend on whether a woman receives clown entertainment following IVF treatment (Figure 17-4). The statistics, as reported in a journal article, would follow the format we learned for a chi-
χ2 (1, N = 186) = 6.08, p < 0.05
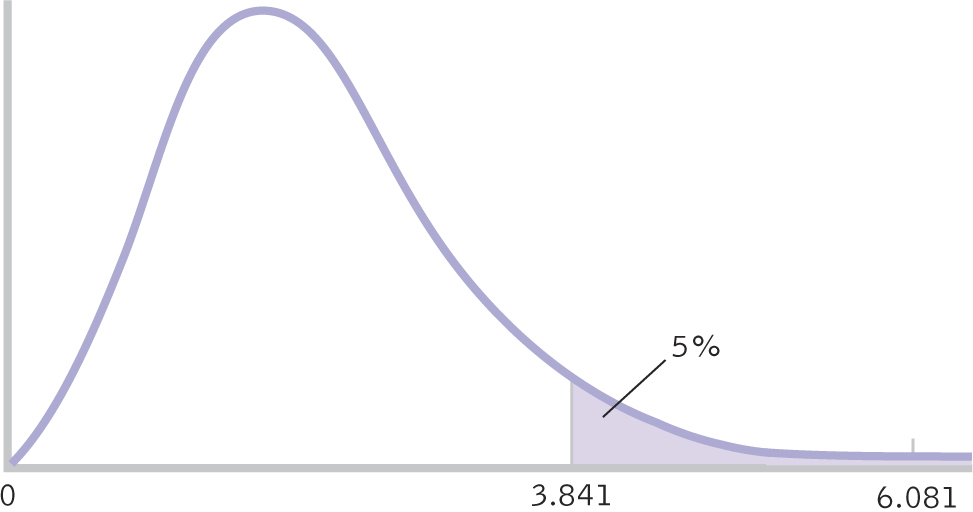
Figure 17-
475
CHECK YOUR LEARNING
Reviewing the Concepts
- The chi-
square tests are used when all variables are nominal. - The chi-
square test for goodness of fit is used with one nominal variable. - The chi-
square test for independence is used with two nominal variables; usually one can be thought of as the independent variable and one as the dependent variable. - Both chi-
square hypothesis tests use the same six steps of hypothesis testing with which we are familiar.
Clarifying the Concepts
- 17-
5 When do we use chi-square tests? - 17-
6 What are observed frequencies and expected frequencies?
Calculating the Statistics
- 17-
7 Imagine a town that boasts clear blue skies 80% of the time. You get to work in that town one summer for 78 days and record the following data. (Note: For each day, you picked just one label.)
Clear blue skies: 59 days
Cloudy/hazy/gray skies: 19 days- Calculate degrees of freedom for this chi-
square test for goodness of fit. - Determine the observed and expected frequencies.
- Calculate the differences and squared differences between frequencies, and calculate the chi-
square statistic. Use the six- column format provided here.
Category Observed (O) Expected (E) O−E (O−E)2 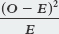
Clear blue skies Unclear skies - Calculate degrees of freedom for this chi-
Applying the Concepts
- 17-
8 The Chicago Police Department conducted a study comparing two types of lineups for suspect identification: simultaneous lineups and sequential lineups (Mecklenburg, Malpass, & Ebbesen, 2006). In simultaneous lineups, witnesses saw the suspects all at once, either live or in photographs, and then made their selection. In sequential lineups, witnesses saw the people in the lineup one at a time, either live or in photographs, and said yes or no to suspects one at a time. After numerous high-profile cases in which DNA evidence exonerated people who had been convicted, including many on death row, many police departments shifted to sequential lineups in the hope of reducing incorrect identifications. Several previous studies had indicated the superiority of sequential lineups with respect to accuracy. Over one year, three jurisdictions in Illinois compared the two types of lineups. Of 319 simultaneous lineups, 191 led to identification of the suspect, 8 led to identification of another person in the lineup, and 120 led to no identification. Of 229 sequential lineups, 102 led to identification of the suspect, 20 led to identification of another person in the lineup, and 107 led to no identification. - Who or what are the participants in this study? Identify the independent variable and its levels as well as the dependent variable and its levels.
- Conduct all six steps of hypothesis testing.
- Report the statistics as you would in a journal article.
- Why is this study an example of the importance of using two-
tailed rather than one- tailed hypothesis tests?
Solutions to these Check Your Learning questions can be found in Appendix D.
476