Chapter 18 How it Works

18.1 Calculating The Spearman Rank-Order Correlation Coefficient

The accompanying table includes ranks for accomplishment-related national pride, along with numbers of medals won at the 2000 Sydney Olympics for 10 countries. (Of course, this might not be the best way to operationalize the variable of Olympic performance; perhaps we should be ranking Olympic medals per capita.) How can we calculate the Spearman correlation coefficient for these two variables—seen in the first two columns of the accompanying table—pride rank and Olympic medals?

First, we have to convert the numbers of Olympic medals to ranks. Then we can calculate the correlation coefficient.

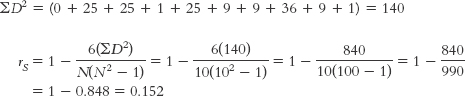
18.2 Conducting The Mann–Whitney U Test

The Mann-Whitney U test is the nonparametric version of the independent samples t test, so it is useful whenever we are comparing the rankings of two different groups. For example, we can use rankings to ask: In which of two regions in the United States do political science graduate programs tend to have the best rankings—on the East Coast (E) or in the Midwest (M)? Here are data from U.S. News & World Report’s 2013 online rankings of graduate schools. These are the top 18 doctoral programs in political science that are either on the East Coast or in the Midwest. (There are seven schools in other regions that are also in the top 25; they are omitted for the purposes of this example.) Schools listed at the same rank are tied.

How can we conduct a Mann–Whitney U test for this example? The independent variable is region of the country, and its levels are East Coast and Midwest. The dependent variable is U.S. News & World Report ranking.

1. This study meets the first and third of the three assumptions: (1) There are ordinal data after we convert the data from scale to ordinal. (2) The researchers did not use random selection, so the ability to generalize beyond this sample is limited. (3)There are some ties, but we will assume that there are not so many as to render the results of the test invalid.
2. Null hypothesis: Political science programs on the East Coast and those in the Midwest do not differ in national ranking. Research hypothesis: Political science programs on the East Coast and those in the Midwest differ in national ranking.
3. There are 10 top political science programs on the East Coast and 8 in the Midwest.
4. The cutoff, or critical value, for a Mann–Whitney U test with one group of 10 programs and one group of 8 programs, a p level of 0.05, and a two-tailed test is 17.

5. School	Rank	East Coast Rank	Midwest Rank
   Harvard University	1	1
   Princeton University	2	2
   University of Michigan, Ann Arbor	3.5		3.5
   Yale University	3.5	3.5
   Columbia University	5	5
   Massachusetts Institute of Technology	6	6
   Duke University	7	7
   University of Chicago	8		8
   University of North Carolina, Chapel Hill	9.5	9.5
   Washington University in St. Louis	9.5		9.5
   New York University	12.5	12.5
   The Ohio State University	12.5		12.5
   University of Rochester	12.5	12.5
   University of Wisconsin, Madison	12.5		12.5
   Cornell University	15.5	15.5
   University of Minnesota, Twin Cities	15.5		15.5
   Northwestern University	17		17
   University of Illinois, Urbana-Champaign	18		18

   Before we continue, we sum the ranks for each group and add subscripts to indicate which group is which:

   

   The formula for the first group is:

   

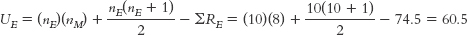
   The formula for the second group is:

   

6. For a Mann–Whitney U test, we compare only the smaller test statistic, 19.5, with the critical value, 17. This test statistic is not smaller than the critical value, so we fail to reject the null hypothesis. We cannot conclude that the two groups are different with respect to national rankings.

   In a journal article, the statistics would read:

   U = 19.5, p > 0.05