5.4 Type I and Type II Errors
Wrong decisions can be the result of unrepresentative samples. However, even when sampling has been properly conducted there are still two ways to make a wrong decision: 1) We can reject the null hypothesis when we should not have rejected it, or 2) we can fail to reject the null hypothesis when we should have rejected it. So let’s consider the two types of error using statistical language.
Type I Errors
A Type I error involves rejecting the null hypothesis when the null hypothesis is correct.
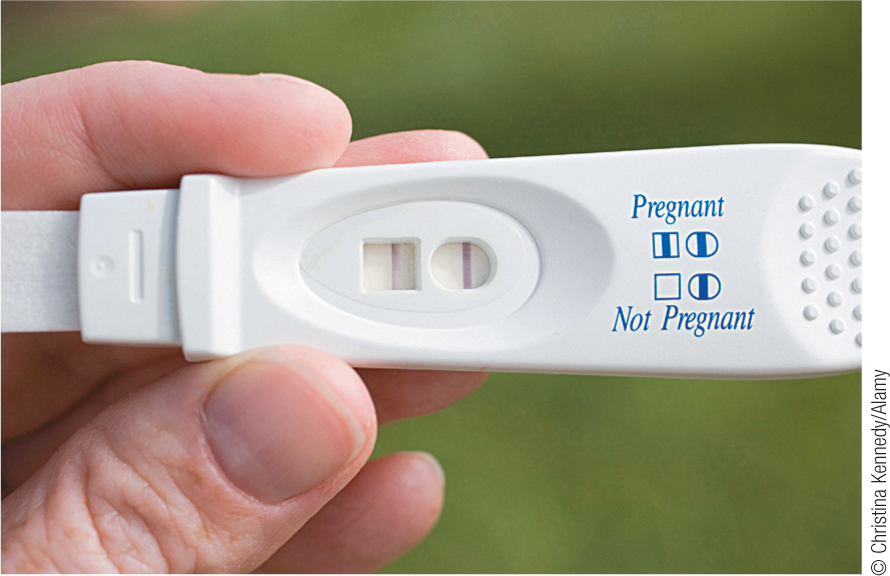
If we reject the null hypothesis, but it was a mistake to do so, then we have made a Type I error. Specifically, we commit a Type I error when we reject the null hypothesis but the null hypothesis is correct. A Type I error is like a false positive in a medical test. For example, if a woman believes she might be pregnant, then she might buy a home pregnancy test. In this case, the null hypothesis would be that she is not pregnant, and the research hypothesis would be that she is pregnant. If the test is positive, the woman rejects the null hypothesis—
116
A Type I error indicates that we rejected the null hypothesis falsely. As you might imagine, the rejection of the null hypothesis typically leads to action, at least until we discover that it is an error. For example, the woman with a false-
MASTERING THE CONCEPT
5.7: In hypothesis testing, there are two types of errors that we risk making. Type I errors, in which we reject the null hypothesis when the null hypothesis is true, are like false positives on a medical test; we think someone has a disease, but they really don’t. Type II errors, in which we fail to reject the null hypothesis when the null hypothesis is not true, are like false negatives on a medical test; we think someone does not have a disease, but they really do.
Type II Errors
A Type II error involves failing to reject the null hypothesis when the null hypothesis is false.
If we fail to reject the null hypothesis but it was a mistake to fail to do so, then we have made a Type II error. Specifically, we commit a Type II error when we fail to reject the null hypothesis but the null hypothesis is false. A Type II error is like a false negative in medical testing. In the pregnancy example earlier, the woman might get a negative result on the test and fail to reject the null hypothesis, the one that says she’s not pregnant. In this case, she would conclude that she’s not pregnant when she really is. A false negative is equivalent to a Type II error.
We commit a Type II error when we incorrectly failed to reject the null hypothesis. A failure to reject the null hypothesis typically results in a failure to take action, because a research intervention or a diagnosis is not received, which is generally less dangerous than incorrectly rejecting the null hypothesis. Yet there are cases in which a Type II error can have serious consequences. For example, the pregnant woman who does not believe she is pregnant because of a Type II error may drink alcohol in a way that unintentionally harms her fetus.
Next Steps
The Shocking Prevalence of Type I Errors
In the British Medical Journal, researchers observed that positive outcomes are more likely to be reported than null results (Sterne & Smith, 2001). First, researchers are less likely to want to publish null results, particularly if those results mean that a sponsoring pharmaceutical company’s favored drug did not receive support; an article in the New York Times described the biased outcome of that practice: “If I toss a coin, but hide the result every time it comes up tails, it looks as if I always throw heads” (Goldacre, 2013). Second, journals tend to publish “exciting” results, rather than “boring” ones (Sterne & Smith, 2001). To translate this into the terms of hypothesis testing, if a researcher rejects the “boring” null hypothesis, thus garnering support for the “exciting” research hypothesis, the editor of a journal is more likely to want to publish these results. Third, the mass media compound this problem; only the most exciting and surprising results are likely to get picked up by the national media and disseminated to the general public.
117
Using educated estimations, researchers calculated probabilities for 1000 hypothetical studies (Sterne & Smith, 2001). First, based on the literature on coronary heart disease, they assumed that 10% of studies should reject the null hypothesis; that is, 10% of studies were on medical techniques that actually worked. Second, based on flaws in methodology such as small sample sizes, as well as the fact that there will be chance findings, they estimated that half of the time the null hypothesis would not be rejected when it should be rejected, a Type II error. That is, half of the time, a helpful treatment would not receive empirical support. Finally, when the new treatment does not actually work, researchers would falsely reject the null hypothesis 5% of the time; just by chance, studies would lead to a false reportable difference between treatments, a Type I error. (In later chapters, we’ll learn more about this 5% cutoff, but for now, it’s only important to know that the 5% cutoff is arbitrary yet well established in statistical analyses.) Table 5-3 summarizes the researchers’ hypothetical outcomes of 1000 studies.
Of 1000 studies, the exciting research hypothesis would be accurate in only 100; for these studies, we should reject the null hypothesis. In the other 900 of these studies, the null hypothesis would be accurate and we should not reject the null hypothesis. But remember, we are sometimes incorrect in our conclusions. Given the 5% Type I error rate, we would falsely reject 5%, or 45, of the 900 null hypotheses that we should not reject. Given the 50% Type II error rate, we would incorrectly fail to reject 50 of the 100 studies in which we should reject the null hypothesis. (Both of the numbers indicating errors are in bold in Table 5-3.) The most important numbers are in the reject row—
| Result of Study | Null Hypothesis Is True (Treatment Doesn’t Work) | Null Hypothesis Is False (Treatment Does Work) | Total |
|---|---|---|---|
| Fail to reject | 855 | 50 | 905 |
| Reject | 45 | 50 | 95 |
| Total | 900 | 100 | 1000 |
Let’s consider an example. In recent years, there has been a spate of claims about the health benefits of natural substances. Natural health-
118
When the general public reads first of the value of vitamin E or echinacea and then of the health care establishment’s dismissal of these treatments, they wonder what to believe and often, sadly, rely even more on their own biased common sense. It would be far better for scientists to improve their research designs from the outset and reduce the Type I errors that so frequently make headlines.
CHECK YOUR LEARNING
Reviewing the Concepts
- When we draw a conclusion from inferential statistics, there is always a chance that we are wrong.
- When we reject the null hypothesis, but the null hypothesis is true, we have committed a Type I error.
- When we fail to reject the null hypothesis, but the null hypothesis is not true, we have committed a Type II error.
- Because of the flaws inherent in research, numerous null hypotheses are rejected falsely, resulting in Type I errors.
- The educated consumer of research is aware of her or his own biases and how they might affect her or his tendency to abandon critical thinking in favor of illusory correlations and the confirmation bias.
Clarifying the Concepts
- 5-
11 Explain how Type I and Type II errors both relate to the null hypothesis.
Calculating the Statistics
- 5-
12 If 7 out of every 280 people in prison are innocent, what is the rate of Type I errors? - 5-
13 If the court system fails to convict 11 out of every 35 guilty people, what is the rate of Type II errors?
Applying the Concepts
- 5-
14 Researchers conduct a study on perception by having participants throw a ball at a target first while wearing virtual-reality glasses and then while wearing glasses that allow normal viewing. The null hypothesis is that there is no difference in performance when wearing the virtual- reality glasses versus when wearing the glasses that allow normal viewing. - The researchers reject the null hypothesis, concluding that the virtual-
reality glasses lead to a worse performance than do the normal glasses. What error might the researchers have made? Explain. - The researchers fail to reject the null hypothesis, concluding that it is possible that the virtual-
reality glasses have no effect on performance. What error might the researchers have made? Explain.
- The researchers reject the null hypothesis, concluding that the virtual-
Solutions to these Check Your Learning questions can be found in Appendix D.
119