Chapter 6 How it Works
6.1 CONVERTING RAW SCORES TO z SCORES
Researchers reported that college students had healthier eating habits, on average, than did those who were neither college students nor college graduates (Georgiou et al., 1997). The researchers found that the 412 college students in the study ate breakfast a mean of 4.1 times per week, with a standard deviation of 2.4. Imagine that this is the entire population of interest.
Using symbolic notation and the formula, how can we calculate the z score for a student who eats breakfast six times per week? We can calculate the z score as follows:
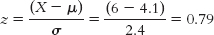
Now, how can we calculate the z score for a student who eats breakfast twice a week? We can calculate this z score as follows:
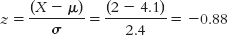
6.2 STANDARDIZATION WITH z SCORES AND PERCENTILES
Who is doing better financially—
For celebrities, the mean for the top 10 was $70.3 million, with a standard deviation of $41.4 million. Based on this, Kate Perry’s z score is:
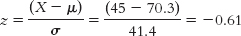
We can also calculate a range for her percentile rank. Fifty percent of scores fall below the mean. About 34% fall between the mean and a z score of −1.0, so: 50 − 34 = 16 percent of scores fall below a z score of −1. Therefore, Katy Perry is somewhere between the 16th and 50th percentiles among the top 10 most powerful celebrities.
For golf, the mean for the top 10 was $30.0 million, with a standard deviation of $21.1 million. Based on this, Tiger Woods’s z score is:
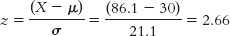
We can also estimate his percentile rank. Fifty percent of scores fall below the mean; about 34% fall between the mean and 1 standard deviation above the mean; and about 14% fall between 1 and 2 standard deviations above the mean: 50 + 34 + 14 = 98. Woods is above the 98th percentile among the top 10 golfers with the highest incomes.
Tiger Woods outearned Katy Perry when each was compared to the top 10 earners in their respective fields.