Chapter 8 How it Works

8.1 CALCULATING CONFIDENCE INTERVALS

The Graded Naming Test (GNT) asks respondents to name objects in a set of 30 black-and-white drawings in order to detect brain damage. The GNT population norm for adults in England is 20.4. Researchers wondered whether a sample of Canadian adults had different scores from adults in England (Roberts, 2003). If the scores were different, the English norms would not be valid for use in Canada. The mean for 30 Canadian adults was 17.5. Assume that the standard deviation of the adults in England is 3.2. How can we calculate a 95% confidence interval for these data?

Given μ = 20.4 and σ = 3.2, we can start by calculating standard error:

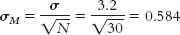
We then find the z values that mark off the most extreme 0.025 in each tail, which are −1.96 and 1.96. We calculate the lower end of the interval as:

Mlower = −z(σM) + Msample = −1.96(0.584) + 17.5 = 16.36

We calculate the upper end of the interval as:

Mupper = z(σM) + Msample = 1.96(0.584) + 17.5 = 18.64

The 95% confidence interval around the mean of 17.5 is [16.36, 18.64].

How can we calculate the 90% confidence interval for the same data? In this case, we find the z values that mark off the most extreme 0.05 in each tail, which are −1.645 and 1.645. We calculate the lower end of the interval as:

Mlower = −z(σM) + Msample = −1.645(0.584) + 17.5 = 16.54

We calculate the upper end of the interval as:

Mupper = z(σM) + Msample = 1.645(0.584) + 17.5 = 18.46

The 90% confidence interval around the mean of 17.5 is [16.54, 18.46].

What can we say about these two confidence intervals in comparison to each other? The range of the 95% confidence interval is larger than that of the 90% confidence interval. When calculating the 95% confidence interval, we are describing where we think a larger portion of our sample means will fall if we repeatedly select samples of this size from the same population (95% as opposed to 90%) so that we have a larger range within which those means are likely to fall.

214

8.2 CALCULATING EFFECT SIZE

The Graded Naming Test (GNT) study has a population norm for adults in England of 20.4. Researchers found a mean for 30 Canadian adults of 17.5, and we assumed a standard deviation of adults in England of 3.2 (Roberts, 2003). How can we calculate effect size for these data?

The appropriate measure of effect size for a z statistic is Cohen’s d, which is calculated as:

Based on Cohen’s conventions, this is a large effect size.