Chapter 8 Exercises
Clarifying the Concepts
Question 8.1
What specific danger exists when reporting a statistically significant difference between two means?
Question 8.2
In your own words, define the word confidence—first as you would use it in everyday conversation and then as a statistician would use it in the context of a confidence interval.
Question 8.3
Why do we calculate confidence intervals?
Question 8.4
What are the five steps to create a confidence interval for the mean of a z distribution?
Question 8.5
In your own words, define the word effect—first as you would use it in everyday conversation and then as a statistician would use it.
Question 8.6
What effect does increasing the sample size have on standard error and the test statistic?
Question 8.7
Relate effect size to the concept of overlap between distributions.
Question 8.8
What does it mean to say an effect-
Question 8.9
What are Cohen’s guidelines for small, medium, and large effects?
Question 8.10
How does statistical power relate to Type II errors?
Question 8.11
In your own words, define the word power—first as you would use it in everyday conversation and then as a statistician would use it.
Question 8.12
How are statistical power and effect size different but related?
Question 8.13
Traditionally, what minimum percentage chance of correctly rejecting the null hypothesis is suggested in order to proceed with an experiment?
Question 8.14
Explain how increasing alpha increases statistical power.
Question 8.15
List five factors that affect statistical power. For each, indicate how a researcher can leverage that factor to increase power.
Question 8.16
What are the four basic steps of a meta-
Question 8.17
What is the goal of a meta-
Question 8.18
Why is it important for a researcher who is conducting a meta-
Question 8.19
How does a file drawer analysis make the findings from a meta-
Question 8.20
In statistics, concepts are often expressed in symbols and equations. For Mlower = −z(σ) + Msample, (i) identify the incorrect symbol, (ii) state what the correct symbol is, and (iii) explain why the initial symbol was incorrect.
Question 8.21
In statistics, concepts are often expressed in symbols and equations. For 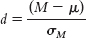
, (i) identify the incorrect symbol, (ii) state what the correct symbol is, and (iii) explain why the initial symbol was incorrect.
Calculating the Statistics
Question 8.22
In 2008, the Gallup poll asked people whether or not they were suspicious of steroid use among Olympic athletes. Thirty-
Question 8.23
In 2008, twenty-
Question 8.24
In 2013, the Gallup polling organization and the online publication Inside Higher Ed reported the results of a survey of 831 university presidents and chancellors. The report stated: “For results based on the sample size of 831 total respondents, one can say with 95 percent confidence that the margin of error attributable to sampling error is ±3.4 percentage points” (p. 6). Fourteen percent of respondents indicated that they strongly agreed that massive open online courses (MOOCs) could have a positive impact on higher education. Construct an interval estimate for the point estimate of 14%.
215
Question 8.25
For each of the following confidence levels, indicate how much of the distribution would be placed in the cutoff region for a one-
80%
85%
99%
Question 8.26
For each of the following confidence levels, indicate how much of the distribution would be placed in the cutoff region for a two-
80%
85%
99%
Question 8.27
For each of the following confidence levels, look up the critical z value for a one-
80%
85%
99%
Question 8.28
For each of the following confidence levels, look up the critical z values for a two-
80%
85%
99%
Question 8.29
Calculate the 95% confidence interval for the following fictional data regarding daily TV viewing habits: μ = 4.7 hours; σ = 1.3 hours; sample of 78 people, with a mean of 4.1 hours.
Question 8.30
Calculate the 80% confidence interval for the same fictional data regarding daily TV viewing habits: μ = 4.7 hours; σ = 1.3 hours; sample of 78 people, with a mean of 4.1 hours.
Question 8.31
Calculate the 99% confidence interval for the same fictional data regarding daily TV viewing habits: μ = 4.7 hours; σ = 1.3 hours; sample of 78 people, with a mean of 4.1 hours.
Question 8.32
Calculate the standard error for each of the following sample sizes when μ = 1014 and σ = 136:
12
39
188
Question 8.33
For a given variable, imagine we know that the population mean is 1014 and the standard deviation is 136. A sample mean of 1057 is obtained. Calculate the z statistic for this mean, using each of the following sample sizes:
12
39
188
Question 8.34
Calculate the effect size for the mean of 1057 observed in Exercise 8.33 where μ = 1014 and σ = 136.
Question 8.35
Calculate the effect size for each of the following average SAT math scores. Remember, SAT math is standardized such that μ = 500 and σ = 100.
61 people sampled have a mean of 480.
82 people sampled have a mean of 520.
6 people sampled have a mean of 610.
Question 8.36
For each of the effect-
61 people sampled have a mean of 480.
82 people sampled have a mean of 520.
6 people sampled have a mean of 610.
Question 8.37
For each of the following d values, identify the size of the effect, using Cohen’s guidelines.
d = 0.79
d = −0.43
d = 0.22
d = −0.04
Question 8.38
For each of the following d values, identify the size of the effect, using Cohen’s guidelines.
d = 1.22
d = −1.22
d = 0.13
d = −0.13
Question 8.39
For each of the following z statistics, calculate the p value for a two-
2.23
−1.82
0.33
Question 8.40
A meta-
Would a hypothesis test (assessing the null hypothesis that the average effect size is 0) lead us to reject the null hypothesis? Explain.
Use Cohen’s conventions to describe the average effect size of d = 0.11.
Question 8.41
A meta-
Question 8.42
Assume you are conducting a meta-
Calculate the mean effect size for these studies.
Use Cohen’s conventions to describe the mean effect size you calculated in part (a).
216
Applying the Concepts
Question 8.43
Distributions and the Burakumin: A friend reads in her Introduction to Psychology textbook about a minority group in Japan, the Burakumin, who are racially the same as other Japanese people but are viewed as outcasts because their ancestors were employed in positions that involved the handling of dead animals (e.g., butchers). In Japan, the text reported, mean IQ scores of Burakumin were 10 to 15 points below mean IQ scores of other Japanese. In the United States, where Burakumin experienced no discrimination, there was no mean difference (from Ogbu, 1986, as reported in Hockenbury & Hockenbury, 2013). Your friend says to you: “Wow—
Question 8.44
Sample size, z statistics, and the Consideration of Future Consequences scale: Here are summary data from a z test regarding scores on the Consideration of Future Consequences scale (Petrocelli, 2003): The population mean (μ) is 3.20 and the population standard deviation (σ) is 0.70. Imagine that a sample of students had a mean of 3.45.
Calculate the test statistic for a sample of 5 students.
Calculate the test statistic for a sample of 1000 students.
Calculate the test statistic for a sample of 1,000,000 students.
Explain why the test statistic varies so much even though the population mean, population standard deviation, and sample mean do not change.
Why might sample size pose a problem for hypothesis testing and the conclusions we are able to draw?
Question 8.45
Sample size, z statistics, and the Graded Naming Test: In an exercise in Chapter 7, we asked you to conduct a z test to ascertain whether the Graded Naming Test (GNT) scores for Canadian participants differed from the GNT norms based on adults in England. We also used these data in the How It Works section of this chapter. The mean for a sample of 30 adults in Canada was 17.5. The normative mean for adults in England is 20.4, and we assumed a population standard deviation of 3.2. With 30 participants, the z statistic was −4.97, and we were able to reject the null hypothesis.
Calculate the test statistic for 3 participants. How does the test statistic change compared to when N of 30 was used? Conduct step 6 of hypothesis testing. Does your conclusion change? If so, does this mean that the actual difference between groups changed? Explain.
Conduct steps 3, 5, and 6 for 100 participants. How does the test statistic change?
Conduct steps 3, 5, and 6 for 20,000 participants. How does the test statistic change?
What is the effect of sample size on the test statistic?
As the test statistic changes, has the underlying difference between groups changed? Why might this present a problem for hypothesis testing?
Question 8.46
Cheating with hypothesis testing: Unsavory researchers know that one can cheat with hypothesis testing. That is, they know that a researcher can stack the deck in her or his favor, making it easier to reject the null hypothesis.
If you wanted to make it easier to reject the null hypothesis, what are three specific things you could do?
Would it change the actual difference between the samples? Why is this a potential problem with hypothesis testing?
Question 8.47
Overlapping distributions and the LSATs: A Midwestern U.S. university reported that its behavioral science majors tended to outperform its humanities majors on the LSAT standardized test for law school admissions. Sadie, an English major, and Kofi, a sociology major, both just took the LSAT.
Can we tell which student will do better on the LSAT? Explain your answer.
Draw a picture that represents what the two distributions, that for social science majors and that for humanities majors at this institution, might look like with respect to one another.
Question 8.48
Confidence intervals, effect sizes, and tennis serves: Let’s assume the average speed of a serve in men’s tennis is around 135 mph, with a standard deviation of 6.5 mph. Because these statistics are calculated over many years and many players, we will treat them as population parameters. We develop a new training method that will increase arm strength, the force of the tennis swing, and the speed of the serve, we hope. We recruit 9 professional tennis players to use our method. After 6 months, we test the speed of their serves and compute an average of 138 mph.
Using a 95% confidence interval, test the hypothesis that our method makes a difference.
Compute the effect size and describe its strength.
Calculate statistical power using an alpha of 0.05, or 5%, and a one-
tailed test. Calculate statistical power using an alpha of 0.10, or 10%, and a one-
tailed test. Explain how power is affected by alpha in the calculations in parts (c) and (d).
217
Question 8.49
Confidence intervals and football wins: In an exercise in Chapter 7, we asked whether college football teams tend to be more likely or less likely to be mismatched in the upper National Collegiate Athletic Association (NCAA) divisions. During one week of a college football season, the population of 53 Football Bowl Subdivision (FBS; formerly Division I-
Calculate the 95% confidence interval for this sample.
State in your own words what we learn from this confidence interval.
What information does the confidence interval give us that we also get from a hypothesis test?
What additional information does the confidence interval give us that we do not get from a hypothesis test?
Question 8.50
Confidence intervals and football wins (continued): Using the football data presented in Exercise 8.49, practice evaluating data using confidence intervals.
Compute the 80% confidence interval.
How do the conclusion and the confidence interval change as you move from 95% confidence to 80% confidence?
Why don’t we talk about having 100% confidence?
Question 8.51
Effect size and football wins: In Exercises 8.49 and 8.50, we considered the study of week 11 of the fall 2006 college football season, during which the population of 53 FBS games had a mean spread (winning score minus losing score) of 16.189, with a standard deviation of 12.128. The sample of four games that were played that week in the next highest league, the FCS, had a mean of 8.75.
Calculate the appropriate measure of effect size for this sample.
Based on Cohen’s conventions, is this a small, medium, or large effect?
Why is it useful to have this information in addition to the results of a hypothesis test?
Question 8.52
Effect size and football wins (continued): In Exercise 8.51, you calculated an effect size for data from week 11 of the fall 2006 college football season with 4 games. Imagine that you had a sample of 20 games. How would the effect size change? Explain why it would or would not change.
Question 8.53
Confidence intervals, effect sizes, and Valentine’s Day spending: According to the Nielsen Company, Americans spend $345 million on chocolate during the week of Valentine’s Day. Let’s assume that we know the average married person spends $45, with a population standard deviation of $16. In February 2009, the U.S. economy was in the throes of a recession. Comparing data for Valentine’s Day spending in 2009 with what is generally expected might give us some indication of the attitudes during the recession.
Compute the 95% confidence interval for a sample of 18 married people who spent an average of $38.
How does the 95% confidence interval change if the sample mean is based on 180 people?
If you were testing a hypothesis that things had changed under the financial circumstances of 2009 as compared to in previous years, what conclusion would you draw in part (a) versus part (b)?
Compute the effect size based on these data and describe the size of the effect.
Question 8.54
More about confidence intervals, effect sizes, and tennis serves: Let’s assume the average speed of a serve in women’s tennis is around 118 mph, with a standard deviation of 12 mph. We recruit 100 amateur tennis players to use our method this time, and after 6 months we calculate a group mean of 123 mph.
Using a 95% confidence interval, test the hypothesis that our method makes a difference.
Compute the effect size and describe its strength.
Question 8.55
Confidence intervals, effect sizes, and tennis serves (continued): As in the previous exercise, assume the average speed of a serve in women’s tennis is around 118 mph, with a standard deviation of 12 mph. But now we recruit only 26 amateur tennis players to use our method. Again, after 6 months we calculate a group mean of 123 mph.
Using a 95% confidence interval, test the hypothesis that our method makes a difference.
Compute the effect size and describe its strength.
How did changing the sample size from 100 (in Exercise 8.54) to 26 affect the confidence interval and effect size? Explain your answer.
Question 8.56
In several exercises in this chapter, we considered the study of week 11 of the fall 2006 college football season, during which the population of 53 FBS games had a mean spread (winning score minus losing score) of 16.189, with a standard deviation of 12.128. The sample of four games that were played that week in the next-
Calculate statistical power for this study using a one-
tailed test and a p level of 0.05. What does the statistical power suggest about how we should view the findings of this study?
218
Using G*Power or an online power calculator, calculate statistical power for this study for a one-
tailed test with a p level of 0.05.
Question 8.57
Calculate statistical power based on the data presented in Exercise 8.55 using the following alpha levels in a one-
Alpha of 0.05, or 5%
Alpha of 0.10, or 10%
Explain how power is affected by alpha in these calculations.
Question 8.58
Meta-
In this article, we use meta-
Question 8.59
Meta-
Many previous authors have advocated traditional mental health treatments be modified to better match clients’ cultural contexts. Numerous studies evaluating culturally adapted interventions have appeared, and the present study used meta-
What is the topic chosen by the researchers conducting the meta-
analysis? What type of effect size statistic did the researchers’ calculate for each study in the meta-
analysis? What was the mean effect size? According to Cohen’s conventions, how large is this effect?
If a study chosen for the meta-
analysis did not include an effect size, what summary statistics could the researchers use to calculate an effect size?
Question 8.60
Meta-
Across all 76 studies, the random effects weighted average effect size was d = .45 (SE = .04, p < .0001), with a 95% confidence interval of d = .36 to d = .53. The data consisted of 72 nonzero effect sizes, of which 68 (94%) were positive and 4 (6%) were negative. Effect sizes ranged from d = −48 to d = 2.7 (Griner & Smith, 2006, p. 535).
What is the confidence interval for the effect size?
Based on the confidence interval, would a hypothesis test lead us to reject the null hypothesis that the effect size is zero? Explain.
Why would a graph, such as a histogram, be useful when conducting a meta-
analysis like this one? (Hint: Consider the problems when using a mean as the measure of central tendency.)
Putting It All Together
Question 8.61
Fantasy baseball: Your roommate is reading Fantasyland: A Season on Baseball’s Lunatic Fringe (Walker, 2006) and is intrigued by the statistical methods used by competitors in fantasy baseball leagues (in which competitors select a team of baseball players from across all major league teams, winning in the fantasy league if their eclectic roster of players outperforms the chosen mixes of other fantasy competitors). Among the many statistics reported in the book is a finding that Major League Baseball (MLB) players who have a third child show more of a decline in performance than players who have a first child or a second child. Your friend remembers that Red Sox player David Ortiz has three children and drops him from consideration for his fantasy team.
Explain to your friend why a difference between means doesn’t provide information about any specific individual player. Include a drawing of overlapping curves as part of your answer. On the drawing, mark places on the x-axis that might represent a player from the distribution of those who recently had a third child (mark with an X) scoring above a player from the distribution of those who recently had a first or second child (mark with a Y).
Explain to your friend that a statistically significant difference doesn’t necessarily indicate a large effect size. How might a measure of effect size, such as Cohen’s d, help us understand the importance of these findings and compare them to other predictors of performance that might have larger effects?
Given that the reported association is true, can we conclude that having a third child causes a decline in performance? Explain your answer. What confounding variables might lead to the difference observed in this study?
Given the relatively limited numbers of MLB players (and the relatively limited numbers of those who recently had a child—
whether first, second, or third), what general guess would you make about the likely statistical power of this analysis?
219
Question 8.62
Hours of sleep: The table below provides information about hours of sleep.
| Mean of population 1 (from which the sample comes) | 14.9 hours of sleep |
| Sample size | 37 infants |
| Mean of population 2 | 16 hours of sleep |
| Standard deviation of the population | 1.7 hours of sleep |
| Standard error |
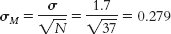
|
Calculate statistical power for a one-
tailed test (α = 0.05, or 5%) aimed at determining if those in the sample sleep fewer hours, on average, than those in the population. Recalculate statistical power with alpha of 0.01, or 1%. Explain why changing alpha affects power. Explain why we should not use a larger alpha to increase power.
Without performing any computations, describe how statistical power is affected by performing a two-
tailed test for this example. Why are two- tailed tests recommended over one- tailed tests? The easiest way to affect the outcome of a hypothesis test is to increase sample size. Similarly, true results may sometimes be missed because a sufficient sample was not used in the research. Perform the hypothesis test on these data with a sample of 37. Then perform the same hypothesis test but assume that the mean was based on only 4 infants.
The easiest way to increase statistical power is to increase sample size. Similarly, statistical power decreases with a smaller sample size. For these data, compute the statistical power of the one-
tailed statistical test with alpha of 0.05 when N is 4. How does that value compare to when N was 37?
Question 8.63
Effect size and an intervention to increase college applications: Caroline Hoxby and Sarah Turner (2013) conducted an experiment to determine whether a simple intervention could increase the number of college applications among low-
| Dependent variable | Effect in percentage change | Effect in effect size |
|---|---|---|
| Number of applications submitted | 19.0% | 0.247 |
Describe the sample and population of this study.
What is the independent variable and what are its levels?
What is the dependent variable?
The finding was statistically significant. Why is this not sufficient to determine that this intervention, which costs about $6 per student, is worthwhile?
What is the effect sizes for the dependent variable? How large is it, according to Cohen’s conventions?
What does this effect size mean in terms of standard deviations in the context of this study?
The researchers also included the effect in percentage change. Explain what this means in the context of this study.