Chapter 1. Impact 3.2
Impact…ON MATERIALS SCIENCE: I3.2 Crystal defects
The Third Law implies that at T = 0 perfectly crystalline substances are characterized by long-range, regularly repeating arrangements of atoms, ions, or molecules. This regularity, and the accompanying inter- and intramolecular interactions between the subunits of the crystal, govern the physical, optical, and electronic properties of the solid. In reality, however, all crystalline solids possess one or more defects that affect the physical and chemical properties of the substance. In fact, impurities are often introduced to achieve particular desirable properties, such as the colour of a gemstone or enhanced strength of a metal.
One of the main types of crystalline imperfection is a point defect, a location where an atom is missing or irregularly placed among other atoms in the crystal. Many gemstones feature ‘substitutional solids’, such as in rubies and blue sapphires in which the Al3+ ions in the corundum structure of alumina are replaced with Cr3+ and Fe3+ ions, respectively. Another type is one in which atoms are present in the gaps, the interstices, between the other atoms, and not replacing them. These ‘interstitial solids’ can result from the random diffusion of the dopants, the introduced species, into the voids. They can also result from self-diffusion, as in ionic crystals, where one of the ions normally present leaves its location and migrates into a void. The vacancy the departing ion leaves behind is known as a ‘Frenkel defect’.
Figure I3.2 illustrates the impact of impurities on the heat capacity and thus entropy of a pure crystal, in this case of the metal niobium, which is a component of the alloys that have the property of superconductivity below a certain critical temperature, the ability to conduct electricity with zero resistance. Niobium has become the dominant metal in low-temperature superconductor alloys because it can be manufactured economically in a ductile form that is needed for the high critical current of a superconductor. The purity of the metal, however, is essential to yield superconducting properties. Close to 1 K the heat capacity of pure niobium follows the Debye-T3 law. However, when niobium is treated by allowing H2 or D2 to diffuse over the sample at 700 °C impurities are introduced and the heat capacity diverges from that of the pure metal. To identify the role of the defects the values of Cp for the pure metal are subtracted from those of the doped samples, divided by T, and plotted against temperature. The area under the resulting curves then represents the contributions to the entropy from the presence of the impurities.
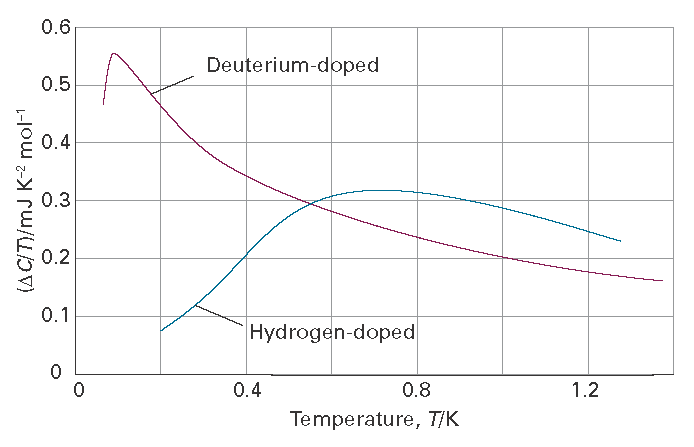
Figure I3.2 Molar heat capacity contributions of the defects in hydrogen- and deuterium-doped niobium. The area under each curve is used to calculate the entropy due to the presence of the defects. (Based on G. J. Sellers and A. C. Anderson, Phys. Rev. B. 10, 2771 (1974).)