14.0.2 14.3: Populations can grow quickly for a while, but not forever.

In a stable population, how many of the five million eggs laid by a female cod over the course of her life survive and grow to adulthood? How many of an elephant’s babies survive to adulthood and reproduce? These may seem like difficult questions to answer, requiring complex mathematical models of population growth and special knowledge about cod or elephants. But actually, the most fundamental fact about population growth is ridiculously simple.

How many of the female cod’s eggs and the female elephant’s babies will, on average, make it to adulthood? Just two.

If a population is not growing, each individual is ultimately replacing itself with a new individual. This is true for all species. Two of those cod eggs will make it. And two of those baby elephants will make it. For a stable population, on average two survive, rather than one, because both a male and a female contributed to each offspring. If each pair produced only one surviving offspring, the population would get smaller and smaller. But what happens to the rest of the cod eggs and elephant offspring? Along the way from gamete to adult, they may not survive. For example, an egg may not get fertilized. Or a fertilized egg may not survive to give rise to an offspring. Predation and other factors may prevent a youngster’s surviving to adulthood. Or an adult may not find a mate. There are too many risks to name them all.

What would happen if more than two cod or two elephants survived? If there were more than one offspring per individual, the population would grow until the earth was covered with cod, elephants, and every other species. But that hasn’t happened, and it can’t. Let’s investigate why.

We start by figuring out how a population grows if each individual does more than just “replace” itself. To calculate the growth rate of a population—the change in the number of individuals in the population in some unit of time, such as a year—we need two pieces of information: the number of individuals in the population now, N, and the per capita growth rate, r, which is simply the birth rate minus the death rate. The growth of the population in a year is the growth rate times the number of individuals present to start with: r × N.

If the birth rate is greater than the death rate, the population gets bigger. If the death rate is bigger than the birth rate, the population gets smaller. For example, if there are 500 individuals in a population (N = 500) and, over the course of a year, 125 offspring are born, the birth rate is 125 / 500, or 0.25 births per individual. And if 25 of the 500 individuals die during the same year, the death rate is 25 / 500, or 0.05 deaths per individual. In this population, the growth rate, r, is 0.25 − 0.05, or 0.20 individuals per individual per year. But how many individuals is that?

Since there were 500 individuals to start with, the population would increase by 0.20 × 500, or 100 individuals, during a year (the time period observed). After a second year, if it grew at the same rate, the population growth would be 0.20 × 600, or 120 new individuals. This would mean the population now has 720 individuals.

With the same calculations, we could predict the population size for the next 10, 50, or even 100 years (FIGURE 14-4). When a population’s size increases at a rate proportional to its current size—in other words, the bigger the population, the faster it grows—the growth is called exponential growth. As the J-shaped graph reveals, the size of a population growing exponentially becomes astronomical very quickly. In 10 years, the population of 500 elk would grow to 2,580. In 50 years, it would reach almost four million, and after 80 years it would surpass a billion individuals. It’s clear that unchecked exponential population growth ends badly.

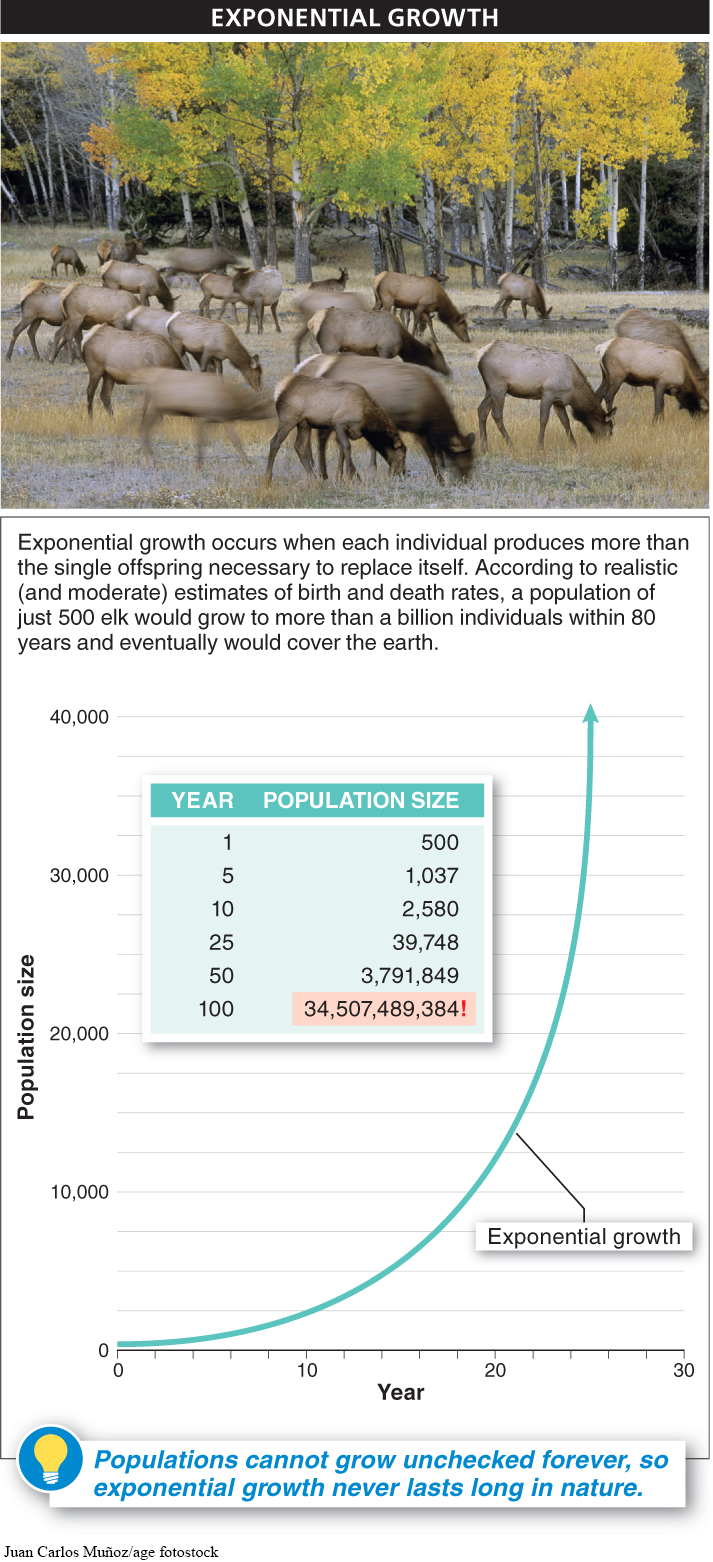
But the world isn’t overrun with cod or elephants or elk, so, clearly, exponential growth doesn’t occur for long. In the next section, we explore why populations cannot keep growing unchecked forever.