
Chapter 14. Chapter 14 Graphic Content
Introduction

Instructions
Review the information provided in the graph to answer each question below.
After submitting your answer, you will be provided feedback to check if your response is correct.
(This activity contains 7 questions.)
1.
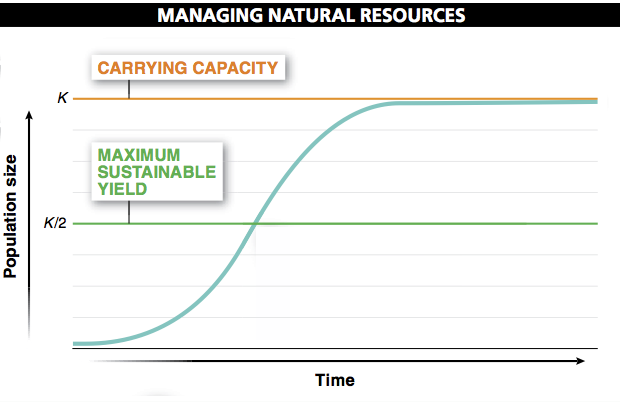
1. What is the purpose of this graph?
2.

2. What factors contribute to the blue line becoming flat?
3.

3. When the population reaches the carrying capacity, it appears to persist indefinitely. How is that possible? Do organisms stop dying?
4.

4. What data are represented in the graph?
5.

5. What could be added to this graph to improve it?
6.

6. Describe two assumptions about population growth that are implicit in this figure.
7.

7. If you were to create an alternative graph showing the relationship between population size (on the x-axis) and growth rate (on the y-axis), what would this graph look like? Write a description below.
Activity results are being submitted...