The cross product

Chapter 1. The cross product

10.1 – Introduction to the cross product

true

The dot product, described in the previous tutorial, is only one way to multiply two vectors. We can also multiply two vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ using the cross product.

This operation is written as

$\overrightarrow{C} = \overrightarrow{A} \times \overrightarrow{B}$

In the equation, the symbol “×” represents the mathematical operation known as the cross product.

Note: The result of taking the cross product of two vectors is another vector, whereas taking the dot product of two vectors (see tutorial 9) results in a scalar quantity.

The magnitude of the resulting vector from a cross product is equal to the product of the magnitudes of the two vectors and the sine of the angle between them.

$C=| \overrightarrow{A} \times \overrightarrow{B}|=AB{\,}\mathtt{sin}\, \phi$

The cross product of two vectors, $\overrightarrow{A}$ and $\overrightarrow{B}$ is always a vector perpendicular both $\overrightarrow{A}$ and $\overrightarrow{B}$ , as we can see in the picture:

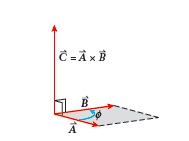
The cross product is a vector $\overrightarrow{C}$ that is perpendicular to both $\overrightarrow{A}$ and $\overrightarrow{B}$ , and has a magnitude AB sin ϕ, which equals the area of the parallelogram shown.

Note: The order of the two vectors in a cross product makes a difference. The cross product of $\overrightarrow{B}$ and $\overrightarrow{A}$ is the negative of the cross product of $\overrightarrow{A}$ and $\overrightarrow{B}$ or

$\overrightarrow{A} \times \overrightarrow{B} = -\overrightarrow{B} \times \overrightarrow{A}$

This results from the definition of the angle ϕ shown in the diagram - ϕ is directed from the first vector ( $\overrightarrow{A}$ ) to the second vector ( $\overrightarrow{B}$ ). If you travel the angle from the second vector to the first—in reverse direction, -ϕ becomes negative. The sine of a negative angle is also negative so calculating the cross product will give a negative answer.

Cross products are distributive, so $\overrightarrow{A} \times ( \overrightarrow{B} + \overrightarrow{C}) = \overrightarrow{A} \times \overrightarrow{B} + \overrightarrow{A} \times \overrightarrow{C}$

10.2 – Determining the direction of a cross product

Finding the direction of
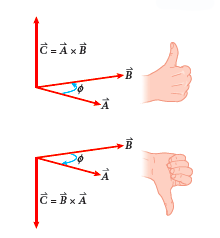
a cross product - Take a
minute to practice this
for

$\overrightarrow{A} \times \overrightarrow{B}$ and

$\overrightarrow{B} \times \overrightarrow{A}$ . Do
you get opposite
directions for the

$\overrightarrow{C}$ vector?

To determine the direction of the cross product

$\overrightarrow{C} = \overrightarrow{A} \times \overrightarrow{B}$ , you can use the right-hand rule.

How to do it:

1. Point the fingers of your right hand in the direction of the first vector of the cross product (in this case $\overrightarrow{A}$ ).

2. Then curl your fingers toward the second vector, $\overrightarrow{B}$ . If you stick your thumb straight out, it points in the direction of the cross product, vector $\overrightarrow{C}$ (the picture to the left may help).

If you instead want to find the direction of the cross product $\overrightarrow{B} \times \overrightarrow{A}$ , begin by pointing the fingers of your right hand in the direction of vector $\overrightarrow{B}$ . Then curl them toward vector $\overrightarrow{A}$ . Your thumb again points in the direction of the cross product.

Notice that using this method $\overrightarrow{A} \times \overrightarrow{B}$ gives the opposite direction to $\overrightarrow{B} \times \overrightarrow{A}$ as expected!

10.3 – The cross product – special cases

There are two special cases of the cross product that are worth pointing out.

1.The cross product of perpendicular vectors

In this case, the angle between the vectors, ϕ = 90°, so sin ϕ = 1

Therefore the magnitude of the cross product of perpendicular vectors is equal to:

$|\overrightarrow{A} \times \overrightarrow{B}|=AB{\,}\mathtt{sin}{\,}90°=AB(1)=AB$

2.The cross product of parallel vectors

In this case, the angle between the vectors, ϕ = 0°, so Sin ϕ = 0

Therefore the magnitude of the cross product of parallel vectors is equal to:

$|\overrightarrow{A} \times \overrightarrow{B}|=AB{\,}\mathtt{sin}{\,}0=AB(0)=0$

One example of this is the cross product of a vector with itself, $\overrightarrow{A} \times \overrightarrow{A}$ = 0.

Try it yourself 1

Evaluate the magnitude of the following cross products,

Question Sequence

Question 1.

$\overrightarrow{A} \times \overrightarrow{B}$ , where $\overrightarrow{A}$ is a vector of magnitude, 3 in the x direction and $\overrightarrow{B}$ is a vector of magnitude 5 in the y direction.

Try again.

Correct.

Incorrect.

Question 2.

$\overrightarrow{C} \times \overrightarrow{B}$ , where $\overrightarrow{B}$ is a vector of magnitude 10 in the y direction and $\overrightarrow{C}$ is a vector of magnitude 6 in the z direction.

Try again. Remember magnitudes are always positive.

Correct.

Incorrect.

Question 3.

$\overrightarrow{A} \times \overrightarrow{B}$ , where $\overrightarrow{A}$ is a vector of magnitude 3 in the x direction and $\overrightarrow{B}$ is a vector of magnitude 3 in the x direction.

Try again. What is the cross product of parallel vectors?

Correct.

Incorrect.

Worked Example

Try it yourself 2

Question Sequence

Question 4.

For Questions 4-8:
Vector $\overrightarrow{A}$ has components, A_x = 2, A_y = 2, A_z = 0
Vector $\overrightarrow{B}$ has components B_x = 7, B_y = 0, B_z = 0

What is the magnitude of vector $\overrightarrow{A}$ ?

Try again. Find the resultant vector of A_x and A_y.

Correct.

Incorrect.

Question 5.

What is the magnitude of vector $\overrightarrow{B}$ ?

Try again.

Correct.

Incorrect.

Question 6.

What is the angle between $\overrightarrow{A}$ and $\overrightarrow{B}$ ?

Try again. Use a sketch to figure this out.

Correct.

Incorrect.

Question 7.

Find the magnitude of the cross product $\overrightarrow{A} \times \overrightarrow{B}$ ?

Try again. Use your answers from Questions 4-6 for this part.

Correct.

Incorrect.

Question 8.

What is the direction of the vector solution of $\overrightarrow{A} \times \overrightarrow{B}$ ?

The x direction

The y direction

The z direction

The direction can’t be found

Try again.

Correct.

Incorrect.

Question 9.

For Questions 9-12:Calculate the magnitude of the cross product, $\overrightarrow{A} \times \overrightarrow{B}$ if vector $\overrightarrow{A}$ has components, Ax = 5, Ay = 5, Az = 0 and vector $\overrightarrow{B}$ has components Bx = 2, By = 3, Bz = 0

What is the magnitude of vector $\overrightarrow{A}$ ?

Try again.

Correct.

Incorrect.

Question 10.

What is the magnitude of vector $\overrightarrow{B}$ ?

Try again.

Correct.

Incorrect.

Question 12.

Calculate the magnitude of the cross product $\overrightarrow{A} \times \overrightarrow{B}$ .

Try again.

Correct.

Incorrect.

Question 13.

Calculate the magnitude of the cross product, $\overrightarrow{A} \times \overrightarrow{B}$ if vector $\overrightarrow{A}$ has components, A_x = 2, A_y = 0, A_z = 0 and vector $\overrightarrow{B}$ has components B_x = 0, B_y = 4, B_z = 0

Try again. Notice that the two vectors

$\overrightarrow{A}$ and

$\overrightarrow{B}$ are perpendicular.

Correct.

Incorrect.

Question 14.

Calculate the magnitude of the cross product, $\overrightarrow{A} \times \overrightarrow{B}$ if vector $\overrightarrow{A}$ has components, A_x = -2, A_y = 3, A_z = 0 and vector $\overrightarrow{B}$ has components B_x = 2, B_y = 2, B_z = 0

Try again.

Correct.

Incorrect.

Chapter 1. The cross product

Instructions

10.1 – Introduction to the cross product

10.2 – Determining the direction of a cross product

10.3 – The cross product – special cases

Try it yourself 1

Question Sequence

Question 1.

Question 2.

Question 3.

Worked Example

Try it yourself 2

Question Sequence

Question 4.

Question 5.

Question 6.

Question 7.

Question 8.

Question 9.

Question 10.

Question 11.

Question 12.

Question 13.

Question 14.