Chapter 1. Equations

Introduction to Equations

true

An equation is a statement written using numbers and symbols to indicate that two quantities, written on either side of an equal sign (=), are equal. The quantity on either side of the equal sign may consist of a single term, or of a sum or difference of two or more terms.

For example, the equation

\(x = 1 - (ay + b)(cx - d)\)

contains three terms, x, 1, and (ay + b)(cx - d).

In this book, you will often be asked to solve an equation. i.e. find out the value of an unknown quantity denoted by a symbol (for example ‘x’ or ‘y’).

The following table includes some mathematical symbols commonly used in physics for writing and solving equations. You may not be familiar with them all – check to make sure you know how they are all used.

Table M-1: Mathematical Symbols
\(=\)	is equal to
\(\neq\)	is not equal to
\(\approx\)	is approximately equal to
\(\sim\)	is of the order of
\(\propto\)	is proportional to
\(>\)	is greater than
\(\geq\)	is greater than or equal to
\(\gg\)	is much greater than
\(<\)	is less than
\(\leq\)	is less than or equal to
\(\ll\)	is much less than
\(\Delta x\)	change in x
\(\lvert x\rvert\)	absolute value of x
\(n!\)	\(n(n-1)(n-2)...1\)
\(\Sigma\)	sum

Table

Introduction to Equations (continued)

Throughout College Physics, you will see many examples of equations presented like this,

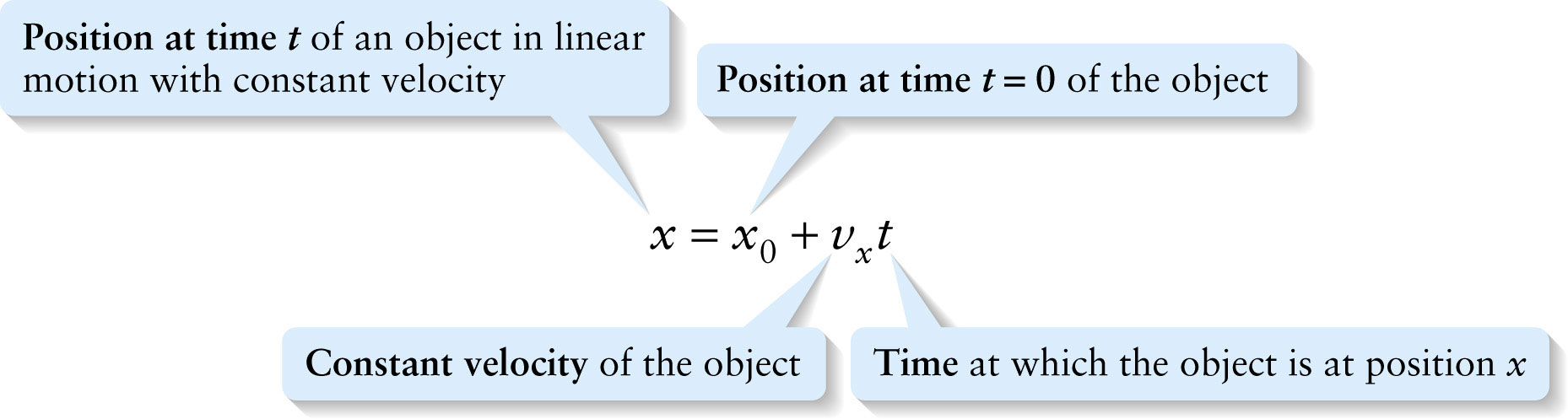
The balloons help you relate the parts of the equation to the physics, by describing how to match the correct numbers to each term.

Solving equations

Rearranging and manipulating the terms in an equation correctly is an important skill in physics. The quantities on each side of the equals sign can be operated on to solve the equation for an unknown quantity.

You can perform the following operations on equations:

The same quantity can be added to or subtracted from each side of an equation.
Each side of an equation can be multiplied or divided by the same quantity.
Each side of an equation can be raised to the same power.

To solve an equation you are likely to need to carry out more than one of these operations. These operations are meant to be applied to each side of the equation rather than each term in the equation. (Because multiplication is distributive over addition, operation 2—and only operation 2—of the preceding operations also applies term by term.)

Remember – never try to divide either side of an equation by zero! This will give you an invalid result.

Worked Example: Solving equations with addition and subtraction

Note: The same quantity can be added to or subtracted from each side of an equation.

Q. Find x when \(x – 3 = 7\),

A. Add 3 to both sides of the equation to give: \(x – 3 + 3 = 7 + 3\)

Therefore if we simplify what we have written,

\(x = 7 + 3\)

\(x = 10\)

IMPORTANT – don’t try to solve equations in your head – write down each step you take on paper. You might think the example above is easy but when things get more complicated a carefully written solution will be essential.

Worked Example: Solving equations with multiplication and division

Note: Each side of an equation can be multiplied or divided by the same quantity.

Q. Solve for x if \(3x = 17\)

A. Divide both sides of the equation by 3 to give

\(\frac{3x}{3}+\frac{17}{3}\)

\(x = \frac{17}{3}\)

Therefore,

\(x = 5.7\)

Worked Example: Solving equations with powers

Note: Each side of an equation can be raised to the same power.

Q. Take the equation, \(x^2 + 2 = 27\) and solve for x.

A. This problem will need two different steps to find the solution. First use the addition/subtraction rule from example 1 to get the x² term on its own on one side of the equation.

Subtract 2 from both sides,

\(x^2 + 2 – 2 = 27 – 2\), so

\(x^2 = 27 – 2\)

\(x^2 = 25\)

Now raise each side to the power ½ (note this is the same as taking the square root of both sides)

(x²)^{\(\frac{1}{2}\)} = (25)^{\(\frac{1}{2}\)}

Simplifying, \(x = 5\)

P’Cast M-2: Simplifying Reciprocals in an Equation

Try it yourself - practice solving equations

Try again.

Incorrect.