Chapter 1. Direct and inverse proportions

3.1 Introducing proportionality

Often quantities found in equations can be related to each other in a straightforward way. We can write simple relationships between these quantities to make solving problems a little easier.

For example, take the equation for average velocity,

The average velocity is calculated as the distance travelled, d divided by the time taken, t.

If the time taken is kept fixed, but I travel at a higher velocity, I will travel further (d is greater).

Notice that for a constant time interval, if I double V (travel twice as fast), the distance travelled will also double. We can say that the velocity is directly proportional to the distance travelled.

General Rules:

When we say variable quantities x and y are directly proportional, we mean that as x and y change, the ratio x/y is constant. To say that two quantities are proportional is to say that they are directly proportional. When we say variable quantities x and y are inversely proportional, we mean that as x and y change, the ratio xy is constant.

Relationships of direct and inverse proportion are common in physics.

Examples

• Objects moving at the same velocity v, have momenta p, directly proportional to their masses m. (p=mv).
• The ideal gas law (PV = nRT) states that pressure P is directly proportional to (absolute) temperature T, when volume V remains constant, and is inversely proportional to volume, when temperature remains constant.
• Ohm’s law (V = IR) states that the voltage V across a resistor is directly proportional to the electric current in the resistor when the resistance remains constant.

Try it Yourself 1

Test your understanding with these true/false questions

3.2 Constants of proportionality

When two quantities are directly proportional, the two quantities are related by a constant of proportionality.
For example - If you are paid for working at a regular rate R in dollars per day, the money M you earn is directly proportional to the time, t you work.

• The rate R is the constant of proportionality that relates the money earned in dollars to the time worked t in days:
• You can write this relationship as an equation, M = Rt (Money earned = earning rate x time worked).
• If you earn $400 in 5 days, the value of R is $400(5 days) = $80/day.

Sometimes the constant of proportionality can be ignored in proportion problems. Because the amount you earn in 8 days is 8/5 times what you earn in 5 days, this amount is

m8 days = 8days($400/5days) = $640

We will look at this idea more in the following section.

3.3 Writing proportionality relationships

In the simple equation, x = zy

If z is a constant, x is directly proportional to y.

This relationship can be written as

$x \propto y$

If two quantities are directly proportional then calculating x/y will always comes out as the same value - provided there are no other non-constant variables in the equation.

This means we can write another relationship

x₀/y₀ = x₁/y₁

The following worked example will demonstrate how this can be useful.

Worked Example: Stretching a spring (Hooke’s law)

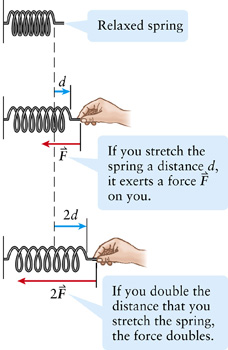
If you stretch a spring a distance d, it exerts a restoring force F on your hand. The force depends on how much you stretch the spring and this relationship is described by the equation,

F=-kd

• The force, F is directly proportional to the distance, d.
• This relationship can also be written as $F \propto d$
• -k is the constant of proportionality

Question: If the spring is initially stretched by 2cm from its relaxed position, I measure a restoring force of 10N. Calculate what the restoring force would be if I instead stretched the spring by 6cm from its rest position.

Solution: To solve this problem you could first solve for k using d = 2cm and F = 10N, and then use the value to find the value of F for d = 6cm, but we will do it a different way.

Since

F = -kd and –k is a constant, $F \propto d$

This means I can use the rule, F/d is a constant

We can write a new expression

F₀/d₀ = F₁/d₁

Where F₀ and d₀ represent the numerical values for the initial stretch and F₁ and d₁ represent the values for the second stretch.

Rearranging this expression gives,

F₁ = F₀d₁/d₀

Now you can solve for F₁

F₁ = 10N(6cm)/2cm = 30N

Notice that using this method we did not calculate a value for k, it was not needed to solve the problem.

Try it Yourself 2

Accelerating motion can be described by the equation F = ma where an acceleration, a results from an applied force, F on an object of mass m.

P’Cast: Painting Cubes

Try it Yourself 3