Chapter 1. Quadratic equations

Introduction to quadratic equations

Very generally, a quadratic equation is an equation of the form

where x and y are variables and and a, b, c, e, f, and g are constants. In each term of the equation the powers of the variables are integers equal to 2, 1, or 0.

This definition seems complicated, but if some of the terms are equal to zero, it can be a lot simpler.

Here are some examples of some different shorter quadratic equations – can you match their terms to those in the equation above?

3x² + 2y = 3

x² – xy –y = 0

y² –y = -1

A common factor in these equations is that at least one term is “squared”

Our first definition of a quadratic equation represents a general case but the designation quadratic equation often applies to a much simpler equation of one variable that can be written in the standard form.

where a, b, and c are constants.

The quadratic equation has two solutions or roots—values of x for which the equation is true. It can be important in physics to be able to find those solutions.

Solving quadratic equations

Quadratic equations have a parabolic shape when plotted on a graph as you can see here.

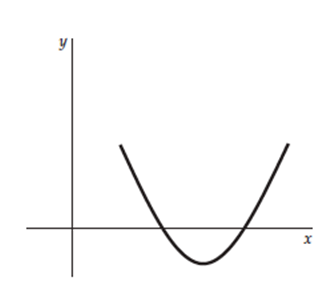
The equation of this line is quadratic:

An important thing to notice is that when y = 0

the curve intercepts the x axis

The values of x, where y = 0 are the solutions or roots of this quadratic equation.

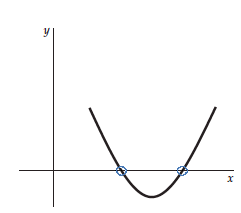
Solving quadratic equations – Factoring

Now we know that to solve a quadratic equation, we need to find the values of x, for which y = 0

When you multiply, divide, add, or subtract numbers, you must consider the accuracy of the results. Listed below are some rules that will help you determine the number of significant digits of your results.

We can solve some quadratic equations by factoring. Very often terms of an equation can be grouped or organized into other terms. When we factor terms, we look for multipliers and multiplicands—which we now call factors—that will yield two or more new terms as a product.

Factoring is useful for simplifying equations and for understanding the relationships between quantities. You should be familiar with the multiplication of the factors

(ax + by)(cx + dy) = acx² + (ad + bc)xy + bdy².

You should also practice recognizing some typical factorable combinations, these rules will help you to see the roots of a quadratic equation quickly.

1. Common factor: 2ax + 3ay = a(2x + 3y)

In this example there is an “a” in both terms, so can be factored out.

2. Perfect square: x² - 2xy + y² = (x-y)(x-y) = (x-y)²

This expression on the left side of this equation is a perfect square, the equation can be factored as shown and the two roots will be equal.

3. Difference of squares: x2 - y2 = (x + y)(x - y)

The equation on the left can be rewritten by factoring as shown above.

Worked example 1 – Factoring quadratic equations

Find the roots of the quadratic equation x2 - 3x + 2 = 0

This equation can be rearranged by factoring,

Factor the left side to get (x - 2)(x - 1) = 0.

Now we can see that only two values of x will satisfy the equation

If x = 2, then (x-2) = 0,

And

If x = 1, then (x-1) = 0

The solutions or ‘roots’ of the equation are x = 2 and x = 1.

Other factoring tips for simplifying equations

Look for factors that are prime numbers (2, 5, 7, etc.) because these factors can help you simplify terms quickly.

For example, the equation 98x – 140 = 0 can be simplified because 98 and 140 share the common factor 2.

That is, 98x² – 140 = 0 becomes

2(49x - 70) = 0, so we have 49x² – 70 = 0.

This result can be further simplified because 49 and 70 share the common factor 7.

Thus, 49x² – 70 = 0 becomes

7(7x² - 10) = 0, so we have 7x – 10 = 0.

Try it yourself – 1 - Factoring quadratic equations

Common factor: Identify the common factor in these expressions and factor it out. Then click to see the answers.

Perfect square and Difference of squares: Simplify these equations

P’Cast – Factoring a second degree polynomial

Solving quadratic equations – The quadratic formula

Not all quadratic equations can be solved by factoring. However, any quadratic equation in the standard form ax² + bx + c = 0 can be solved by the quadratic formula,

This equation has two solutions, expressed by the ± sign and they correspond to the two points where the quadratic curve crosses the x axis. When b² is greater than 4ac, there are two solutions to this equation corresponding to the + and - signs, respectively.

This figure shows a graph of y versus x where y = ax² + bx + c. The curve, a parabola, crosses the x axis twice.

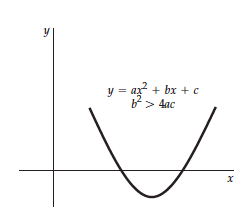
• When b² is less than 4ac

The graph of y versus x does not intersect the x axis, as shown in this graph. There are mathematically still two roots, but they are not real numbers.

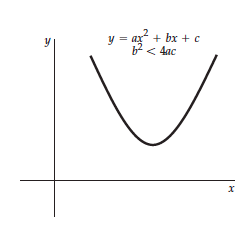
• When b²= 4ac

The graph of y versus x is tangent to the x axis at the point x = -b>2a; the two roots are each equal to -b>2a.

Can you sketch a graph to represent that situation?

Try it yourself – 2 - Solving quadratic equations with the quadratic formula

The quadratic formula is a very useful way to solve quadratic equations. It can be confusing to get all the terms right, but by practicing a few times you should get the hang of things.

Practice solving quadratic equations on these problems. Find the roots of each equation below.

Worked example – accelerated motion

We use and solve quadratic equations in solving problems in accelerated motion.

Question: I throw a ball straight up into the air with an initial velocity of 3m/s. My hand is 1.2m above the ground when I release the ball, calculate the time it takes for the ball to hit the ground after being released.

The motion of the ball can be represented by the equation

Where x is in the direction of motion and t is the time taken.

We can rewrite this equation using the numbers given in the problem and -9.81m/s² for the acceleration of the ball,

0 = 1.2 + 3t + 0.5(-9.81)t²

Notice I used x = 0 for the final position of the ball.

I can solve this equation for t using the quadratic formula.

Quadratic formula \(= \frac{-b \pm \sqrt{ b^{2}-4ac } }{2a}=- \frac{b}{2a} \pm \frac{1}{2a} \sqrt{ b^{2} -4ac}\)

In our equation, a = -4.905, b = 3 and c = 1.2

So the roots can be found at:

(-3+√(9-4(-4.905 x 1.2))/-9.81 = (-3+√32.544)/-9.81 = -0.28

And

(-3-√(9-4(-4.905 x 1.2))/-9.81 = (-3-√32.544)/-9.81 = 0.89

The positive result (0.89s) represents the time the ball takes to hit the ground.