Chapter 1. Trigonometry
8.1 Introduction - Trigonometry
What is trigonometry?
Trigonometry, which gets its name from Greek roots meaning “triangle” and “measure,” is the study of some important mathematical functions, called trigonometric functions.
These functions are most simply defined as ratios of the sides of right triangles. However, these right-triangle definitions are of limited use because they are valid only for angles between zero and 90°. However, the validity of the right-triangle definitions can be extended by defining the trigonometric functions in terms of the ratio of the coordinates of points on a circle of unit radius drawn centered at the origin of the xy plane.
In physics, we first encounter trigonometric functions when we use vectors to analyze motion in two dimensions. Trigonometric functions are also essential in the analysis of any kind of periodic behavior, such as circular motion, oscillatory motion, and wave mechanic so its really important that you become familiar with their use in physics problems.
8.2 Measuring Angles – Degrees and radians
The size of an angle formed by two intersecting straight lines is known as its “measure”.
The standard way of finding the measure of an angle is to place the angle so that its vertex, or point of intersection of the two lines that form the angle, is at the center of a circle located at the origin of a graph that has Cartesian coordinates and one of the lines extends rightward on the positive x axis.
- The distance traveled counterclockwise on the circumference from the positive x axis to reach the intersection of the circumference with the other line defines the measure of the angle (as shown by the arrow).
- Traveling clockwise to the second line would simply give us a negative measure; to illustrate basic concepts, we position the angle so that the smaller rotation will be in the counterclockwise direction.
Measuring angles in Degrees
One of the most familiar units for expressing the measure of an angle is the degree, which equals 1/360 of the full distance around the circumference of the circle.
For greater precision, or for smaller angles, we can either show degrees plus minutes (‘) and seconds (‘’),
One minute, 1’ = 1°/60
One second, 1’’ = 1’>60 = 1°/3600;
or show degrees as an ordinary decimal number.
Measuring angles in Radians
For scientific work, a more useful measure of an angle is the radian (rad). Again, place the angle with its vertex at the center of a circle and measure counterclockwise rotation around the circumference.
The measure of the angle in radians is then defined as the length of the circular arc from one line to the other divided by the radius of the circle. If s is the arc length and r is the radius of the circle, the angle θ measured in radians is
θ=s/r

Because the angle measured in radians is the ratio of two lengths (s and r), it is dimensionless.
You will often need to convert angles from degrees to radians or vice versa. The relation between radians and degrees is
360° = 2π radians Or 1 rad = 360°/2π = 57.3°
Try it yourself 1 - Test your knowledge of degrees and radians,
Try the following multiple choice questions on measuring angles.
Question Sequence
Question 1.
How many minutes make up a degree?
| A. |
| B. |
| C. |
| D. |
8.3 The trigonometric functions
The most well known trigonometric functions are Sine, Cosine and tangent. In the picture below we can see a right triangle formed by drawing the line segment BC perpendicular to AC. The lengths of the sides are labeled a, b, and c. Using this right angle triangle we can define the trigonometric functions sin θ (the sine), cos θ (the cosine), and tan θ (the tangent) for an acute angle θ.
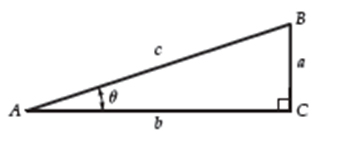
sinθ=ac=oppositesidehypotenuse
cosθ=bc=adjacentsidehypotenuse
tanθ=ab=oppositesideadjacentside=sinθcosθ
NOTE: Acute angles are angles whose positive rotation around the circumference of a circle measures less than 90° or π/2 radians.
8.4 More trigonometric functions
We can define three more trigonometric functions – they are the reciprocals of Sin, cos and tan, the secant (sec), the cosecant (csc) and the cotangent (cot).
cscθ=ca=1sinθ
secθ=cb=1cosθ
cotθ=ba=1tanθ=cosθsinθ
Finally we define the inverse trigonometric functions, by taking the inverse of sin, cos and tan to get arcsin, arccos and arctan.
If sin θ = x, then θ = arcsin x = sin-1x
If cos θ = y, then θ = arcos y = cos-1θ
If tan θ = z, the θ = arctan z = tan-1 z
Try it yourself 2 – The trigonometric functions
When you calculate trigonometric functions make sure that your calculator is in the correct angle mode (deg or rad).
Question 5.
sin 30
Question 6.
tan 45
Question 7.
cos 0
Question 8.
arcos 0
Question 9.
cot 20
Question 10.
sec 45
Question 11.
arctan 1.732
Now calculate the following for angle measured in radians.
Question 12.
sin π
Question 13.
tan (π/4)
Question 14.
csc (2π)
8.5 - Useful relations for angles
You can use the following geometric relationships between angles to help simplify physics problems
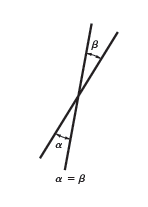
Rule 1 – When two straight lines cross, the opposite angles are equal.
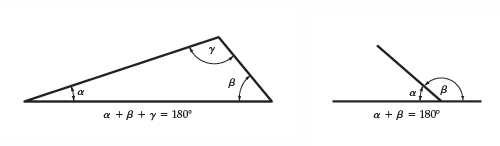
Rule 2 – The angles inside a triangle or around a horizontal line add up to 180°
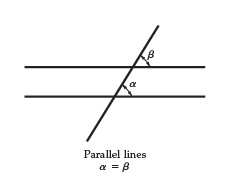
Rule 3 - When a line crosses two parallel lines, the corresponding angles are equal.
Two more useful geometric relationships.
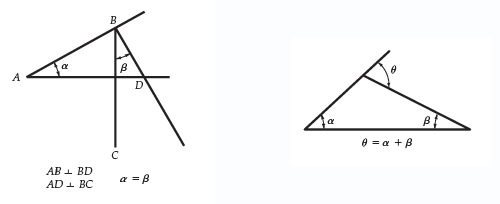
8.6 The trigonometric identities
We can derive several useful formulas, called trigonometric identities, by examining relationships between the trigonometric functions.
First we can start with the Pythagorean theorem
a2 + b2 = c2

Rearranging we get
a2c2+b2c2=1
Which if you recall the definitions of the trigonometric functions, can be written as,
sin2θ+cos2θ=1
Dividing the Pythagorean Theorem by a2 or b2 instead, gives us the formulae
1+cot2θ=csc2θ
1+tan2θ=sec2θ
There are in fact many more relationships between the trigonometric functions that can be derived from simple geometric relationships and are extremely useful. The table below and included in the book lists these last three and many more trigonometric identities.
{Insert table M-2 here.}
{Also insert example M-9 from the book here.}
8.7 – Some important examples of the trigonometric functions
1. The isosceles right angle triangle
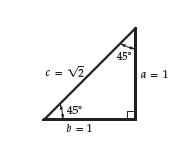
If we assume that the equal sides of this triangle have a length of one, then by the Pythagorean Theorem, the hypotenuse must be equal to
c=√a2+b2=√12+12=√2 units
This means we can calculate the trigonometric functions for 45° as
\mathtt{sin}{\,}45°=\frac{a}{c}=\frac{1}{\sqrt{2}}= 0.707 \quad \mathtt{cos}{\,}45°=\frac{b}{c}=\frac{1}{\sqrt{2}}= 0.707 \quad \mathtt{tan}{\,}45°=\frac{a}{b}=\frac{1}{1}=1
2. The 30-60-90 triangle
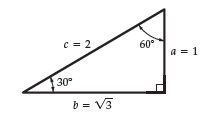
This triangle is half of an equilateral triangle with sides of lengths 1, 2 and √3.
Using this diagram you can see that the following equations must be true.
\mathtt{cos}{\,}30°=\frac{b}{c}=\frac{\sqrt{3}}{2}= 0.866 \quad \quad \quad \quad \mathtt{tan}{\,}30°=\frac{a}{b}=\frac{1}{\sqrt{3}}= 0.577
\mathtt{sin}{\,}60°=\frac{b}{c}=\mathtt{cos}{\,}30°= 0.866 \quad \quad \, \mathtt{cos}{\,}60°=\frac{a}{c}=\mathtt{sin}{\,}30°=\frac{1}{2}
\mathtt{tan}{\,}60°=\frac{b}{a}=\frac{\sqrt{3}}{1}= 1.732
8.8 – The small angle approximation
The diagram shows a right angle triangle and for small angles. Look a the diagram and you will see that the length, a is nearly equal to the arc length, s.
This means that the angle θ = s/c is therefore nearly equal to sin θ = a.
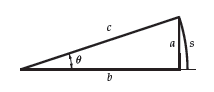
Using this idea we can say that for small angles
- sin θ ≈ θ
- tan θ ≈ sin θ ≈ θ
- cos θ ≈ 1
This graph shows graphs of θ, sin θ, and tan θ versus θ for small values of θ and shows how accurate the small angle approximations are.
If accuracy of a few percent is needed, small-angle approximations can be used only for angles of about a quarter of a radian (or about 15°) or less. Below this value, as the angle becomes smaller, the approximation tan θ ≈ sin θ ≈ θ is even more accurate.

For small angles:
tan θ ≈ sin θ ≈ θ
8.9 - Trigonometric functions as functions of real numbers
So far we have illustrated the trigonometric functions as properties of angles less than 90° (acute angles).
If we look at an angle larger than 90° (an obtuse angle), the trigonometric functions are described as:
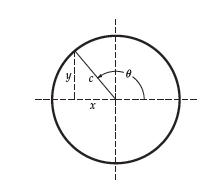
\mathtt{sin}{\,}\theta=\frac{y}{c}
\mathtt{cos}{\,}\theta=\frac{x}{c}
\mathtt{tan}{\,}\theta=\frac{y}{x}
What about negative signs?
You can find the sin, cos or tan of any angle as long as you remember that values of x to the left of the vertical axis and values of y below the horizontal axis are negative; c in the figure is always regarded as positive.
In the graphs below you can see the trigonometric functions, sin θ, cos θ and tan θ plotted as a function of angle θ.
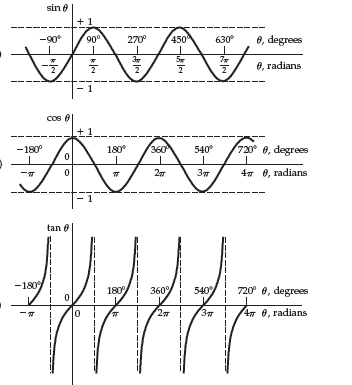
Notice how each function repeats itself.
The sin and cos functions repeat every 2\pi radians (or 360°), so
\quad\quad \mathtt{sin}{\,}(\theta + 2\pi)=\mathtt{sin}{\,}\theta
\quad\quad \mathtt{cos}{\,}(\theta + 2\pi)=\mathtt{cos}{\,}\theta
The tan function repeats every \pi radians (or 180°), so
\quad\quad \mathtt{tan}{\,}(\theta + 2\pi)=\mathtt{tan}{\,}\theta