25.1 Genotypic and Allelic Frequencies Are Used to Describe the Gene Pool of a Population
An obvious and pervasive feature of life is variability. Students in a typical college class will vary in eye color, hair color, skin pigmentation, height, weight, facial features, blood type, and susceptibility to numerous diseases and disorders. No two students in the class are likely to be the same in appearance.
Humans are not unique in their extensive variability (Figure 25.1a); almost all organisms exhibit variation in phenotype. For instance, lady beetles are highly variable in their spotting patterns (Figure 25.1b), mice vary in body size, snails have different numbers of stripes on their shells, and plants vary in their susceptibility to pests. Much of this phenotypic variation is hereditary. Recognition of the extent of phenotypic variation led Charles Darwin to the idea of evolution through natural selection. Genetic variation is the basis of all evolution, and the extent of genetic variation within a population affects its potential to adapt to environmental change.

In fact, even more genetic variation exists in populations than is visible in the phenotype. Much variation exists at the molecular level owing, in part, to the redundancy of the genetic code, which allows different codons to specify the same amino acid. Thus, two members of a population can produce the same protein even if their DNA sequences are different. DNA sequences between the genes and introns within genes do not encode proteins; much of the variation in these sequences also has little effect on the phenotype.
An important but frequently misunderstood tool used in population genetics is the mathematical model. Let’s take a moment to consider what a model is and how it can be used. A mathematical model usually describes a process as an equation. Factors that may influence the process are represented by variables in the equation; the equation defines the way in which the variables influence the process. Most models are simplified representations of a process, because the simultaneous consideration of all of the influencing factors is impossible; some factors must be ignored in order to examine the effects of others. At first, a model might consider only one or a few factors but, after their effects are understood, the model can be improved by the addition of more details. Importantly, even a simple model can be a source of valuable insight into how a process is influenced by key variables.
717
Before we can explore the evolutionary processes that shape genetic variation, we must be able to describe the genetic structure of a population. The usual way of describing this structure is to enumerate the types and frequencies of genotypes and alleles in a population.
Calculating Genotypic Frequencies
A frequency is simply a proportion or a percentage, usually expressed as a decimal fraction. For example, if 20% of the alleles at a particular locus in a population are A, we would say that the frequency of the A allele in the population is 0.20. For large populations, for which a determination of the genes of all individual members is impractical, a sample of the population is usually taken and the genotypic and allelic frequencies are calculated for this sample (see Chapter 24). The genotypic and allelic frequencies of the sample are then used to represent the gene pool of the population.
To calculate a genotypic frequency, we simply add up the number of individuals possessing the genotype and divide by the total number of individuals in the sample (N). For a locus with three genotypes AA, Aa, and aa, the frequency (f) of each genotype is

The sum of all the genotypic frequencies always equals 1.
Calculating Allelic Frequencies
The gene pool of a population can also be described in terms of the allelic frequencies. There are always fewer alleles than genotypes, so the gene pool of a population can be described in fewer terms when the allelic frequencies are used. In a sexually reproducing population, the genotypes are only temporary assemblages of the alleles. As described by Mendel’s principle of segregation, the genotypes break down each generation and individual alleles are passed to the next generation through the gametes. Thus, the types and numbers of alleles, rather than genotypes, have real continuity from one generation to the next and make up the gene pool of a population.
Allelic frequencies can be calculated from (1) the numbers or (2) the frequencies of the genotypes. To calculate the allelic frequency from the numbers of genotypes, we count the number of copies of a particular allele present in a sample and divide by the total number of all alleles in the sample:
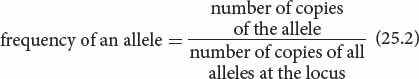
For a locus with only two alleles (A and a), the frequencies of the alleles are usually represented by the symbols p and q and can be calculated as follows:
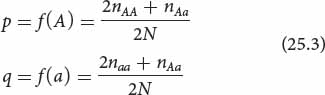
where nAA, nAa, and naa represent the numbers of AA, Aa, and aa individuals, and N represents the total number of individuals in the sample. To obtain the number of copies of the allele in the numerator of the equation, we add twice the number of homozygotes (because each has two copies of the allele for which the frequency is being calculated) to the number of heterozygotes (because each has a single copy of the allele). We divide by 2N because each diploid individual has two alleles at a locus. The sum of the allelic frequencies always equals 1 (p + q = 1); so, after p has been obtained, q can be determined by subtraction: q = 1 − p.
Alternatively, allelic frequencies can be calculated from the genotypic frequencies. This is useful if the genotypic frequencies have already been calculated and the numbers of the different genotypes are not available. To calculate an allelic frequency from genotypic frequencies, we add the frequency of the homozygote for each allele to half the frequency of the heterozygote (because half of the heterozygote’s alleles are of each type):
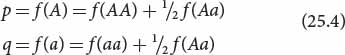
We obtain the same values of p and q whether we calculate the allelic frequencies from the numbers of genotypes (Equation 25.3) or from the genotypic frequencies (Equation 25.4). A sample calculation of allelic frequencies is provided in the next Worked Problem.  TRY PROBLEM 16
TRY PROBLEM 16
Loci with Multiple Alleles
We can use the same principles to determine the frequencies of alleles for loci with more than two alleles. To calculate the allelic frequencies from the numbers of genotypes, we count up the number of copies of an allele by adding twice the number of homozygotes to the number of heterozygotes that possess the allele and divide this sum by twice the number of individuals in the sample. For a locus with three alleles (A1, A2, and A3) and six genotypes (A1A1, A1A2, A2A2, A1A3, A2A3, and A3A3), the frequencies (p, q, and r) of the alleles are
718

Alternatively, we can calculate the frequencies of multiple alleles from the genotypic frequencies by extending Equation 25.4. Once again, we add the frequency of the homozygote to half the frequency of each heterozygous genotype that possesses the allele:
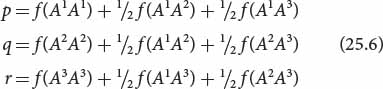
X-Linked Loci
To calculate allelic frequencies for genes at X-linked loci, we apply these same principles. However, we must remember that a female possesses two X chromosomes and therefore has two X-linked alleles, whereas a male has only a single X chromosome and one X-linked allele.
Suppose there are two alleles at an X-linked locus, XA and Xa. Females may be either homozygous (XAXA or XaXa) or heterozygous (XAXa). All males are hemizygous (XAY or XaY). To determine the frequency of the XA allele (p), we first count the number of copies of XA: we multiply the number of XAXA females by two and add the number of XAXa females and the number of XAY males. We then divide the sum by the total number of alleles at the locus, which is twice the total number of females plus the number of males:
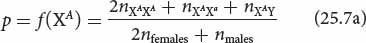
Similarly, the frequency of the Xa allele is
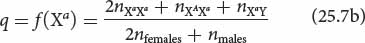
The frequencies of X-linked alleles can also be calculated from genotypic frequencies by adding the frequency of the females that are homozygous for the allele, half the frequency of the females that are heterozygous for the allele, and the frequency of males hemizygous for the allele:
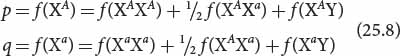
If you remember the logic behind these calculations, you can determine allelic frequencies for any set of genotypes, and it will not be necessary to memorize all of the formulas.  TRY PROBLEM 18
TRY PROBLEM 18
CONCEPTS
Population genetics concerns the genetic composition of a population and how it changes over time. The gene pool of a population can be described by the frequencies of genotypes and alleles in the population.
 CONCEPT CHECK 1
CONCEPT CHECK 1
What are some advantages of using allelic frequencies to describe the gene pool of a population instead of using genotypic frequencies?
WORKED PROBLEM
The human MN blood-type antigens are determined by two codominant alleles, LM and LN. The MN blood types and corresponding genotypes of 398 Finns from Karjala are tabulated here.
| Phenotype | Genotype | Number |
|---|---|---|
| MM | LMLM | 182 |
| MN | LMLN | 172 |
| NN | LNLN | 44 |
Source: W. C. Boyd, Genetics and the Races of Man (Boston: Little, Brown, 1950.)
Calculate the genotypic and allelic frequencies at the MN locus for the Karjala population.
Solution Strategy
What information is required in your answer to the problem?
The genotypic and allelic frequencies of the population.
What information is provided to solve the problem?
The numbers of the different MN genotypes in the sample.
Solution Steps
The genotypic frequencies for the population are calculated with the following formula:

719
The allelic frequencies can be calculated from either the numbers or the frequencies of the genotypes. To calculate allelic frequencies from numbers of genotypes, we add the number of copies of the allele and divide by the number of copies of all alleles at that locus.

To calculate the allelic frequencies from genotypic frequencies, we add the frequency of the homozygote for that genotype to half the frequency of each heterozygote possessing that allele:
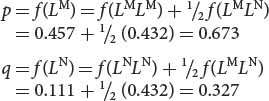
Now try your hand at calculating genotypic and allelic frequencies by working Problem 17 at the end of the chapter.