3.3 Dihybrid Crosses Reveal the Principle of Independent Assortment
We will now extend Mendel’s principle of segregation to more-complex crosses that include alleles at multiple loci. Understanding the nature of these crosses will require an additional principle, the principle of independent assortment.
Dihybrid Crosses
In addition to his work on monohybrid crosses, Mendel crossed varieties of peas that differed in two characteristics—a dihybrid cross. For example, he had one homozygous variety of pea with seeds that were round and yellow; another homozygous variety with seeds that were wrinkled and green. When he crossed the two varieties, the seeds of all the F1 progeny were round and yellow. He then self-fertilized the F1 and obtained the following progeny in the F2 : 315 round, yellow seeds; 101 wrinkled, yellow seeds; 108 round, green seeds; and 32 wrinkled, green seeds. Mendel recognized that these traits appeared approximately in a 9 : 3 : 3 : 1 ratio; that is,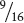 
of the progeny were round and yellow, 
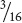were wrinkled and yellow,
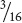were round and green, and 
were wrinkled and green.
The Principle of Independent Assortment
Mendel carried out a number of dihybrid crosses for pairs of characteristics and always obtained a 9 : 3 : 3 : 1 ratio in the F2. This ratio makes perfect sense in regard to segregation and dominance if we add a third principle, which Mendel recognized in his dihybrid crosses: the principle of independent assortment (Mendel’s second law). This principle states that alleles at different loci separate independently of one another (see Table 3.2).
A common mistake is to think that the principle of segregation and the principle of independent assortment refer to two different processes. The principle of independent assortment is really an extension of the principle of segregation. The principle of segregation states that the two alleles of a locus separate when gametes are formed; the principle of independent assortment states that, when these two alleles separate, their separation is independent of the separation of alleles at other loci.
Let’s see how the principle of independent assortment explains the results that Mendel obtained in his dihybrid cross. Each plant possesses two alleles encoding each characteristic, and so the parental plants must have had genotypes RR YY and rr yy (Figure 3.10a). The principle of segregation indicates that the alleles for each locus separate, and one allele for each locus passes to each gamete. The gametes produced by the round, yellow parent therefore contain alleles RY, whereas the gametes produced by the wrinkled, green parent contain alleles ry. These two types of gametes unite to produce the F1, all with genotype Rr Yy. Because round is dominant over wrinkled and yellow is dominant over green, the phenotype of the F1 will be round and yellow.
60
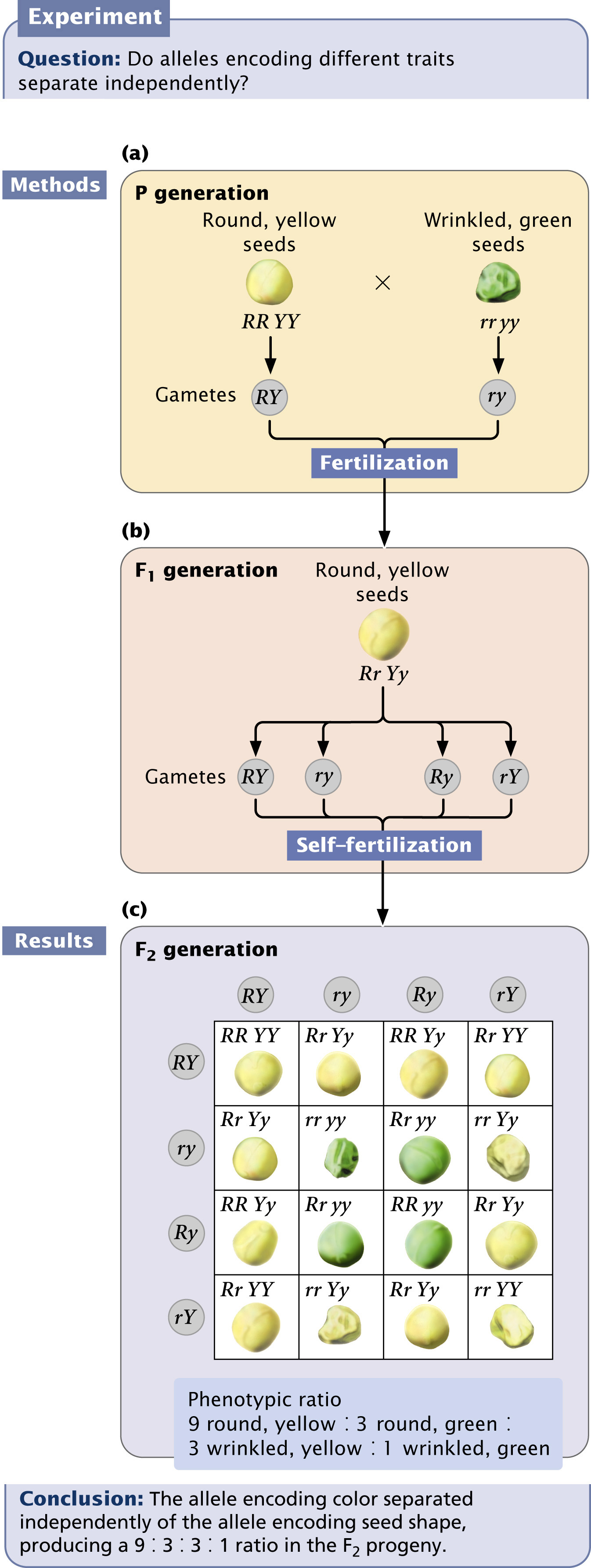
When Mendel self-fertilized the F1 plants to produce the F2, the alleles for each locus separated, with one allele going into each gamete. This event is where the principle of independent assortment becomes important. Each pair of alleles can separate in two ways: (1) R separates with Y, and r separates with y, to produce gametes RY and ry or (2) R separates with y, and r separates with Y, to produce gametes Ry and rY. The principle of independent assortment tells us that the alleles at each locus separate independently; thus, both kinds of separation take place equally and all four types of gametes (RY, ry, Ry, and rY) are produced in equal proportions (Figure 3.10b). When these four types of gametes are combined to produce the F2 generation, the progeny consist of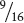
round and yellow,
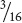wrinkled and yellow,
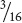round and green, and
wrinkled and green, resulting in a 9 : 3 : 3 : 1 phenotypic ratio (Figure 3.10c).
Relating the Principle of Independent Assortment to Meiosis
An important qualification of the principle of independent assortment is that it applies to characteristics encoded by loci located on different chromosomes because, like the principle of segregation, it is based wholly on the behavior of chromosomes in meiosis. Each pair of homologous chromosomes separates independently of all other pairs in anaphase I of meiosis (Figure 3.11); so genes located on different pairs of homologs will assort independently. Genes that happen to be located on the same chromosome will travel together during anaphase I of meiosis and will arrive at the same destination—within the same gamete (unless crossing over takes place). However, genes located on the same chromosome do not assort independently (unless they are located sufficiently far apart that crossing over takes place in every meiotic division, as will be discussed fully in Chapter 7).
61
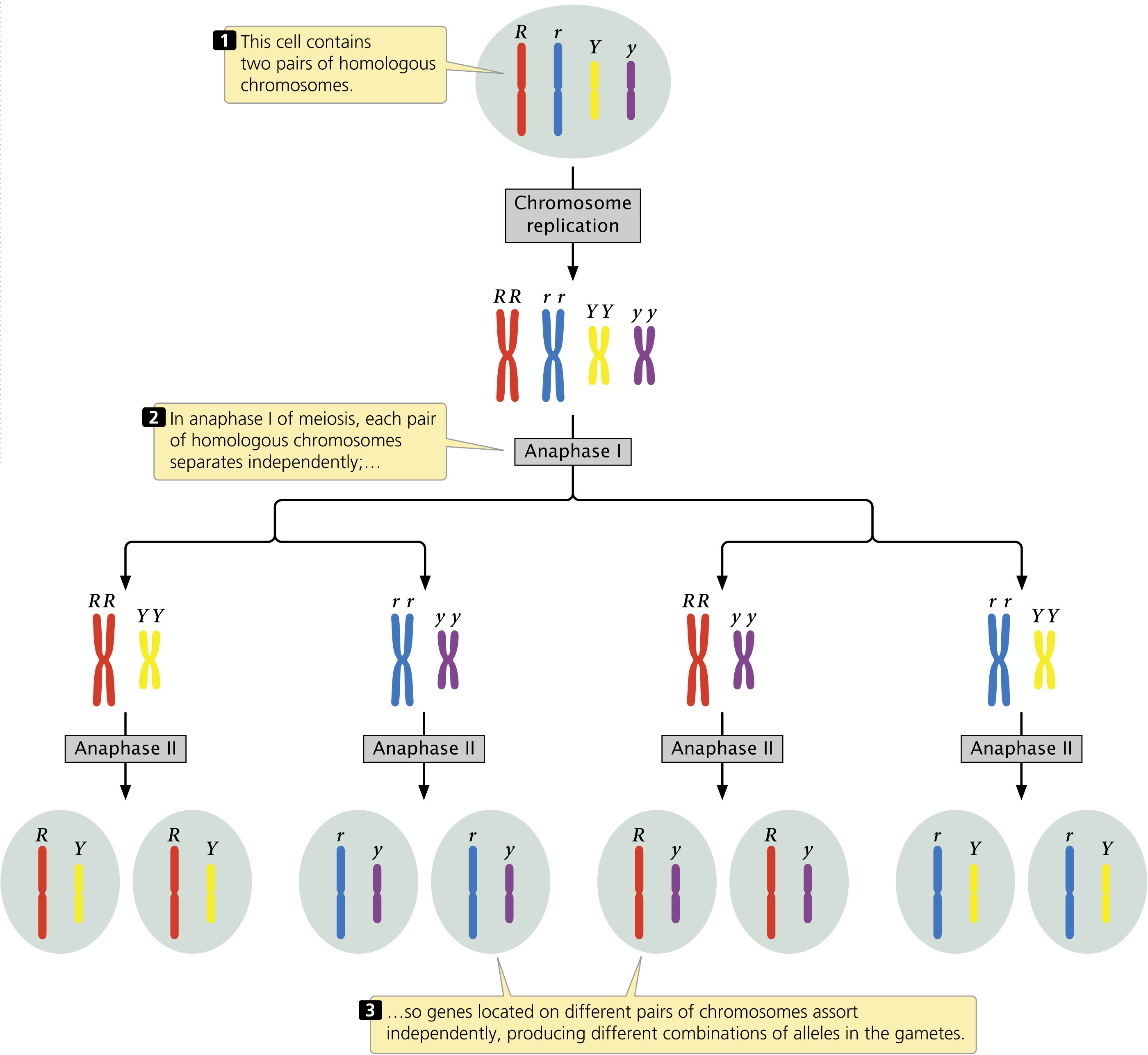
CONCEPTS
The principle of independent assortment states that genes encoding different characteristics separate independently of one another when gametes are formed, owing to the independent separation of homologous pairs of chromosomes in meiosis. Genes located close together on the same chromosome do not, however, assort independently.
CONCEPT CHECK 6
How are the principles of segregation and independent assortment related and how are they different?
Applying Probability and the Branch Diagram to Dihybrid Crosses
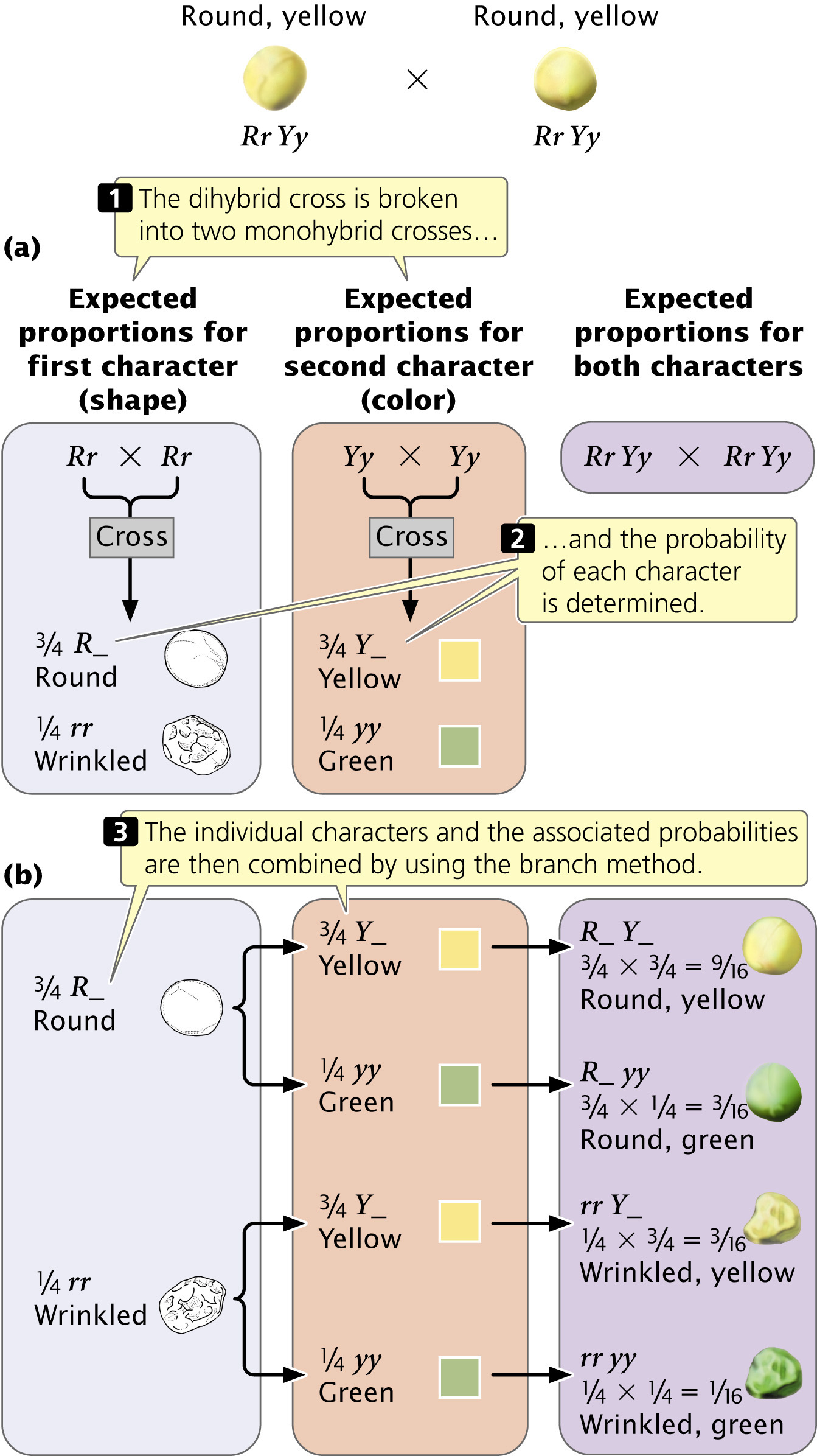
When the genes at two loci separate independently, a dihybrid cross can be understood as two monohybrid crosses. Let’s examine Mendel’s dihybrid cross (Rr Yy × Rr Yy) by considering each characteristic separately (Figure 3.12a). If we consider only the shape of the seeds, the cross was Rr × Rr, which yields a 3 : 1 phenotypic ratio (
round and 
wrinkled progeny, see Table 3.5). Next consider the other characteristic, the color of the seed. The cross was Yy × Yy, which produces a 3 : 1 phenotypic ratio (
yellow and
green progeny).
We can now combine these monohybrid ratios by using the multiplication rule to obtain the proportion of progeny with different combinations of seed shape and color. The proportion of progeny with round and yellow seeds is
(the probability of round) ×
(the probability of yellow) =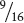
. The proportion of progeny with round and green seeds is
×
=
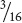; the proportion of progeny with wrinkled and yellow seeds is
×
=
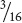; and the proportion of progeny with wrinkled and green seeds is
×
=
.
Branch diagrams are a convenient way of organizing all the combinations of characteristics (Figure 3.12b). In the first column, list the proportions of the phenotypes for one character (here,
round and
wrinkled). In the second column, list the proportions of the phenotypes for the second character (
yellow and
green) twice, next to each of the phenotypes in the first column: put
yellow and
green next to the round phenotype and again next to the wrinkled phenotype. Draw lines between the phenotypes in the first column and each of the phenotypes in the second column. Now follow each branch of the diagram, multiplying the probabilities for each trait along that branch. One branch leads from round to yellow, yielding round and yellow progeny. Another branch leads from round to green, yielding round and green progeny, and so forth. We calculate the probability of progeny with a particular combination of traits by using the multiplication rule: the probability of round (
) and yellow (
) seeds is
×
=
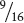. The advantage of the branch diagram is that it helps keep track of all the potential combinations of traits that may appear in the progeny. It can be used to determine phenotypic or genotypic ratios for any number of characteristics.
Using probability is much faster than using the Punnett square for crosses that include multiple loci. Genotypic and phenotypic ratios can be quickly worked out by combining, with the multiplication rule, the simple ratios in Tables 3.5 and 3.6. The probability method is particularly efficient if we need the probability of only a particular phenotype or genotype among the progeny of a cross. Suppose that we need to know the probability of obtaining the genotype Rr yy in the F2 of the dihybrid cross in Figure 3.10. The probability of obtaining the Rr genotype in a cross of Rr × Rr is 
and that of obtaining yy progeny in a cross of Yy × Yy is
(see Table 3.6). Using the multiplication rule, we find the probability of Rr yy to be
×
= 
.
62
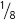To illustrate the advantage of the probability method, consider the cross Aa Bb cc Dd Ee × Aa Bb Cc dd Ee. Suppose that we want to know the probability of obtaining offspring with the genotype aa bb cc dd ee. If we use a Punnett square to determine this probability, we might be working on the solution for months. However, we can quickly figure the probability of obtaining this one genotype by breaking this cross into a series of single-locus crosses:
| Progeny cross | Genotype | Probability |
|---|---|---|
| Aa × Aa | aa |
|
| Bb × Bb | bb |
|
| cc × Cc | cc |
|
| Dd × dd | dd |
|
| Ee × Ee | ee |
|
The probability of an offspring from this cross having genotype aa bb cc dd ee is now easily obtained by using the multiplication rule:
×
×
×
×
= 
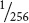. This calculation assumes that genes at these five loci all assort independently.
Now that you’ve had some experience working genetic crosses, explore Mendel’s principles of heredity by setting up some of your own crosses in 
Animation 3.1.
CONCEPTS
A cross including several characteristics can be worked by breaking the cross down into single-locus crosses and using the multiplication rule to determine the proportions of combinations of characteristics (provided that the genes assort independently).
The Dihybrid Testcross
Let’s practice using the branch diagram by determining the types and proportions of phenotypes in a dihybrid testcross between the round and yellow F1 plants (Rr Yy) obtained by Mendel in his dihybrid cross and the wrinkled and green plants (rr yy), as depicted in Figure 3.13. Break the cross down into a series of single-locus crosses. The cross Rr × rr yields
round (Rr) progeny and
wrinkled (rr) progeny. The cross Yy × yy yields
yellow (Yy) progeny and
green (yy) progeny. Using the multiplication rule, we find the proportion of round and yellow progeny to be
(the probability of round) ×
(the probability of yellow) =
. Four combinations of traits with the following proportions appear in the offspring:
Rr Yy, round yellow;
Rr yy, round green;
rr Yy, wrinkled yellow; and
rr yy, wrinkled green.
WORKED PROBLEM
The principles of segregation and independent assortment are important not only because they explain how heredity works, but also because they provide the means for predicting the outcome of genetic crosses. This predictive power has made genetics a powerful tool in agriculture and other fields, and the ability to apply the principles of heredity is an important skill for all students of genetics. Practice with genetic problems is essential for mastering the basic principles of heredity; no amount of reading and memorization can substitute for the experience gained by deriving solutions to specific problems in genetics.
You may find genetics problems difficult if you are unsure of where to begin or how to organize a solution to the problem. In genetics, every problem is different, so no common series of steps can be applied to all genetics problems. Logic and common sense must be used to analyze a problem and arrive at a solution. Nevertheless, certain steps can facilitate the process, and solving the following problem will serve to illustrate these steps.
63
In mice, black coat color (B) is dominant over brown (b), and a solid pattern (S) is dominant over white spotted (s). Color and spotting are controlled by genes that assort independently. A homozygous black, spotted mouse is crossed with a homozygous brown, solid mouse. All the F1 mice are black and solid. A testcross is then carried out by mating the F1 mice with brown, spotted mice.
- a. Give the genotypes of the parents and the F1 mice.
- b. Give the genotypes and phenotypes, along with their expected ratios, of the progeny expected from the testcross.
Solution Strategy
What information is required in your answer to the problem?
First, determine what question or questions the problem is asking. Is it asking for genotypes, genotypic ratios, or phenotypic ratios? This problem asks you to provide the genotypes of the parents and the F1, the expected genotypes and phenotypes of the progeny of the testcross, and their expected proportions.
What information is provided to solve the problem?
Next determine what information is provided that will be necessary to solve the problem. This problem gives important information about the dominance relations of the characters and the genes that code for the traits.
black is dominant over brown.-
solid is dominant over white spotted.
-
the genes for the two characteristics assort independently.
-
symbols for the different alleles: B for black, b for brown, S for solid, and s for spotted.
It is often helpful to write down the symbols at the beginning of the solution:
B—black
b—brown
S—solid
s—white spotted
Next, write out the crosses given in the problem.
For help with this problem, review:
If you need help solving the problem, review those sections of the chapter that cover the relevant information. For this problem, review Sections 3.2 and 3.3.
Solution Steps
STEP 1 Write down any genetic information that can be determined from the phenotypes alone.
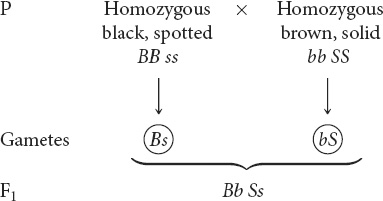
From the phenotypes and the statement that they are homozygous, you know that the P-generation mice must be BB ss and bb SS. The F1 mice are black and solid, both dominant traits, and so the F1 mice must possess at least one black allele (B) and one solid allele (S). At this point, you cannot be certain about the other alleles; so represent the genotype of the F1 as B_ S_, where _ means that any allele is possible. The brown, spotted mice in the testcross must be bb ss because both brown and spotted are recessive traits that will be expressed only if two recessive alleles are present. Record these genotypes on the crosses that you wrote out in step 2:
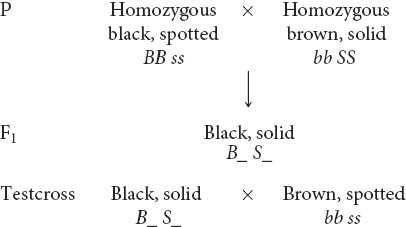
STEP 2 Break the problem down into smaller parts.
First, determine the genotype of the F1. After this genotype has been determined, you can predict the results of the testcross and determine the genotypes and phenotypes of the progeny from the testcross. Second, because this cross includes two independently assorting loci, it can be conveniently broken down into two single-locus crosses: one for coat color and the other for spotting. Third, use a branch diagram to determine the proportion of progeny of the testcross with different combinations of the two traits.
STEP 3 Work the different parts of the problem.
Start by determining the genotype of the F1 progeny. Mendel’s first law indicates that the two alleles at a locus separate, one going into each gamete. Thus, the gametes produced by the black, spotted parent contain B s and the gametes produced by the brown, solid parent contain b S, which combine to produce F1 progeny with the genotype Bb Ss:
64
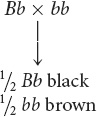
Use the F1 genotype to work the testcross (Bb Ss × bb ss), breaking it into two single-locus crosses. First, consider the cross for coat color: Bb × bb. Any cross between a heterozygote and a homozygous recessive genotype produces a 1 : 1 phenotypic ratio of progeny (see Table 3.5):
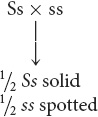
Next, do the cross for spotting: Ss × ss. This cross also is between a heterozygote and a homozygous recessive genotype and will produce
solid (Ss) and
spotted (ss) progeny (see Table 3.5).
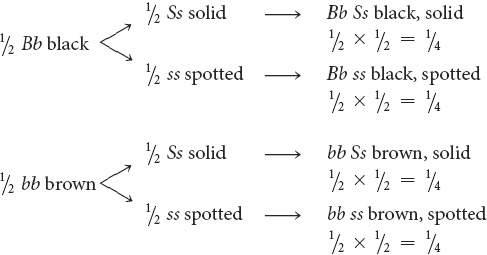
Finally, determine the proportions of progeny with combinations of these characters by using the branch diagram.
STEP 4 Check all work.
As a last step, reread the problem, checking to see if your answers are consistent with the information provided. You have used the genotypes BB ss and bb SS in the P generation. Do these genotypes encode the phenotypes given in the problem? Are the F1 progeny phenotypes consistent with the genotypes that you assigned? The answers are consistent with the information.
Now that we have stepped through a genetics problem together try your hand at Problem 33 at the end of this chapter.