Answers to Concept Checks
- 1. b
- 2. A locus is a place on a chromosome where genetic information encoding a characteristic is located. An allele is a version of a gene that encodes a specific trait. A genotype is the set of alleles possessed by an individual organism, and a phenotype is the manifestation or appearance of a characteristic.
- 3. Because the traits for both alleles appeared in the F2 progeny
- 4. d
- 5. a
- 6. Both the principle of segregation and the principle of independent assortment refer to the separation of alleles in anaphase I of meiosis. The principle of segregation says that these alleles separate, and the principle of independent assortment says that they separate independently of alleles at other loci.
- 7. d
WORKED PROBLEMS
Short hair (S) in rabbits is dominant over long hair (s). The following crosses are carried out, producing the progeny shown. Give all possible genotypes of the parents in each cross.
| Parents | Progeny | |
|---|---|---|
| a. | short × short | 4 short and 2 long |
| b. | short × short | 8 short |
| c. | short × long | 12 short |
| d. | short × long | 3 short and 1 long |
| e. | long × long | 2 long |
What information is required in your answer to the problem?
All possible genotypes of the parents in each cross.
What information is provided to solve the problem?
 Short hair is dominant over long hair.
Short hair is dominant over long hair. Phenotypes of the parents of each cross.
Phenotypes of the parents of each cross. Phenotypes and number of progeny of each cross.
Phenotypes and number of progeny of each cross.
For help with this problem, review:
Connecting Concepts: Ratios in Simple Crosses, in Section 3.2.
Solution Steps
For this problem, it is useful to first gather as much information about the genotypes of the parents as possible on the basis of their phenotypes. We can then look at the types of progeny produced to provide the missing information.
Note: The problem asks for all possible genotypes of the parents.
- a. short × short 4 short and 2 long
Because short hair is dominant over long hair, a rabbit having short hair could be either SS or Ss. The 2 long-haired offspring must be homozygous (ss) because long hair is recessive and will appear in the phenotype only when both alleles for long hair are present. Because each parent contributes one of the two alleles found in the progeny, each parent must be carrying the s allele and must therefore be Ss.Note: When both parents are heterozygotes (Ss × Ss) we expect to see a 3:1 ratio in progeny, but just by chance the progeny exhibited a 4 : 2 ratio.
- b. short × short 8 short
The short-haired parents could be SS or Ss. All eight of the offspring are short (S_), and so at least one of the parents is likely to be homozygous (SS); if both parents were heterozygous, we would expect of the progeny to be long haired (ss), but we do not observe any long-haired progeny. The other parent could be homozygous (SS) or heterozygous (Ss); as long as one parent is homozygous, all the offspring will be short haired. It is theoretically possible, although unlikely, that both parents are heterozygous (Ss × Ss). If both were heterozygous, we would expect two of the eight progeny to be long haired. Although no long-haired progeny are observed, it is possible that just by chance no long-haired rabbits would be produced among the eight progeny of the cross.
of the progeny to be long haired (ss), but we do not observe any long-haired progeny. The other parent could be homozygous (SS) or heterozygous (Ss); as long as one parent is homozygous, all the offspring will be short haired. It is theoretically possible, although unlikely, that both parents are heterozygous (Ss × Ss). If both were heterozygous, we would expect two of the eight progeny to be long haired. Although no long-haired progeny are observed, it is possible that just by chance no long-haired rabbits would be produced among the eight progeny of the cross. - c. short × long 12 short
The short-haired parent could be SS or Ss. The long-haired parent must be ss. If the short-haired parent were heterozygous (Ss), half of the offspring would be expected to be long haired, but we don’t see any long-haired progeny. Therefore, this parent is most likely homozygous (SS). It is theoretically possible, although unlikely, that the parent is heterozygous and just by chance no long-haired progeny were produced. - d. short × long 3 short and 1 long
On the basis of its phenotype, the short-haired parent could be homozygous (SS) or heterozygous (Ss), but the presence of one long-haired offspring tells us that the short-haired parent must be heterozygous (Ss). The long-haired parent must be homozygous (ss). - e. long × long 2 long
Because long hair is recessive, both parents must be homozygous for a long-hair allele (ss).
In cats, black coat color is dominant over gray. A female black cat whose mother is gray mates with a gray male. If this female has a litter of six kittens, what is the probability that three will be black and three will be gray?
Solution Strategy
What information is required in your answer to the problem?
The probability that in a litter of six kittens, three will be black and three will be gray.
What information is provided to solve the problem?
 Black is dominant to gray.
Black is dominant to gray. The mother of the litter is black and her mother is gray.
The mother of the litter is black and her mother is gray. The father of the litter is gray.
The father of the litter is gray.
For help with this problem, review:
The binomial expansion and probability, in Section 3.2.
Solution Steps
Because black (G) is dominant over gray (g), a black cat may be homozygous (GG) or heterozygous (Gg). The black female in this problem must be heterozygous (Gg) because her mother is gray (gg) and she must inherit one of her mother’s alleles. The gray male is homozygous (gg) because gray is recessive. Thus the cross is:
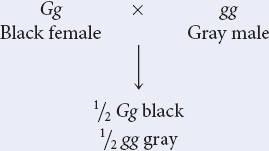
Hint: We can determine the female parent’s genotype from her phenotype and her mother’s phenotype.
We can use the binomial expansion to determine the probability of obtaining three black and three gray kittens in a litter of six. Let p equal the probability of a kitten being black and q equal the probability of a kitten being gray. The binomial is (p + q)6, the expansion of which is:
(p + q)6 = p6 + 6p5q + 15p4q2 + 20p3q3 + 15p2q4 + 6p1q5 + q6
Recall: The binomial expansion can be used to determine the probability of different combinations of traits in the progeny of a cross.
Hint: See pp. 56–57 for an explanation of how to expand the binomial.
The probability of obtaining three black and three gray kittens in a litter of six is provided by the term 20p3q3. The probabilities of p and q are both  ; so the overall probability is 20(
; so the overall probability is 20( )3(
)3( )3 =
)3 = 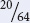 =
=  .
.
In corn, purple kernels are dominant over yellow kernels, and full kernels are dominant over shrunken kernels. A corn plant having purple and full kernels is crossed with a plant having yellow and shrunken kernels, and the following progeny are obtained:
| purple, full | 112 |
| purple, shrunken | 103 |
| yellow, full | 91 |
| yellow, shrunken | 94 |
What are the most likely genotypes of the parents and progeny? Test your genetic hypothesis with a chi-square test.
Solution Strategy
What information is required in your answer to the problem?
The genotypes of parents and progeny. A chi-square test comparing the observed and expected results.
What information is provided to help solve the problem?
 Purple kernels are dominant over yellow kernels and full kernels are dominant over shrunken kernels.
Purple kernels are dominant over yellow kernels and full kernels are dominant over shrunken kernels. The phenotypes of the parents.
The phenotypes of the parents. The phenotypes and numbers of the different progeny of the cross.
The phenotypes and numbers of the different progeny of the cross.
For help with this problem, review:
Sections 3.3 and 3.4.
Solution Steps
The best way to begin this problem is by breaking the cross down into simple crosses for a single characteristic (seed color or seed shape):
| P | purple × yellow | full × shrunken |
| F1 | 112 + 103 = 215 purple | 112 + 91 = 203 full |
| 91 + 94 = 185 yellow | 103 + 94 = 197 shrunken |
Hint: A good strategy in a cross involving multiple characteristics is to analyze the results for each characteristic separately.
In this cross, purple × yellow produces approximately  purple and
purple and  yellow (a 1 : 1 ratio). A 1 : 1 ratio is usually caused by a cross between a heterozygote and a homozygote. Because purple is dominant, the purple parent must be heterozygous (Pp) and the yellow parent must be homozygous (pp). The purple progeny produced by this cross will be heterozygous (Pp) and the yellow progeny must be homozygous (pp).
yellow (a 1 : 1 ratio). A 1 : 1 ratio is usually caused by a cross between a heterozygote and a homozygote. Because purple is dominant, the purple parent must be heterozygous (Pp) and the yellow parent must be homozygous (pp). The purple progeny produced by this cross will be heterozygous (Pp) and the yellow progeny must be homozygous (pp).
Now let’s examine the other character. Full × shrunken produces  full and
full and  shrunken, or a 1 : 1 ratio, so these progeny phenotypes are also produced by a cross between a heterozygote (Ff) and a homozygote (ff); the full-kernel progeny will be heterozygous (Ff) and the shrunken-kernel progeny will be homozygous (ff).
shrunken, or a 1 : 1 ratio, so these progeny phenotypes are also produced by a cross between a heterozygote (Ff) and a homozygote (ff); the full-kernel progeny will be heterozygous (Ff) and the shrunken-kernel progeny will be homozygous (ff).
Now combine the two crosses and use the multiplication rule to obtain the overall genotypes and the proportions of each genotype:
| P | Purple, full Pp Ff | × | Yellow, shrunken pp ff |
| F1 |
Pp Ff =  purple
purple |
× |
 full =
full =  purple, full
purple, full |
Pp ff =  purple
purple |
× |
 shrunken =
shrunken =  purple, shrunken
purple, shrunken |
|
Pp Ff =  yellow
yellow |
× |
 full =
full =  yellow, full
yellow, full |
|
Pp ff =  yellow
yellow |
× |
 shrunken =
shrunken =  yellow, shrunken
yellow, shrunken |
Recall: The multiplication rule states that the probability of two or more independent events occurring together is calculated by multiplying their independent probabilities.
Our genetic explanation predicts that, from this cross, we should see  purple, full-kernel progeny;
purple, full-kernel progeny;  purple, shrunken-kernel progeny;
purple, shrunken-kernel progeny;  yellow, full-kernel progeny; and
yellow, full-kernel progeny; and  yellow, shrunken-kernel progeny. A total of 400 progeny were produced; so
yellow, shrunken-kernel progeny. A total of 400 progeny were produced; so  × 400 = 100 of each phenotype are expected. These observed numbers do not fit the expected numbers exactly. Could the difference between what we observe and what we expect be due to chance? If the probability is high that chance alone is responsible for the difference between observed and expected, we will assume that the progeny have been produced in the 1 : 1 : 1 : 1 ratio predicted by the cross. If the probability that the difference between observed and expected is due to chance is low, the progeny are not really in the predicted ratio and some other, significant factor must be responsible for the deviation.
× 400 = 100 of each phenotype are expected. These observed numbers do not fit the expected numbers exactly. Could the difference between what we observe and what we expect be due to chance? If the probability is high that chance alone is responsible for the difference between observed and expected, we will assume that the progeny have been produced in the 1 : 1 : 1 : 1 ratio predicted by the cross. If the probability that the difference between observed and expected is due to chance is low, the progeny are not really in the predicted ratio and some other, significant factor must be responsible for the deviation.
The observed and expected numbers are:
| Phenotype | Observed | Expected |
|---|---|---|
| purple, full | 112 |
 × 400 = 100
× 400 = 100 |
| purple, shrunken | 103 |
 × 400 = 100
× 400 = 100 |
| yellow, full | 91 |
 × 400 = 100
× 400 = 100 |
| yellow, shrunken | 94 |
 × 400 = 100
× 400 = 100 |
To determine the probability that the difference between observed and expected is due to chance, we calculate a chi-square value with the formula χ2 = ∑[(observed − expected)2/expected]:
Hint: See Figure 3.14 for help on how to carry out a chi-square test.

Now that we have the chi-square value, we must determine the probability that this chi-square value is due to chance. To obtain this probability, we first calculate the degrees of freedom, which for a chi-square goodness-of-fit test are n − 1, where n equals the number of expected phenotypic classes. In this case, there are four expected phenotypic classes; so the degrees of freedom equal 4 − 1 = 3. We must now look up the chi-square value in a chi-square table (see Table 3.7). We select the row corresponding to 3 degrees of freedom and look along this row to find our calculated chi-square value. The calculated chi-square value of 2.7 lies between 2.366 (a probability of 0.5) and 6.251 (a probability of 0.1). The probability (P) associated with the calculated chi-square value is therefore 0.5 < P < 0.1. This is the probability that the difference between what we observed and what we expect is due to chance, which in this case is relatively high, and so chance is likely responsible for the deviation. We can conclude that the progeny do appear in the 1 : 1 : 1 : 1 ratio predicted by our genetic explanation.