5.2 Gene Interaction Takes Place When Genes at Multiple Loci Determine a Single Phenotype
In the dihybrid crosses that we examined in Chapter 3, each locus had an independent effect on the phenotype. When Mendel crossed a homozygous round and yellow plant (RR YY) with a homozygous wrinkled and green plant (rr yy) and then self-fertilized the F1, he obtained F2 progeny in the following proportions:
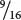 R_ Y_
R_ Y_ |
round, yellow |
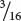 R_ yy
R_ yy
|
round, green |
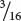 rr Y_
rr Y_ |
wrinkled, yellow |
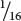 rr yy
rr yy
|
wrinkled, green |
In this example, the genes showed two kinds of independence. First, the genes at each locus are independent in their assortment in meiosis, which produced the 9 : 3 : 3 : 1 ratio of phenotypes in the progeny, in accord with Mendel’s principle of independent assortment. Second, the genes are independent in their phenotypic expression: the R and r alleles affect only the shape of the seed and have no influence on the color of the seed; the Y and y alleles affect only color and have no influence on the shape of the seed.
Frequently, genes exhibit independent assortment but do not act independently in their phenotypic expression; instead, the effects of genes at one locus depend on the presence of genes at other loci. This type of interaction between the effects of genes at different loci (genes that are not allelic) is termed gene interaction. With gene interaction, the products of genes at different loci combine to produce new phenotypes that are not predictable from the single-locus effects alone. In our consideration of gene interaction, we will focus primarily on interaction between the effects of genes at two loci, although interactions among genes at three, four, or more loci are common.
CONCEPTS
In gene interaction, genes at different loci contribute to the determination of a single phenotypic characteristic.
 CONCEPT CHECK 6
CONCEPT CHECK 6How does gene interaction differ from dominance between alleles?
Gene Interaction That Produces Novel Phenotypes
Let’s first examine gene interaction in which genes at two loci interact to produce a single characteristic. Fruit color in the pepper Capsicum annuum is determined in this way. Certain types of peppers produce fruits in one of four colors: red, peach, orange (sometimes called yellow), and cream (or white). If a homozygous plant with red peppers is crossed with a homozygous plant with cream peppers, all the F1 plants have red peppers (Figure 5.7a). When the F1 are crossed with each other, the F2 are in a ratio of 9 red : 3 : peach : 3 orange : 1 cream (Figure 5.7b). This dihybrid ratio (see Chapter 3) is produced by a cross between two plants that are both heterozygous for two loci (Y+y C+c × Y+y C+c). In this example, the Y locus and the C locus interact to produce a single phenotype—the color of the pepper:

| Genotype | Phenotype |
|---|---|
| Y+_ C +_ | red |
| Y+_ cc | peach |
| yy C+_ | orange |
| yy cc | cream |
Color in peppers of Capsicum annuum results from the relative amounts of red and yellow carotenoids, compounds that are synthesized in a complex biochemical pathway. The Y locus encodes one enzyme (the first step in the pathway), and the C locus encodes a different enzyme (the last step in the pathway). When different loci influence different steps in a common biochemical pathway, gene interaction often arises because the product of one enzyme affects the substrate of another enzyme.
To illustrate how Mendel’s rules of heredity can be used to understand the inheritance of characteristics determined by gene interaction, let’s consider a testcross between an F1 plant from the cross in Figure 5.7 (Y+y C+c) and a plant with cream peppers (yy cc). As outlined in Chapter 3 for independent loci, we can work this cross by breaking it down into two simple crosses. At the first locus, the heterozygote Y+y is crossed with the homozygote yy; this cross produces 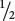 Y+y and
Y+y and 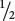 yy progeny. Similarly, at the second locus, the heterozygous genotype C+c is crossed with the homozygous genotype cc, producing
yy progeny. Similarly, at the second locus, the heterozygous genotype C+c is crossed with the homozygous genotype cc, producing 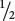 C+c and
C+c and 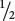 cc progeny. In accord with Mendel’s principle of independent assortment, these single-locus ratios can be combined by using the multiplication rule: the probability of obtaining the genotype Y+y C+c is the probability of Y+y (
cc progeny. In accord with Mendel’s principle of independent assortment, these single-locus ratios can be combined by using the multiplication rule: the probability of obtaining the genotype Y+y C+c is the probability of Y+y (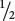 ) multiplied by the probability of C+c (
) multiplied by the probability of C+c (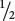 ), or
), or 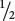 ×
× 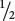 =
= 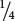 . The probability of each progeny genotype resulting from the testcross is:
. The probability of each progeny genotype resulting from the testcross is:
| Progeny genotype | Probability at each locus | Overall probability | Phenotype | |
|---|---|---|---|---|
| Y+y C+c |
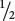 ×
×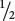
|
= |
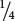
|
red peppers |
| Y+y cc |
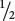 ×
×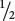
|
= |
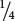
|
peach peppers |
| yy C+ c |
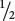 ×
× 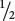
|
= |
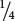
|
orange peppers |
| yy cc |
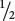 ×
× 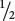
|
= |
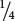
|
cream peppers |
When you work problems with gene interaction, it is especially important to determine the probabilities of single-locus genotypes and to multiply the probabilities of genotypes, not phenotypes, because the phenotypes cannot be determined without considering the effects of the genotypes at all the contributing loci.  TRY PROBLEM 25
TRY PROBLEM 25
Gene Interaction with EpistasisSometimes the effect of gene interaction is that one gene masks (hides) the effect of another gene at a different locus, a phenomenon known as epistasis. In the examples of genic interaction that we have examined, genes at different loci interact to determine a single phenotype. In those examples, one gene did not mask the effect of a gene at another locus, meaning that there was no epistasis. Epistasis is similar to dominance, except that dominance entails the masking of genes at the same locus (allelic genes). In epistasis, the gene that does the masking is called an epistatic gene; the gene whose effect is masked is a hypostatic gene. Epistatic genes may be recessive or dominant in their effects.
Recessive Epistasis
Recessive epistasis is seen in the genes that determine coat color in Labrador retrievers. These dogs may be black, brown (frequently called chocolate), or yellow; their different coat colors are determined by interactions between genes at two loci (although a number of other loci also help to determine coat color). One locus determines the type of pigment produced by the skin cells: a dominant allele B encodes black pigment, whereas a recessive allele b encodes brown pigment. Alleles at a second locus affect the deposition of the pigment in the shaft of the hair; dominant allele E allows dark pigment (black or brown) to be deposited, whereas recessive allele e prevents the deposition of dark pigment, causing the hair to be yellow. The presence of genotype ee at the second locus therefore masks the expression of the black and brown alleles at the first locus. The genotypes that determine coat color and their phenotypes are:
| Genotype | Phenotype |
|---|---|
| B_ E_ | black |
| bb E_ | brown |
| B_ ee | yellow |
| bb ee | yellow |
If we cross a black Labrador homozygous for the dominant alleles (BB EE) with a yellow Labrador homozygous for the recessive alleles (bb ee) and then intercross the F1, we obtain progeny in the F2 in a 9 : 3 : 4 ratio:

Notice that yellow dogs can carry alleles for either black or brown pigment, but these alleles are not expressed in their coat color.
In this example of gene interaction, allele e is epistatic to B and b, because e masks the expression of the alleles for black and brown pigments, and alleles B and b are hypostatic to e. In this case, e is a recessive epistatic allele, because two copies of e must be present to mask the expression of the black and brown pigments.  TRY PROBLEM 29
TRY PROBLEM 29
Another example of a recessive epistatic gene is the gene that determines the Bombay phenotype; this gene masks the expression of alleles at the ABO locus. As mentioned earlier in the chapter, the alleles at the ABO locus encode antigens on the red blood cells; the antigens consist of short chains of carbohydrates embedded in the membranes of red blood cells. The difference between the A and the B antigens is a function of chemical differences in the terminal sugar of the chain. The IA and IB alleles actually encode different enzymes, which add sugars designated A or B to the ends of the carbohydrate chains (Figure 5.8). The common substrate on which these enzymes act is a molecule called H. The enzyme encoded by the i allele apparently either adds no sugar to H or no functional enzyme is specified.
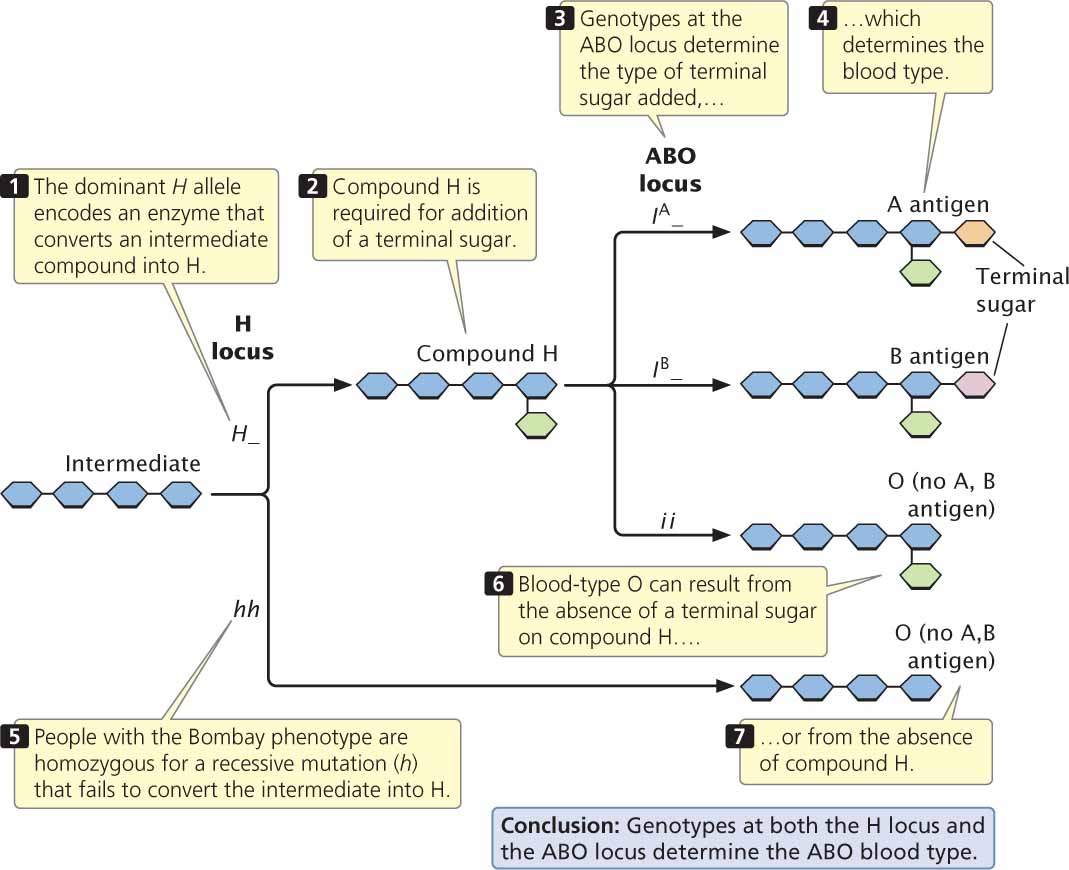
In most people, a dominant allele (H) at the H locus encodes an enzyme that makes H, but people with the Bombay phenotype are homozygous for a recessive mutation (h) that encodes a defective enzyme. The defective enzyme is incapable of making H and, because H is not produced, no ABO antigens are synthesized. Thus, the expression of the alleles at the ABO locus depends on the genotype at the H locus.
| Genotype | H present | ABO phenotype |
|---|---|---|
| H_ IAIA, H_ IAi | Yes | A |
| H_ IBIB, H_ IBi | Yes | B |
| H_ IAIB | Yes | AB |
| H_ ii | Yes | O |
| hh IAIA, hh IAi, hh IBIB, hh IBi,hh IAIB, and hh ii | No | O |
In this example, the alleles at the ABO locus are hypostatic to the recessive h allele.
The Bombay phenotype provides us with a good opportunity for considering how epistasis often arises when genes affect a series of steps in a biochemical pathway. The ABO antigens are produced in a multistep biochemical pathway (see Figure 5.8), which depends on enzymes that make H and on other enzymes that convert H into the A or B antigen. Note that blood-type O may arise in one of two ways: (1) from failure to add a terminal sugar to compound H (genotype H_ ii) or (2) from failure to produce compound H (genotype hh__). Many cases of epistasis arise in this way. A gene (such as h) that has an effect on an early step in a biochemical pathway will be epistatic to genes (such as IA and IB) that affect subsequent steps, because the effects of the genes in a later step depend on the product of the earlier reaction.
Dominant EpistasisIn recessive epistasis, the presence of two recessive alleles (the homozygous genotype) inhibits the expression of an allele at a different locus. However, in dominant epistasis, only a single copy of an allele is required to inhibit the expression of the allele at a different locus.
Dominant epistasis is seen in the interaction of two loci that determine fruit color in summer squash, which is commonly found in one of three colors: yellow, white, or green. When a homozygous plant that produces white squash is crossed with a homozygous plant that produces green squash and the F1 plants are crossed with each other, the following results are obtained:
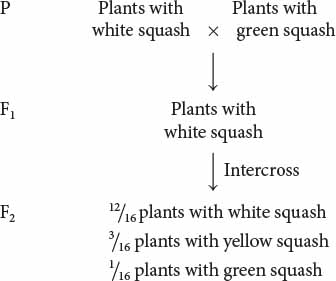
How can gene interaction explain these results?
In the F2, 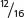 , or
, or 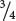 , of the plants produce white squash and
, of the plants produce white squash and 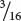 +
+ 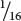 =
= 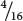 =
= 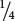 of the plants produce squash having color. This outcome is the familiar 3 : 1 ratio produced by a cross between two heterozygotes, which suggests that a dominant allele at one locus inhibits the production of pigment, resulting in white progeny. If we use the symbol W to represent the dominant allele that inhibits pigment production, then genotype W_ inhibits pigment production and produces white squash, whereas ww allows pigment and results in colored squash.
of the plants produce squash having color. This outcome is the familiar 3 : 1 ratio produced by a cross between two heterozygotes, which suggests that a dominant allele at one locus inhibits the production of pigment, resulting in white progeny. If we use the symbol W to represent the dominant allele that inhibits pigment production, then genotype W_ inhibits pigment production and produces white squash, whereas ww allows pigment and results in colored squash.
Among those ww F2 plants with pigmented fruit, we observe 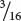 yellow and
yellow and 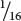 green (a 3 : 1 ratio). In this outcome, a second locus determines the type of pigment produced in the squash, with yellow (Y_) dominant over green (yy). This locus is expressed only in ww plants, which lack the dominant inhibitory allele W. We can assign the genotype ww Y_ to plants that produce yellow squash and the genotype ww yy to plants that produce green squash. The genotypes and their associated phenotypes are:
green (a 3 : 1 ratio). In this outcome, a second locus determines the type of pigment produced in the squash, with yellow (Y_) dominant over green (yy). This locus is expressed only in ww plants, which lack the dominant inhibitory allele W. We can assign the genotype ww Y_ to plants that produce yellow squash and the genotype ww yy to plants that produce green squash. The genotypes and their associated phenotypes are:
| W_ Y_ | white squash |
| W_ yy | white squash |
| ww Y_ | yellow squash |
| ww yy | green squash |
Allele W is epistatic to Y and y: it masks the expression of these pigment-producing genes. Allele W is a dominant epistatic allele because, in contrast with e in Labrador retriever coat color and with h in the Bombay phenotype, a single copy of the allele is sufficient to inhibit pigment production.
Yellow pigment in the squash is most likely produced in a two-step biochemical pathway (Figure 5.9). A colorless (white) compound (designated A in Figure 5.9) is converted by enzyme I into green compound B, which is then converted into compound C by enzyme II. Compound C is the yellow pigment in the fruit. Plants with the genotype ww produce enzyme I and may be green or yellow, depending on whether enzyme II is present. When allele Y is present at a second locus, enzyme II is produced and compound B is converted into compound C, producing a yellow fruit. When two copies of allele y, which does not encode a functional form of enzyme II, are present, squash remain green. The presence of W at the first locus inhibits the conversion of compound A into compound B; plants with genotype W_ do not make compound B and their fruit remains white, regardless of which alleles are present at the second locus.
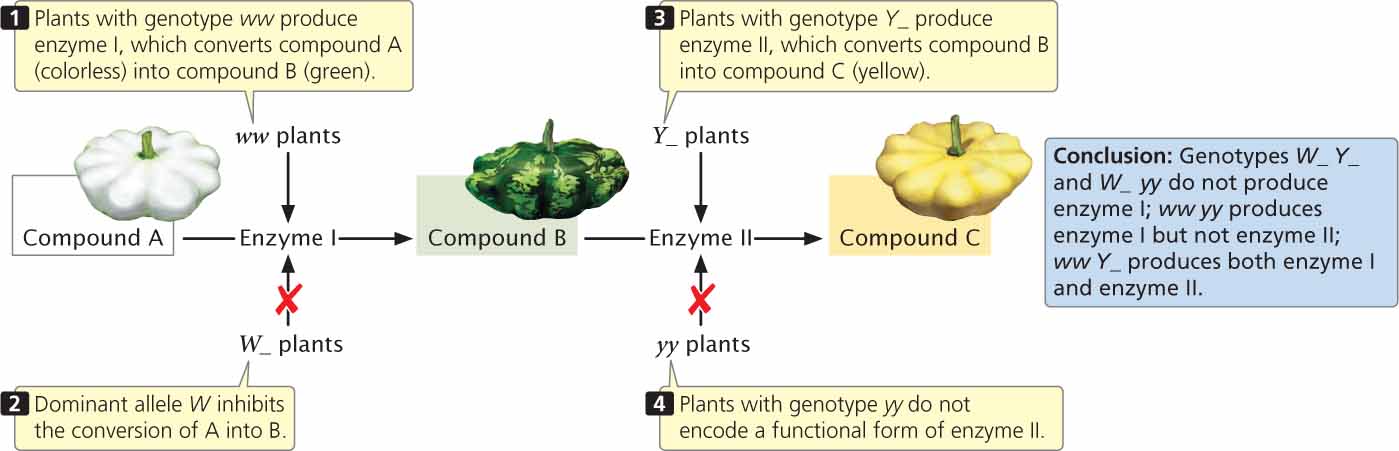
Duplicate Recessive EpistasisFinally, let’s consider duplicate recessive epistasis, in which two recessive alleles at either of two loci are capable of suppressing a phenotype. This type of epistasis is illustrated by albinism in snails.
Albinism is the absence of pigment and is a common genetic trait in many plants and animals. Pigment is almost always produced through a multistep biochemical pathway; thus, albinism may entail gene interaction. Robert T. Dillon and Amy R. Wethington found that albinism in the common freshwater snail Physa heterostropha can result from the presence of two recessive alleles at either of two different loci. Inseminated snails were collected from a natural population and placed in cups of water, where they laid eggs. Some of the eggs hatched into albino snails. When two albino snails were crossed, all of the F1 were pigmented. When the F1 were intercrossed, the F2 consisted of 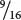 pigmented snails and
pigmented snails and 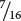 albino snails. How did this 9 : 7 ratio arise?
albino snails. How did this 9 : 7 ratio arise?
The 9 : 7 ratio seen in the F2 snails can be understood as a modification of the 9 : 3 : 3 : 1 ratio obtained when two individuals heterozygous for two loci are crossed. The 9 : 7 ratio arises when dominant alleles at both loci (A_ B_) produce pigmented snails; any other genotype produces albino snails:
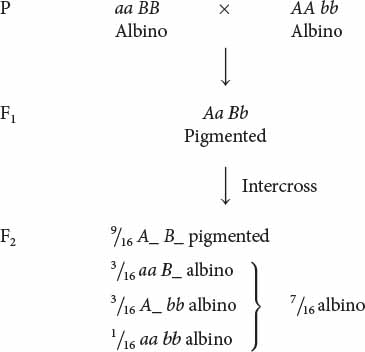
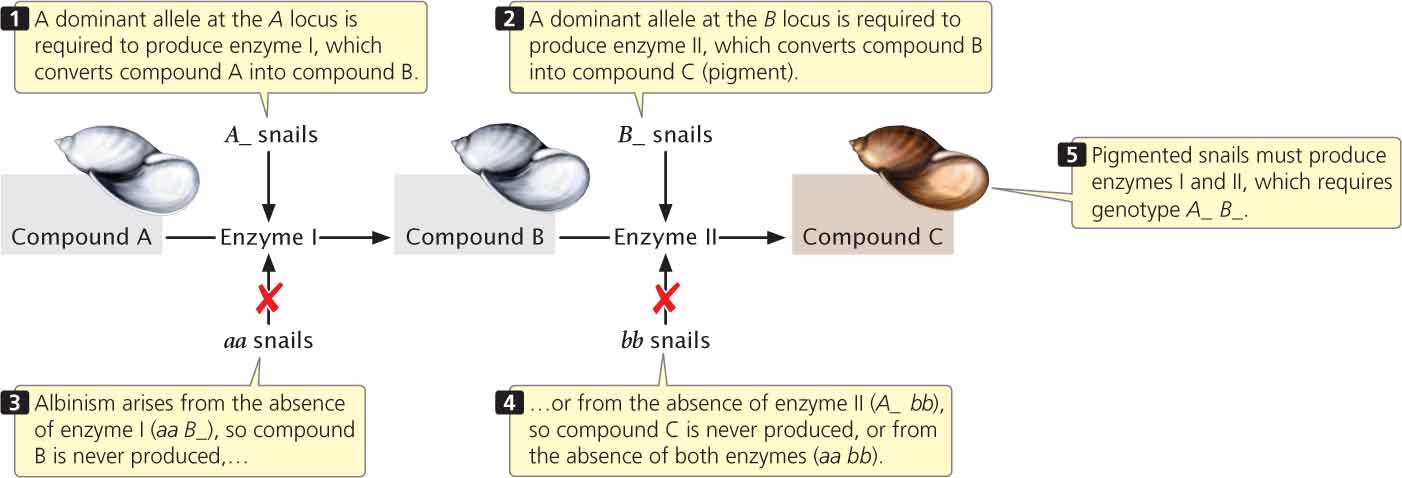
The 9 : 7 ratio in these snails is probably produced by a two-step pathway of pigment production (Figure 5.10). Pigment (compound C) is produced only after compound A has been converted into compound B by enzyme I and after compound B has been converted into compound C by enzyme II. At least one dominant allele A at the first locus is required to produce enzyme I; similarly, at least one dominant allele B at the second locus is required to produce enzyme II. Albinism arises from the absence of compound C, which may happen in one of three ways. First, two recessive alleles at the first locus (genotype aa B_) may prevent the production of enzyme I, and so compound B is never produced. Second, two recessive alleles at the second locus (genotype A_ bb) may prevent the production of enzyme II; in this case, compound B is never converted into compound C. Third, two recessive alleles may be present at both loci (aa bb), causing the absence of both enzyme I and enzyme II. In this example of gene interaction, a is epistatic to B, and b is epistatic to A; both are recessive epistatic alleles because the presence of two copies of either allele a or allele b is necessary to suppress pigment production. This example differs from the suppression of coat color in Labrador retrievers in that recessive alleles at either of two loci are capable of suppressing pigment production in the snails, whereas recessive alleles at a single locus suppress pigment expression in Labs.
CONCEPTS
Epistasis is the masking of the expression of one gene by another gene at a different locus. The epistatic gene does the masking; the hypostatic gene is masked. Epistatic alleles can be dominant or recessive.
 CONCEPT CHECK 7
CONCEPT CHECK 7A number of all-white cats are crossed and they produce the following types of progeny:  all-white,
all-white,  black, and
black, and  gray. What is the genotype of the black progeny?
gray. What is the genotype of the black progeny?
- Aa
- Aa Bb
- A_ B_
- A_ b
CONNECTING CONCEPTS
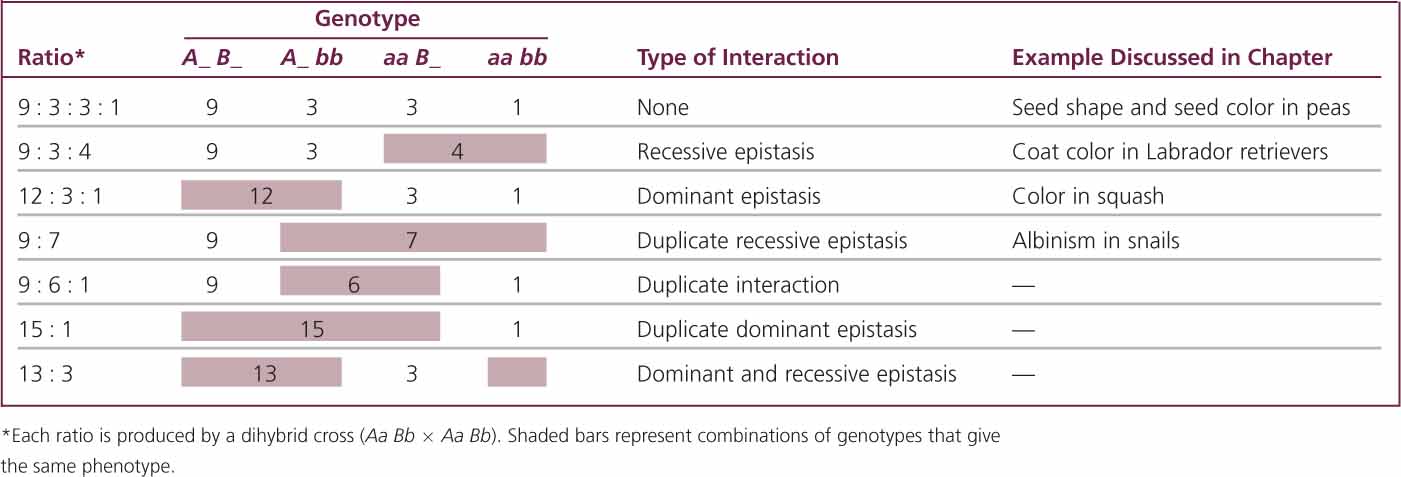
A number of modified ratios that result from gene interaction are shown in Table 5.2. Each of these examples represents a modification of the basic 9 : 3 : 3 : 1 dihybrid ratio. In interpreting the genetic basis of modified ratios, we should keep several points in mind. First, the inheritance of the genes producing these characteristics is no different from the inheritance of genes encoding simple genetic characters. Mendel’s principles of segregation and independent assortment still apply; each individual organism possesses two alleles at each locus, which separate in meiosis, and genes at the different loci assort independently. The only difference is in how the products of the genotypes interact to produce the phenotype. Thus, we cannot consider the expression of genes at each locus separately; instead, we must take into consideration how the genes at different loci interact.

A second point is that, in the examples that we have considered, the phenotypic proportions were always in sixteenths because, in all the crosses, pairs of alleles segregated at two independently assorting loci. The probability of inheriting one of the two alleles at a locus is 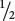 . Because there are two loci, each with two alleles, the probability of inheriting any particular combination of genes is (
. Because there are two loci, each with two alleles, the probability of inheriting any particular combination of genes is (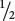 )4 =
)4 = 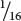 . For a trihybrid cross, the progeny proportions should be in sixty-fourths, because (
. For a trihybrid cross, the progeny proportions should be in sixty-fourths, because (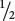 )6 =
)6 = 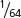 . In general, the progeny proportions should be in fractions of (
. In general, the progeny proportions should be in fractions of (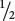 )2n, where n equals the number of loci with two alleles segregating in the cross.
)2n, where n equals the number of loci with two alleles segregating in the cross.
Crosses rarely produce exactly 16 progeny; therefore, modifications of a dihybrid ratio are not always obvious. Modified dihybrid ratios are more easily seen if the number of individuals of each phenotype is expressed in sixteenths:

where x/16 equals the proportion of progeny with a particular phenotype. If we solve for x (the proportion of the particular phenotype in sixteenths), we have:
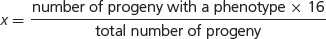
For example, suppose that we cross two homozygotes, interbreed the F1, and obtain 63 red, 21 brown, and 28 white F2 individuals. Using the preceding formula, we find the phenotypic ratio in the F2 to be: red = (63 × 16)/112 = 9; brown = (21 × 16)/112 = 3; and white = (28 × 16)/112 = 4. The phenotypic ratio is 9 : 3 : 4.
A final point to consider is how to assign genotypes to the phenotypes in modified ratios that result from gene interaction. Don’t try to memorize the genotypes associated with all the modified ratios in Table 5.2. Instead, practice relating modified ratios to known ratios, such as the 9 : 3 : 3 : 1 dihybrid ratio. Suppose that we obtain 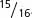 green progeny and
green progeny and 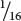 white progeny in a cross between two plants. If we compare this 15 : 1 ratio with the standard 9 : 3 : 3 : 1 dihybrid ratio, we see that
white progeny in a cross between two plants. If we compare this 15 : 1 ratio with the standard 9 : 3 : 3 : 1 dihybrid ratio, we see that 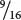 +
+ 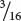 +
+ 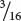 equals
equals 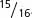 . All the genotypes associated with these proportions in the dihybrid cross (A_ B_, A_ bb, and aa B_) must give the same phenotype, the green progeny. Genotype aa bb makes up
. All the genotypes associated with these proportions in the dihybrid cross (A_ B_, A_ bb, and aa B_) must give the same phenotype, the green progeny. Genotype aa bb makes up 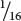 of the progeny in a dihybrid cross, the white progeny in this cross.
of the progeny in a dihybrid cross, the white progeny in this cross.
In assigning genotypes to phenotypes in modified ratios, students sometimes become confused about which letters to assign to which phenotype. Suppose that we obtain the following phenotypic ratio: 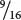 black :
black : 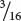 brown :
brown : 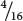 white. Which genotype do we assign to the brown progeny, A_ bb or aa B_? Either answer is correct because the letters are just arbitrary symbols for the genetic information. The important thing to realize about this ratio is that the brown phenotype arises when two recessive alleles are present at one locus.
white. Which genotype do we assign to the brown progeny, A_ bb or aa B_? Either answer is correct because the letters are just arbitrary symbols for the genetic information. The important thing to realize about this ratio is that the brown phenotype arises when two recessive alleles are present at one locus.
WORKED PROBLEM
A homozygous strain of yellow corn is crossed with a homozygous strain of purple corn. The F1 are intercrossed, producing an ear of corn with 119 purple kernels and 89 yellow kernels (the progeny). What is the genotype of the yellow kernels?
What information is required in your answer to the problem?
The genotype of the yellow kernels.
What information is provided to solve the problem?
 A homozygous yellow corn plant is crossed with a homozygous purple corn plant.
A homozygous yellow corn plant is crossed with a homozygous purple corn plant. The numbers of purple and yellow progeny produced by the cross.
The numbers of purple and yellow progeny produced by the cross.
We should first consider whether the cross between yellow and purple strains might be a monohybrid cross for a simple dominant trait, which would produce a 3 : 1 ratio in the F2 (Aa × Aa → 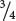 A_ and
A_ and 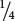 aa). Under this hypothesis, we would expect 156 purple progeny and 52 yellow progeny:
aa). Under this hypothesis, we would expect 156 purple progeny and 52 yellow progeny:
| Phenotype | Genotype | Observed number | Expected number |
|---|---|---|---|
| purple | A_ | 119 |
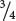 × 208 = 156
× 208 = 156 |
| yellow | aa | 89 |
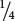 × 208 = 52
× 208 = 52 |
| Total | 208 |
We see that the expected numbers do not closely fit the observed numbers. If we performed a chi-square test (see Chapter 3), we would obtain a calculated chi-square value of 35.08, which has a probability much less than 0.05, indicating that it is extremely unlikely that, when we expect a 3 : 1 ratio, we would obtain 119 purple progeny and 89 yellow progeny. Therefore, we can reject the hypothesis that these results were produced by a monohybrid cross.
Another possible hypothesis is that the observed F2 progeny are in a 1 : 1 ratio. However, we learned in Chapter 3 that a 1 : 1 ratio is produced by a cross between a heterozygote and a homozygote (Aa × aa) and, from the information given, the cross was not between a heterozygote and a homozygote, because both original parental strains were homozygous. Furthermore, a chi-square test comparing the observed numbers with an expected 1 : 1 ratio yields a calculated chi-square value of 4.32, which has a probability of less than 0.05.
Next, we should look to see if the results can be explained by a dihybrid cross (Aa Bb × Aa Bb). A dihybrid cross results in phenotypic proportions that are in sixteenths. We can apply the formula given earlier in the chapter to determine the number of sixteenths for each phenotype:

Thus, purple and yellow appear in an approximate ratio of 9 : 7
We can test this hypothesis with a chi-square test:
| Phenotype | Genotype | Observed number | Expected number |
|---|---|---|---|
| purple | ? | 119 |
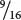 × 208 = 117
× 208 = 117 |
| yellow | ? | 89 |
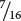 × 208 = 91
× 208 = 91 |
| Total | 208 |

Degree of freedom = n − 1 = 2 − 1 = 1
P > 0.05
The probability associated with the chi-square value is greater than 0.05, indicating that there is a good fit between the observed results and a 9 : 7 ratio.
We now need to determine how a dihybrid cross can produce a 9 : 7 ratio and what genotypes correspond to the two phenotypes. A dihybrid cross without epistasis produces a 9 : 3 : 3 : 1 ratio:
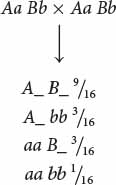
Because 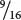 of the progeny from the corn cross are purple, purple must be produced by genotypes A_ B_; in other words, individual kernels that have at least one dominant allele at the first locus and at least one dominant allele at the second locus are purple. The proportions of all the other genotypes (A_ bb, aa B_, and aa bb) sum to
of the progeny from the corn cross are purple, purple must be produced by genotypes A_ B_; in other words, individual kernels that have at least one dominant allele at the first locus and at least one dominant allele at the second locus are purple. The proportions of all the other genotypes (A_ bb, aa B_, and aa bb) sum to 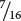 , which is the proportion of the progeny in the corn cross that are yellow, and so any individual kernel that does not have a dominant allele at both the first and the second locus is yellow.
, which is the proportion of the progeny in the corn cross that are yellow, and so any individual kernel that does not have a dominant allele at both the first and the second locus is yellow.
Now test your understanding of epistasis by working Problem 26 at the end of the chapter.
Complementation: Determining Whether Mutations Are at the Same Locus or at Different Loci
How do we know whether different mutations that affect a characteristic occur at the same locus (are allelic) or at different loci? In fruit flies, for example, white is an X-linked recessive mutation that produces white eyes instead of the red eyes found in wild-type flies; apricot is an X-linked recessive mutation that produces light-orange-colored eyes. Do the white and apricot mutations occur at the same locus or at different loci? We can use the complementation test to answer this question.
To carry out a complementation test on recessive mutations, parents that are homozygous for different mutations are crossed, producing offspring that are heterozygous. If the mutations are allelic (occur at the same locus), then the heterozygous offspring have only mutant alleles (a b) and exhibit a mutant phenotype:
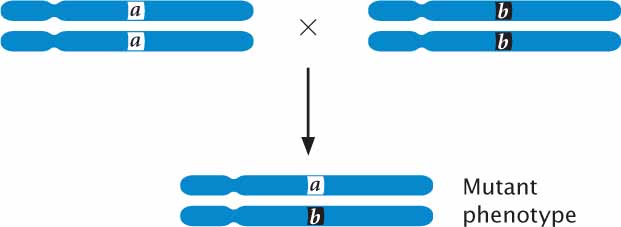
If, on the other hand, the mutations occur at different loci, each of the homozygous parents possesses wild-type genes at the other locus (aa b+b+ and a+a+ bb); so the heterozygous offspring inherit a mutant allele and a wild-type allele at each locus. In this case, the presence of a wild type allele complements the mutation at each locus and the heterozygous offspring have the wild-type phenotype:
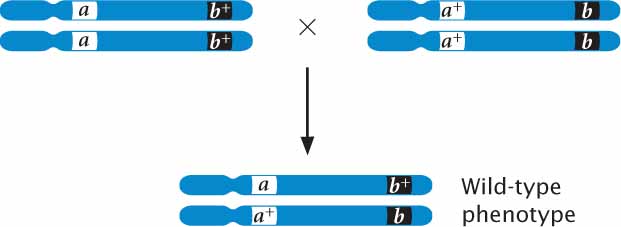
Complementation has taken place if an individual organism possessing two recessive mutations has a wild-type phenotype, indicating that the mutations are nonallelic genes. There is a lack of complementation when two recessive mutations occur at the same locus, producing a mutant phenotype.
When the complementation test is applied to white and apricot mutations, all of the heterozygous offspring have light-colored eyes, demonstrating that white eyes and apricot eyes are produced by mutations that occur at the same locus and are allelic.
CONCEPTS
A complementation test is used to determine whether two mutations occur at the same locus (are allelic) or at different loci.
 CONCEPT CHECK 8
CONCEPT CHECK 8Brindle (tiger-striped appearance) is a recessive trait in bulldogs and in Chihuahuas. What types of crosses would you carry out to determine whether the brindle genes in bulldogs and in Chihuahuas are at the same locus?
The Complex Genetics of Coat Color in Dogs
The genetics of coat color in dogs is an excellent example of how complex interactions between genes may take part in the determination of a phenotype. Domestic dogs come in an amazing variety of shapes, sizes, and colors. For thousands of years, people have been breeding dogs for particular traits, producing the large number of types that we see today. Each breed of dog carries a selection of alleles from the ancestral dog gene pool; these alleles define the features of a particular breed. The genome of the domestic dog was completely sequenced in 2004, greatly facilitating the study of canine genetics.
We will consider four loci (in the list that follows) that are important in producing many of the noticeable differences in color and pattern among breeds of dogs. In interpreting the genetic basis of differences in the coat color of dogs, consider how the expression of a particular gene is modified by the effects of other genes. Keep in mind that additional loci not listed here can modify the colors produced by these four loci and that not all geneticists agree on the genetics of color variation in some breeds.
- 1. Agouti (A) locus. This locus has five common alleles that determine the depth and distribution of color in a dog’s coat:
As Solid black pigment. aw Agouti, or wolflike gray. Hairs encoded by this allele have a “salt and pepper” appearance, produced by a band of yellow pigment on a black hair. ay Yellow. The black pigment is markedly reduced; so the entire hair is yellow. as Saddle markings (dark color on the back, with extensive tan markings on the head and legs). at Bicolor (dark color over most of the body, with tan markings on the feet and eyebrows). Alleles As and ay are generally dominant over the other alleles, but the dominance relations are complex and not yet completely understood.
- 2. Black (B) locus. This locus determines whether black pigment can be formed. The actual color of a dog’s coat depends on the effects of genes at other loci (such as the A and E loci). Two alleles are common:
B Allows black pigment to be produced. b Black pigment cannot be produced; pigmented dogs can be chocolate, liver, tan, or red. Allele B is dominant over allele b.
- 3. Extension (E) locus. Four alleles at this locus determine where the genotype at the A locus is expressed. For example, if a dog has the As allele (solid black) at the A locus, then black pigment will either be extended throughout the coat or be restricted to some areas, depending on the alleles present at the E locus. Areas where the A locus is not expressed may appear as yellow, red, or tan, depending on the presence of particular genes at other loci. When As is present at the A locus, the four alleles at the E locus have the following effects:
Em Black mask with a tan coat. E The A locus expressed throughout (solid black). ebr Brindle, in which black and yellow are in layers to give a tiger-striped appearance. e No black in the coat, but the nose and eyes may be black. The dominance relations among these alleles are poorly known.
- 4. Spotting (S) locus. Alleles at this locus determine whether white spots will be present. There are four common alleles:
S No spots. si Irish spotting; numerous white spots. sp Piebald spotting; various amounts of white. sw Extreme white piebald; almost all white. Allele S is completely dominant over alleles si, sp, and sw; alleles si and sp are dominant over allele sw (S > si, sp > sw). The relation between si and sp is poorly defined; indeed, they may not be separate alleles. Genes at other poorly known loci also modify spotting patterns.
To illustrate how genes at these loci interact in determining a dog’s coat color, let’s consider a few examples.
Labrador RetrieverLabrador retrievers (Figure 5.11a) may be black, brown, or yellow. Most are homozygous ASAS SS; thus, they vary only at the B and E loci. The As allele allows dark pigment to be expressed; whether a dog is black depends on which genes are present at the B and E loci. As discussed earlier in the chapter, all black Labradors must carry at least one B allele and one E allele (B_ E_). Brown dogs are homozygous bb and have at least one E allele (bb E_). Yellow dogs are a result of the presence of ee (B_ ee or bb ee). Labrador retrievers are homozygous for the S allele, which produces a solid color; the few white spots that appear in some dogs of this breed are due to other modifying genes.

BeagleMost beagles (Figure 5.11b) are homozygous asas BB spsp, although other alleles at these loci are occasionally present. The as allele produces the saddle markings—dark back and sides, with tan head and legs—that are characteristic of the breed. Allele B allows black to be produced, but its distribution is limited by the as allele. Most beagles are E_, but the genotype ee does occasionally arise, leading to a few all-tan beagles. White spotting in beagles is due to the sp allele.
DalmatianDalmatians (Figure 5.11c) have an interesting genetic makeup. Most are homozygous AsAs EE swsw; so they vary only at the B locus. Notice that these dogs possess genotype AsAs EE, which allows for a solid coat that would be black, if genotype B_ were present, or brown (called liver), if genotype bb were present. However, the presence of the sw allele produces a white coat, masking the expression of the solid color. The dog’s color appears only in the pigmented spots, which are due to the presence of an allele at yet another locus that allows the color to penetrate in a limited number of spots.
Table 5.3 gives the common genotypes of other breeds of dogs.  TRY PROBLEM 33
TRY PROBLEM 33
| Breed | Usual Homozygous Genotypes* | Other Alleles Present Within the Breed |
|---|---|---|
| Basset hound | BB EE | ay, at S, sP, si |
| Beagle | asas BB sPsP | E, e |
| English bulldog | BB | As, ay, at Em, E, ebr S, si, sP, sw |
| Chihuahua | As, ay, as, at B, b Em, E, ebr, e S, si, sP, sw | |
| Collie | BB EE | ay, at si, sw |
| Dalmatian | ASAS EE swsw | B, b |
| Doberman | atat EE SS | B, b |
| German shepherd | BB SS | ay, a, as, at Em, E, e |
| Golden retriever | ASAS BB SS | E, e |
| Greyhound | BB | As, ay E, ebr, e S, sP, sw, si |
| Irish setter | BB ee SS | A, at |
| Labrador retriever | ASAS SS | B, b E, e |
| Poodle | SS | As, at B, b E, e |
| Rottweiler | atat BB EE SS | |
| St. Bernard | ayay BB | Em, E si, sp, sw |
| *Most dogs in the breed are homozygous for these genes; a few individual dogs may possess other alleles at these loci. | ||
| Source: Data from M. B. Willis, Genetics of the Dog (London: Witherby, 1989). | ||