Applying Probability and the Branch Diagram to Dihybrid Crosses
When the genes at two loci separate independently, a dihybrid cross can be understood as two monohybrid crosses. Let’s examine Mendel’s dihybrid cross (Rr Yy × Rr Yy) by considering each characteristic separately (Figure 3.10a). If we consider only the shape of the seeds, the cross was Rr × Rr, which yields a 3:1 phenotypic ratio (¾ round and ¼ wrinkled progeny; see Table 3.2). Next consider the other characteristic, the color of the seed. The cross was Yy × Yy, which produces a 3:1 phenotypic ratio (¾ yellow and ¼ green progeny).
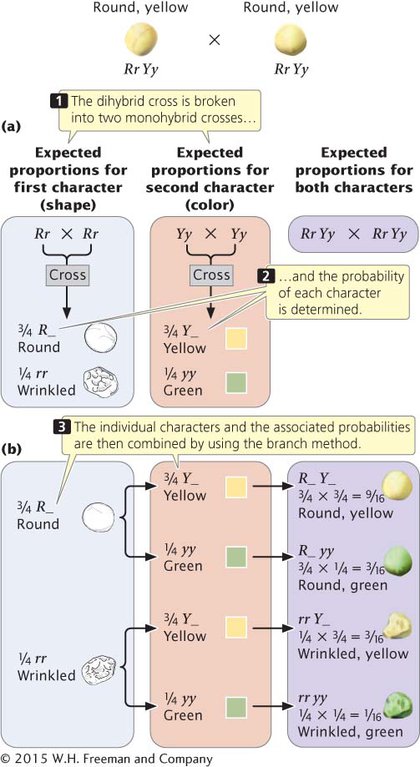
We can now combine these monohybrid ratios by using the multiplication rule to obtain the proportion of progeny with different combinations of seed shape and color. The proportion of progeny with round and yellow seeds is ¾ (the probability of round) × ¾ (the probability of yellow) = 9/16. The proportion of progeny with round and green seeds is ¾ × ¼ = 3/16; the proportion of progeny with wrinkled and yellow seeds is ¼ × ¾ = 3/16; and the proportion of progeny with wrinkled and green seeds is ¼ × ¼ = 1/16.
Branch diagrams are a convenient way of organizing all the combinations of characteristics (Figure 3.10b). In the first column, list the proportions of the phenotypes for one characteristic (here, ¾ round and ¼ wrinkled). In the second column, list the proportions of the phenotypes for the second characteristic (¾ yellow and ¼ green) twice, next to each of the phenotypes in the first column: list ¾ yellow and ¼ green next to the round phenotype and again next to the wrinkled phenotype. Draw lines between the phenotypes in the first column and each of the phenotypes in the second column. Now follow each branch of the diagram, multiplying the probabilities for each trait along that branch. One branch leads from round to yellow, yielding round and yellow progeny. Another branch leads from round to green, yielding round and green progeny, and so forth. We can then calculate the probability of progeny with a particular combination of traits by using the multiplication rule, as shown above: the probability of round (¾) and yellow (¾) seeds, for example, is ¾ × ¾ = 9/16. The advantage of the branch diagram is that it helps us keep track of all the potential combinations of traits that may appear in the progeny. It can be used to determine phenotypic or genotypic ratios for any number of characteristics.
Using probability is much faster than using the Punnett square for crosses that include multiple loci. Genotypic and phenotypic ratios can be quickly worked out by combining, with the multiplication rule, the simple ratios in Tables 3.2 and 3.3. The probability method is particularly efficient if we need the probability of only a particular phenotype or genotype among the progeny of a cross. Suppose that we need to know the probability of obtaining the genotype Rr yy in the F2 of the dihybrid cross in Figure 3.8. The probability of obtaining the Rr genotype in a cross of Rr × Rr is ½, and that of obtaining the yy genotype in a cross of Yy × Yy is ¼ (see Table 3.3). Using the multiplication rule, we find the probability of Rr yy to be ½ × ¼ = ⅛.
To illustrate the advantage of the probability method, consider the cross Aa Bb cc Dd Ee × Aa Bb Cc dd Ee. Suppose that we want to know the probability of obtaining offspring with the genotype aa bb cc dd ee. If we use a Punnett square to determine this probability, we might be working on the solution for months. However, we can quickly figure the probability of obtaining this one genotype by breaking this cross into a series of single-
| Progeny cross | Genotype | Probability |
|---|---|---|
| Aa × Aa | aa | ¼ |
| Bb × Bb | bb | ¼ |
| Cc × Cc | cc | ½ |
| Dd × dd | dd | ½ |
| Ee × Ee | ee | ¼ |
The probability of an offspring from this cross having genotype aa bb cc dd ee is now easily obtained by using the multiplication rule: ¼ × ¼ × ½ × ½ × ¼ = 1/256. This calculation assumes that the genes at these five loci all assort independently.
CONCEPTS
A cross including several characteristics can be worked by breaking it down into single-
Now that you’ve had some experience working genetic crosses, explore Mendel’s principles of heredity by setting up some of your own crosses in Animation 3.1.