Problem 1

A series of two-point crosses were carried out among seven loci (a, b, c, d, e, f, and g), producing the following recombination frequencies. Using these recombination frequencies, map the seven loci, showing their linkage groups, the order of the loci in each linkage group, and the distances between the loci of each group.

Solution Strategy

What information is required in your answer to the problem?

The linkage groups for the seven loci, the order of the loci within each linkage group, and the map distances between the loci.

What information is provided to solve the problem?

For help with this problem, review:

Constructing a Genetic Map with Two-Point Testcrosses in Section 5.2.

Solution Steps

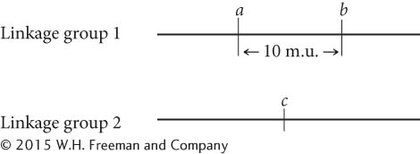
To work this problem, remember that 1% recombination equals 1 map unit. The recombination frequency between a and b is 10%; so these two loci are in the same linkage group, approximately 10 m.u. apart.

The recombination frequency between a and c is 50%; so c must lie in a second linkage group.

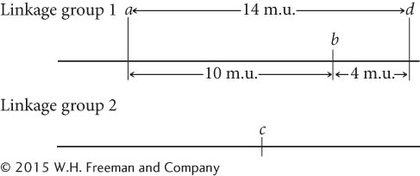
The recombination frequency between a and d is 14%; so d is located in linkage group 1. Is locus d 14 m.u. to the right or to the left of gene a? If d is 14 m.u. to the left of a, then the b-to-d distance should be 10 m.u. + 14 m.u. = 24 m.u. On the other hand, if d is to the right of a, then the distance between b and d should be 14 m.u. −10 m.u. = 4 m.u. The b–d recombination frequency is 4%; so d is 14 m.u. to the right of a. The updated map is

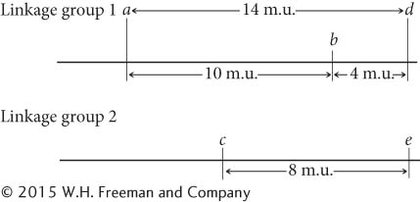
The recombination frequencies between each of loci a, b, and d and locus e are all 50%; so e is not in linkage group 1 with a, b, and d. The recombination frequency between e and c is 8%; so e is in linkage group 2:

142

There is 50% recombination between f and all the other genes; so f must belong to a third linkage group:

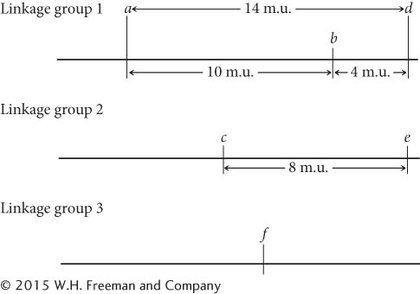
Finally, position locus g with respect to the other genes. The recombination frequencies between g and loci a, b, and d are all 50%; so g is not in linkage group 1. The recombination frequency between g and c is 12%; so g is a part of linkage group 2. To determine whether g is 12 m.u. to the right or left of c, consult the g–e recombination frequency. Because this recombination frequency is 18%, g must lie to the left of c:

Note that the g-to-e distance (18 m.u.) is shorter than the sum of the g-to-c (12 m.u.) and c-to-e distances (8 m.u.) because of undetectable double crossovers between g and e.

Problem 2

Ebony body color (e), rough eyes (ro), and brevis bristles (bv) are three recessive mutations that occur in fruit flies. The loci for these mutations have been mapped and are separated by the following map distances:

The interference between these genes is 0.4.

A fly with ebony body, rough eyes, and brevis bristles is crossed with a fly that is homozygous for the wild-type traits. The resulting F₁ females are test-crossed with males that have ebony body, rough eyes, and brevis bristles; 1800 progeny are produced. Give the expected numbers of phenotypes in the progeny of the testcross.

Solution Strategy

What information is required in your answer to the problem?

The expected numbers of different phenotypes produced by the testcross.

What information is provided to solve the problem?

For help with this problem, review:

Constructing a Genetic Map with a Three-Point Testcross and the Worked Problem in Section 5.3.

143

Solution Steps

The crosses are

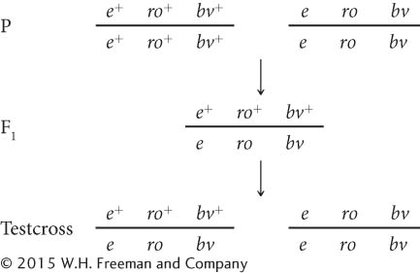
In this case, we know that ro is the middle locus because the genes have been mapped. Eight classes of progeny will be produced by this cross:

To determine the numbers of each type, use the map distances, starting with the double crossovers. The expected number of double crossovers is equal to the product of the single-crossover probabilities:

However, there is some interference; so the observed number of double crossovers will be less than the expected. The interference is 1 – coefficient of coincidence; so the coefficient of coincidence is

coefficient of coincidence = 1 – interference

The interference is given as 0.4; so the coefficient of coincidence equals 1 − 0.4 = 0.6. Recall that the coefficient of coincidence is

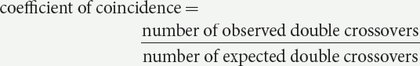
Rearranging this equation, we obtain:

number of observed double crossovers = coefficient of coincidence × number of expected double crossovers

number of observed double crossovers = 0.6 × 43.2 = 26

A total of 26 double crossovers should be observed. Because there are two classes of double crossovers (e⁺       ro       bv⁺ and e       ro⁺       bv), we expect to observe 13 of each class.

Next, we determine the number of single-crossover progeny. The genetic map indicates that the distance between e and ro is 20 m.u.; so 360 progeny (20% of 1800) are expected to have resulted from recombination between these two loci. Some of them will be single-crossover progeny and some will be double-crossover progeny. We have already determined that the number of double-crossover progeny is 26; so the number of progeny resulting from a single crossover between e and ro is 360 − 26 = 334, which will be divided equally between the two single-crossover phenotypes (e       ro⁺       bv⁺ and e⁺       ro       bv).

The distance between ro and bv is 12 m.u.; so the number of progeny resulting from recombination between these two genes is 0.12 × 1800 = 216. Again, some of these recombinants will be single-crossover progeny and some will be double-crossover progeny. To determine the number of progeny resulting from a single crossover, subtract the double crossovers: 216 – 26 = 190. These single-crossover progeny will be divided between the two single-crossover phenotypes (e⁺       ro⁺       bv and e       ro       bv⁺); so there will be ¹⁹⁰/₂ = 95 of each of these phenotypes. The remaining progeny will be nonrecombinants, and they can be obtained by subtraction: 1800 – 26 – 334 – 190 = 1250; there are two nonrecombinants (e⁺       ro⁺       bv⁺ and e       ro       bv); so there will be ¹²⁵⁰/₂ = 625 of each. The numbers of the various phenotypes are listed here: