Example 1.32

EXAMPLE 1.32 Using the 68-95-99.7 Rule

The distribution of weights of 9-ounce bags of a particular brand of potato chips is approximately Normal with mean ounce and standard deviation ounce. Figure 1.24 shows what the 68-95-99.7 rule says about this distribution.

Figure 1.26: FIGURE 1.24 The 68-95-99.7 rule applied to the distribution of weights of bags of potato chips, Example 1.32.

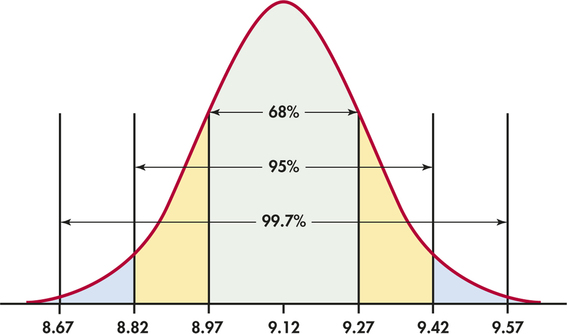
Two standard deviations is 0.3 ounce for this distribution. The 95 part of the 68-95-99.7 rule says that the middle 95% of 9-ounce bags weigh between and ounces, that is, between 8.82 ounces and 9.42 ounces. This fact is exactly true for an exactly Normal distribution. It is approximately true for the weights of 9-ounce bags of chips because the distribution of these weights is approximately Normal.

The other 5% of bags have weights outside the range from 8.82 to 9.42 ounces. Because the Normal distributions are symmetric, half of these bags are on the heavy side. So the heaviest 2.5% of 9-ounce bags are heavier than 9.42 ounces.

The 99.7 part of the 68-95-99.7 rule says that almost all bags (99.7% of them) have weights between and . This range of weights is 8.67 to 9.57 ounces.