EXAMPLE 11.23 An Alternative Bath Model

CASE 11.3 Starting again with one-bath homes as the base (all indicator variables 0), let B2 be an indicator variable for an extra full bath and let Bh be an indicator variable for an extra half bath. Thus, a home with two baths has $\text{Bh}=0$ and $\text{B}2=1$. A home with 2.5 baths has $\text{Bh}=1$ and $\text{B}2=1$. Regressing Price on Bh and B2 gives the output in Figure 11.20.

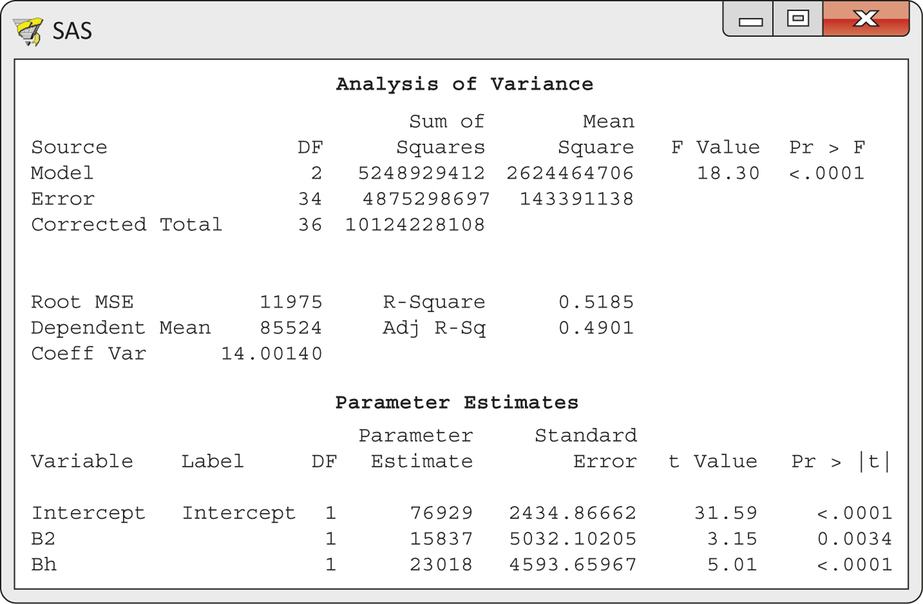
The overall model is statistically significant ($F=18.30$, $\text{df}=2\text{and}34$, $P<0.0001$), and it explains 51.9% of the variation in price. This compares favorably with the 53.3% explained by the model with three indicator variables for bathrooms. The fitted model is

That is, an extra full bath adds $15,837 to the mean price and an extra half bath adds $23,018. The $t$ statistics show that both regression coefficients are significantly different from zero ($t=3.15$, $\text{df}=34$, $P=0.0034$; and $t=5.01$, $\text{df}=34$, $P<0.0001$).