Example 12.2

EXAMPLE 12.2 Constructing $\bar{x}$ and $R$ Charts

lab

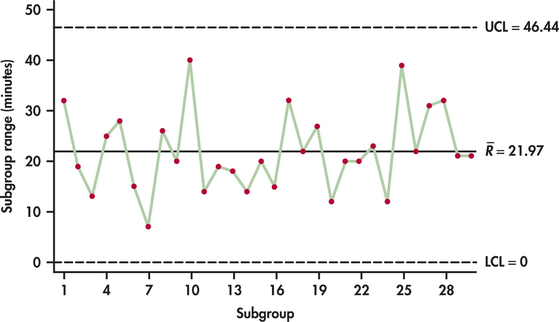
CASE 12.1 We begin the analysis of the turnaround times for the lab-testing process by focusing on the process variability. We use the 30 ranges shown in Table 12.2 to find the average range:

$\begin{array}{l} \bar{R} & = & \frac{1}{30} (32 + 19 + \dots + 21) \\ = & \frac{659}{30} = 21.967 \end{array}$

Page 606

From Table 12.1 (page 603), for subgroup size $n = 5$ , the values of $D_{3}$ and $D_{4}$ are 0 and 2.114, respectively. Accordingly, the center line and control limits for the $R$ chart are

$\begin{array}{l} UCL & = & D_{4} \bar{R} = 2.114 (21.967) = 46.438 \\ CL & = & \bar{R} = 21.967 \\ LCL & = & D_{3} \bar{R} = 0 (21.967) = 0 \end{array}$

Figure 12.3 shows the $R$ chart for the lab-testing process. The $R$ chart shows no points outside the upper control limit. Furthermore, the ranges plotted over time show no unusual pattern. We can say that from the perspective of process variation, the process is in control.

FIGURE 12.3

$R$ chart for the lab-testing data of Table 12.2.

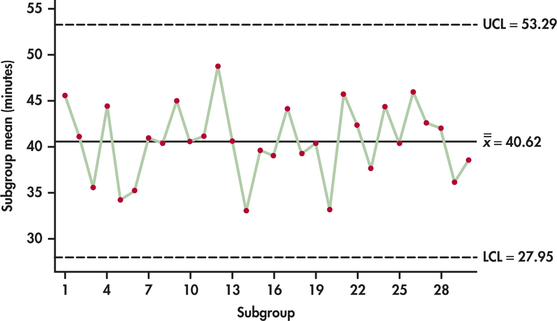
We now construct the $\bar{x}$ chart. Because the $R$ chart exhibited in-control behavior, we can safely use the value of 21.967 computed earlier for $\bar{R}$ in the computation of the $\bar{x}$ chart limits. Referring to Table 12.2, we can find the grand mean:

$\begin{array}{l} \bar{\bar{x}} & = & \frac{1}{30} (45.6 + 41.2 + \dots + 38.6) \\ = & \frac{1218.6}{30} = 40.62 \end{array}$

From Table 12.1 (page 603), we find $A_{2} = 0.577$ . The center line and control limits for the $\bar{x}$ chart are then as follows:

$\begin{array}{l} UCL & = & \bar{\bar{x}} + A_{2} \bar{R} = 40.62 + 0.577 (21.967) = 53.29 \\ CL & = & \bar{\bar{x}} = 40.62 \\ LCL & = & \bar{\bar{x}} - A_{2} \bar{R} = 40.62 - 0.577 (21.967) = 27.95 \end{array}$

Figure 12.4 shows the $\bar{x}$ chart. The subgroup means of the 30 samples do vary, but all lie within the range of variation marked out by the control limits. We are seeing the common cause variation of a stable process with no indications of special causes.

Page 607

FIGURE 12.4

$\bar{x}$ chart for the lab-testing data of Table 12.2.