Example 12.9

EXAMPLE 12.9 O-Ring Process Capability

oring

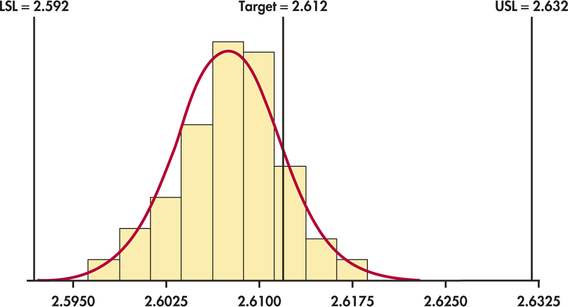
CASE 12.2 At the conclusion of the process study in Example 12.3 (pages 610–612), we found two special causes and eliminated from our data the subgroups on which those causes operated. From Figure 12.9 (page 612), after removal of the two subgroups, we find $\bar{\bar{x}} = 2.60756$ and $\bar{R} = 0.00899$ . As noted in Case 12.2 (page 609), specification limits for the inside diameter are set at $2.612 \pm 0.02$ inches, which implies $LSL = 2.592$ and $USL = 2.632$ . Figure 12.16 shows that the individual measurements are compatible with the Normal distribution.

Page 624

FIGURE 12.16 Comparing the distribution of O-ring measurements with lower and upper specification limits, Example 12.9.

From Table 12.1 (page 603), we find $d_{2} = 2.059$ for $n = 4$ , which gives the estimate for $σ$

$\hat{σ} = \frac{0.00899}{2.059} = 0.004366$

In addition, the mean estimate $\hat{μ}$ is simply the grand mean $\bar{\bar{x}}$ . These estimates may be quite accurate if we have data on many past samples.

Estimates based on only a few observations may, however, be inaccurate because statistics from small samples can have large sampling variability. This important point is often not appreciated when capability indices are used in practice. To emphasize that we can only estimate the indices, we write ${\hat{C}}_{p}$ and ${\hat{C}}_{p k}$ for values calculated from sample data. They are

$\begin{array}{l} {\hat{C}}_{p} & = & \frac{USL - LSL}{6 \hat{σ}} \\ = & \frac{2.632 - 2.592}{(6) (0.004366)} = 1.53 \\ {\hat{C}}_{p k} & = & \min (\frac{\hat{μ} - LSL}{3 \hat{σ}}, \frac{USL - \hat{μ}}{3 \hat{σ}}) \\ = & \min (\frac{2.60756 - 2.592}{(3) (0.004366)}, \frac{2.632 - 2.60756}{(3) (0.004366)}) \\ = & \min (1.19, 1.87) = 1.19 \end{array}$

Both indices are well above 1, which indicates that we have a highly capable process. However, the fact that ${\hat{C}}_{p k}$ is markedly smaller than ${\hat{C}}_{p}$ indicates that the process is off target. Indeed, a close look at Figure 12.16 shows that the center of the distribution is to the left of the center of the specs. If we can adjust the center of the process distribution to the target of 2.612, then ${\hat{C}}_{p k}$ will increase and will equal ${\hat{C}}_{p}$ .