Example 16.7

EXAMPLE 16.7 Loss of Product Value: Rank Test

vitc

In the vitamin loss study of Example 16.6, $n = 9$ . If the null hypothesis (no systematic loss of vitamin C) is true, the mean of the signed rank statistic is

$μ_{W^{+}} = \frac{n (n + 1)}{4} = \frac{(9) (10)}{4} = 22.5$

Our observed value $W^{+} = 34$ is somewhat larger than this mean. The one-sided $P$ -value is $P (W^{+} \geq 34)$ .

Figure 16.6 displays the output of two statistical programs. We see from Figure 16.6(a) that the one-sided $P$ -value is $P = 0.1016$ . JMP reports a statistic $S$ as being 11.5. This is simply the difference between $W^{+}$ and $μ_{W^{+}}$ . This small sample does not give convincing evidence of vitamin loss.

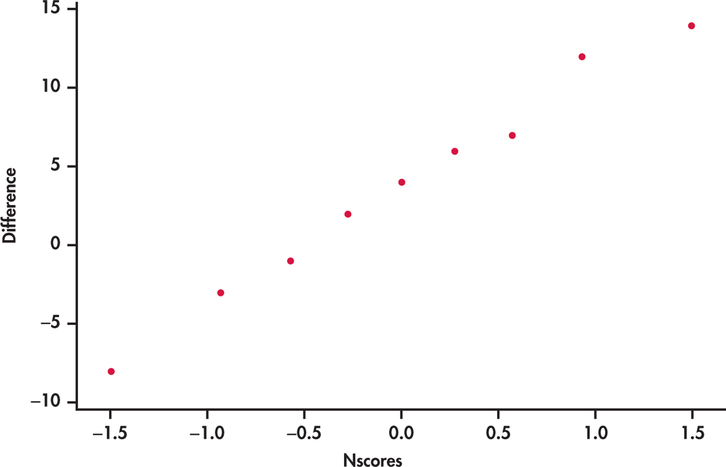
In fact, the Normal quantile plot in Figure 16.7 shows that the differences are reasonably Normal. We could use the paired-sample $t$ to get a similar conclusion ( $t = 1.5595$ , $df = 8$ , $P = 0.0787$ ). The $t$ test has a slightly lower $P$ -value because it is somewhat more powerful than the rank test when the data are actually Normal.

Page 16-18

FIGURE 16.6 Output from (a) JMP and (b) Minitab for the loss of product value study of Example 16.6. JMP reports the exact one-sided

$P$ -value,

$P = 0.1016$ . Minitab uses the Normal approximation with the continuity correction and so gives an approximate one-sided

$P$ -value,

$P = 0.096$ .

FIGURE 16.7 Normal quantile plot of the differences in loss of product value, Example 16.7.