Example 4.31

EXAMPLE 4.31 Applying the Law of Large Numbers

CASE 4.1 With a clipboard, we begin our sampling. The first randomly drawn financial statement entry has an 8 as its first digit. Thus, the initial sample mean is 8. We proceed to select a second financial statement entry, and find the first digit to be 3, so for the mean is now

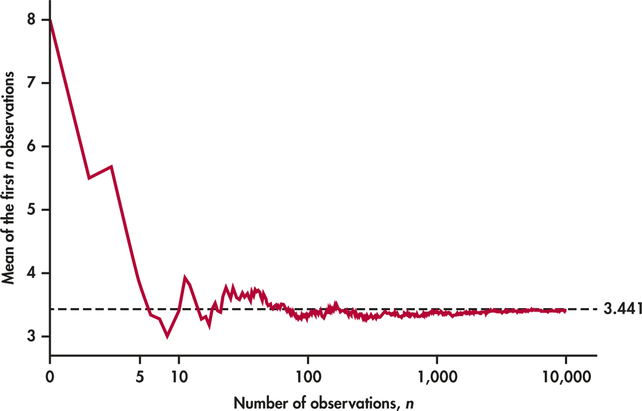
As this stage, we might be tempted to think that digits are equally likely because we have observed a large and a small digit. The flaw in this thinking is obvious. We are believing that short-run results accurately reflect long-run behavior. With clear mind, we proceed to collect more observations and continue to update the sample mean. Figure 4.17 shows that the sample mean changes as we increase the sample size. Notice that the first point is 8 and the second point is the previously calculated mean of 5.5. More importantly, notice that the mean of the observations gets close to the distribution mean and settles down to that value. The law of large numbers says that this always happens.

223

Figure 4.17: FIGURE 4.17 The law of large numbers in action. As we take more observations, the sample mean always approaches the mean (μ) of the population.